水下航行体舱段结构声学设计模型分析

艾海峰陈志坚王 路

1海军工程大学船舶与动力学院,湖北武汉430033

2海军装备研究院舰船论证研究所,北京100161

水下航行体舱段结构声学设计模型分析

艾海峰1陈志坚1王 路2

1海军工程大学船舶与动力学院,湖北武汉430033

2海军装备研究院舰船论证研究所,北京100161

采用基于模态坐标的有限元/边界元方法,建立水下航行体封闭舱段声学设计模型,利用该耦合分析模型对两端采用刚性圆板封闭的简支舱段结构的振声性能进行分析,并与采用半无限长圆柱形刚性障板代替两端的刚性圆板时的舱段模型计算结果作比较,指出除了少数耦合模态的固有频率附近,当外层圆柱壳周长相对流体中声波波长较小时,采用刚性圆板封闭的两端简支双层加筋圆柱壳与两端采用半无限长圆柱形刚性障板代替刚性圆板时的声辐射规律十分相近。

舱段；有限元/边界元；双层加筋圆柱壳；声辐射

1 引言

目前,对水下航行体结构的声学性能设计多是以单一的、较小的和典型的结构单元及构件为对象进行讨论,如板、单层圆柱壳、基座等［1］。这些方法用于设计与控制水下航行体总体声学性能需有一个复杂的转换过程与算法,在实际工程设计中应用颇为不便。水下航行体一般是由若干个舱段所组成,有双壳体结构舱段、亦有单壳体结构舱段,若以舱段为单元进行水下航行体的声学性能设计,将便于控制与分析其总体声学性能。对舱段结构声学性能的研究,目前多采用两端封闭［2-5］和两端带有刚性圆柱形障板［6-9］的圆柱壳结构进行分析,但两端封闭和两端带有刚性圆柱形障板的有限长圆柱壳流固耦合模型在指导舱段结构声学设计时的一致性仍不十分明确。本文首先建立两端封闭舱段结构声学设计模型,采用基于模态坐标的有限元/边界元方法对其耦合振声规律进行研究,将其外表面平均速度和辐射效率同利用文献［8］中解析方法计算半无限长圆柱形刚性障板代替两端封闭圆板的舱段声学模型的结果进行了比较,供水下航行体声学设计参考。

2 封闭舱段结构的声学设计模型

水下航行体的典型舱段模型如图1所示,为两端带有舱壁的双层加筋圆柱壳,其外层壳体设有纵骨,内层壳体采用环筋加强,双层壳体之间为实肋板连接。

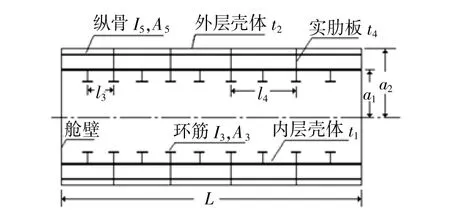
图1 双层加筋封闭舱段结构

将浸没于无限大水域中的双层加筋封闭舱段结构进行有单元离散,划分成个单元和个节点,其结构总体运动方程可写为：

式中,［K］为结构刚度矩阵；［C］为结构阻尼矩阵；［M］为结构质量矩阵{u}为节点位移向量；{Fs}为作用于结构上的外力；{Ff}为结构周围流体对它的作用力；ω为结构振动圆频率。

设结构的节点位移可以采用模态叠加法表示为：

将式(2)代入式(1),并进行正则化处理可得：

由于周围的流体对结构的作用力为：

式中,［L］是结构表面法向向量的变换矩阵,［L］-1为它的逆变换矩阵；{p}为外表面上的节点声压。

将式(4)代入式(3)可得：

式中,［D］=［Ψ］t［L］-1为几何耦合矩阵。

对于外场问题,结构声辐射的边界积分方程为：

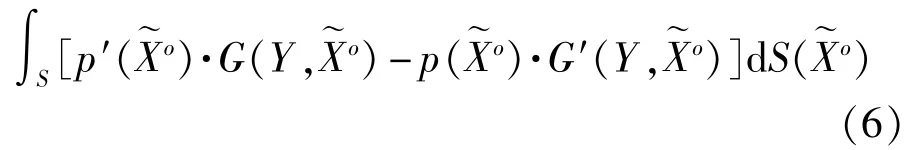
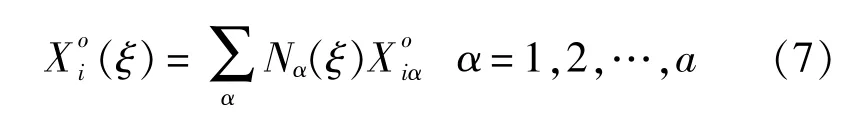
其中,Nα(ξ)为单元插值函数,它是局部坐标ξ (-1≤ξ≤1)的二次函数,对于正方形等参元ξ= (ξ1,ξ2),取为8；对于等边三角形等参面单元 ξ= (ξ1,ξ2,ξ3)且ξ3=1-ξ1-ξ2,取为6,相应的插值函数Nα(ξ)参见文献［10］。

在全局单元编号为m~的外表面单元上,同样利用Nα(ξ)对边界声学变量p、p'进行插值,对于单元内任意点ξ有：

式中,

由式(10)可以形成关于外表面单元节点未知量p和p'的联立代数方程组,将其采用矩阵形式可以写为：

其中,矩阵［A］和［B］中的元素可以通过式(10)得到。

结构外表面上的未知量可以通过求解式(11)获得。为了得到精确的求解结果,必须要精确计算式(11)中的单元系数矩阵［A］和［B］,将单元的系数写为如下积分形式：

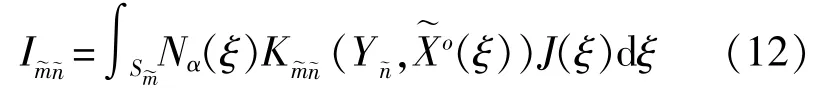
在结构外表面上,声压与结构位移的关系为：

式中,ρ0为流体密度。

将式(2)与式(13)代入式(11)可得模态坐标下边界元声学方程为：

联立式(5)、式(14),在无其它入射场的情况下,可得基于模态叠加的结构流固耦合振动方程为：

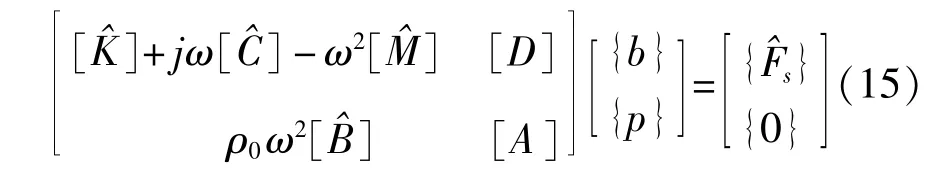
求解式(15)即可得结构振的模态主坐标和外表面的节点声压,则利用结构位移的模态叠加表示法以及式(6)则可得到结构上任意一点的振动位移以及空间外场内任一点的辐射声压。

舱段结构外表面的法向面平均速度级为：

结构的辐射效率级可表示为：

3 舱段结构声学模型的耦合振声分析比较

封闭舱段结构的外壳长度半径比为L/a2= 2.91,内壳厚度半径比为t1/a1=9.13×10-3,a1/a2= 0.84,t1/t2=7,肋骨间距与实肋板间距之比为l3/ l4=0.5,外壳厚度与实肋板厚度之比为t2/t4= 0.75,等间距环筋的惯性距截面积比为I3/A3= 2.02×10-3,l3/L=0.1,t1L/A3=8.75×10-3,等间距纵骨的惯性距比为I5/A5=9.59×10-4,A3/A5=6.64,角间距为30°,材料的弹性模量为E=2.1×1011Pa,泊松比σ=0.3,材料损耗因子η=0.001,密度ρ=7.8×103kg/m3,舱段结构外部流体中的声速为c0=1.56×103m/s,密度为ρ0=1.025×103kg/m3。舱段两端为简支边界条件,并采用刚性圆板封闭,单位简谐径向集中点力作用于有限长内层圆柱壳的母线中点处。计算小于外层圆柱壳环频率ωr2(ωr2a2/c0=3.487,对应的外层壳体半径与流体中声波波长比a2/(2πc0/ωr2)为0.555)的低频范围内的声辐射,计算频段为ka2∈［0.004,1.735］,为了获得较为精确的解,在单元划分时,单元的最大尺度小于最高计算频率所对应的波长的1/6,在进行模态截断时,所采用的模态的最高固有频率达到最高计算频率的2倍以上,这里采用有限长圆柱壳的前600阶模态进行叠加计算,也即取Q= 600,最大固有频率对应的无因次频率为ka2= 6.902。

由于综合考虑结构表面振速和辐射效率能够获得结构声辐射性能,为了比较两端封闭和两端带有刚性圆柱形障板的舱段流固耦合模型［8］在结构声学设计时的一致性,设封闭舱段结构的外表面法向面平均速度级和辐射效率级分别为和(计算频段内舱段结构的辐射效率级小于0),则两端带半无限长圆柱形刚性障板的舱段声学模型所计算的外表面法向面平均速度级相对差值δLv和辐射效率级相对差值δLσ可分别定义为：

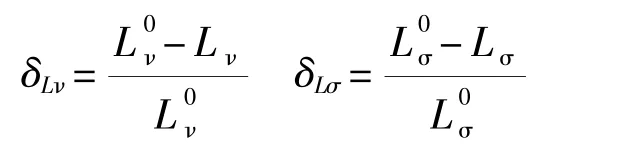
法向面平均速度级相对差值和辐射效率相对差值分别如图2和图3所示,可以看出,当外层圆柱壳半径相对流体中声波波长较小时,对于采用刚性圆板封闭的两端简支双层加筋圆柱壳,考虑流固耦合影响并且用半无限长圆柱形刚性障板代替两端的刚性圆板时的计算结果与直接考虑流固耦合影响的计算结果较为接近,较大的误差发生在少数耦合模态的固有频率附近,当ka2＜1.0时,也即外层圆柱壳周长小于流体中声波波长时,两者法向面平均速度级和辐射效率级的相对差值均在5%以内。

图2 法向面平均速度级的相对差值

4 结束语

图3 辐射效率级的相对差值

在模态坐标下,利用FEM/BEM相结合的方法建立了封闭舱段结构的声学设计模型,该方法可以适用于任意封闭结构在任意边界条件下的耦合振声分析,通过两端简支在半无限长圆柱形刚性障板上舱段声学模型与采用刚性圆板封闭的两端简支舱段声学模型的比较表明,当外层圆柱壳周长相对流体中声波波长较小时,法向面平均速度级和辐射效率级的较大差值只发生在少数耦合模态的固有频率附近,除此之外,利用两端简支在半无限长圆柱形刚性障板上的舱段声学模型研究采用刚性圆板封闭的两端简支舱段结构的声辐射规律是可行的。

［1］ 阿·斯·尼基福诺夫著.船体结构声学设计［M］.谢信,王轲,译.北京：国防工业出版社,1998.

［2］ 商德江,何祚镛.加肋双层圆柱壳振动声辐射数值计算分析［J］.声学学报,2001,26(3)：193-201.

［3］ 陈军明,陈应波,黄玉盈.水中双向正交加肋圆柱壳体声辐射的有限元法 ［J］.武汉理工大学学报,2004,26(4)：74-76.

［4］ 石焕文,盛美萍,孙进才,等.加纵肋平底圆柱壳振动和声辐射的FEM/BEM研究［J］.振动与冲击,2006,25(2)：88-92.

［5］ CHOI S H,IGUSA T,ACHENBACH J D.Acoustic radiation from a finite-length shell with non-axisymmetric substructures using a surface variational principle［J］.Journal of Sound and Vibration,1996,197(3)：329-350.

［6］ 汤渭霖,何兵蓉.水中有限长加肋圆柱壳体振动和声辐射近似解析解［J］.声学学报,2001,26(1)：1-5.

［7］ 文丽,骆东平等.流场中有限长纵横加筋圆柱壳声辐射［J］.华中理工大学学报,1999,27(8)：54-56.

［8］ 陈美霞,骆东平.敷设阻尼材料的双层圆柱壳声辐射性能分析［J］.声学学报,2003,28(6)：486-493.

［9］ 周锋,骆东平,蔡敏波,等.有限长环肋圆柱壳低阶模态声辐射性能分析［J］.应用科技,2004,31(9)：38-41.

［10］杨德全,赵忠生.边界元理论及应用［M］.北京：北京理工大学出版社,2002.

［11］SOENARKO B.An advanced boundary element formulation for acoustic radiation and scattering in three dimensions［D］.Department of Mechanical Engineering,University of Kentucky,Kentucky,1983.

Structural-Acoustic Analysis on the Cabin of Underwater Vehicle

Ai Hai-feng1Chen Zhi-jian1Wang Lu2
1 College of Naval Architecture and Power,Naval University of Engineering,Wuhan 430033,China
2 The Institute of Naval Vessel,Naval Academy of Armament,Beijing 100161,China

The structural-acoustic design model for an enclosed cabin section of underwater vehicle was built up using FEM/BEM method based on modal coordinates,the vibration and sound radiation characteristics were analyzed by this coupled design model for the simple supported finite cylindrical shell ended with rigid circular plates.The results were compared with that of substituting semi-infinite rigid cylindrical baffles for the rigid circular plates.It demonstrates that as the perimeter of the outer cylindrical shell is smaller compared to the wavelength of sound in ambient fluid,the sound radiation law of the simple supported and stiffened double cylindrical shell ended with rigid circular plates is similar with that extended by two semi-infinite length rigid cylindrical baffles,except the case that is near the natural frequencies of a few coupled modes.

cabin；FEM/BEM；stiffened double cylindrical shell；sound radiation

U661.44

A

1673-3185(2010)06-12-04

10.3969/j.issn.1673-3185.2010.06.003

2010-04-09

国防“十一五”预研项目(4011101020101)

艾海峰(1983-),男,博士研究生。研究方向：舰船声隐身技术。E-mail：aihaifeng_123@163.com

陈志坚(1957-),男,教授,博士生导师。研究方向：舰艇结构强度设计及其声隐身技术。

E-mail：chengliu1957@yahoo.com.cn