中国区域相对价格水平收敛性实证研究

苏芳,蔡经汉,王世杰

(1.华侨大学数量经济研究院,福建 泉州 362021;2.华东交通大学 经济管理学院,江西 南昌 330013)

一国范围内区域相对价格水平收敛问题近年来成为文献的研究热点。价格水平的高度离散性及其持续时间不但对各个区域的工资率和生活水平具有重要的政策含义,同时还关系到资源配置的有效性。如果各个区域实行单一货币或者没有明显的要素流动约束,那么价格水平离散性就可能意味着区域商品市场存在分割,因此,系统性的价格水平离散性对于政策制定者来说无疑是一个很大的挑战。

区域价格水平收敛是在汇率的一价定律(Law of One Price)基础上提出的。购买力平价理论认为,根据一价定律原则,两国价格水平差别是暂时的,套利行为会使得这种差别逐渐消失,即实际汇率时间序列是平稳的。基于这种思想,考察一国内部区域之间是否存在价格水平收敛,可以通过检验其相对价格水平是否具有单位根而进行。在早期单变量的单位根检验中,由于时间序列样本容量较小缘故,检验结果往往倾向于接受序列具有单位根的假设。增加时间序列样本容量虽然能部分解决检验势较低的问题,但是较长时间序列样本区间可能存在结构变化的问题。因此,最新文献一般都建议采用面板数据单位根检验方法以提高检验的势。这些国内外研究包括Parsley和Wei(1996)[1]、Ceccetti et al.(2002)[2]、Ceglowski(2003)[3]、鄂永健(2007)[4]、Rizki(2009)[5]、Chmelarova和 Nath(2009)[6]等 。

由于我国施行单一货币,而且改革开放以来我国区域生产要素流动限制已大为减弱,这些因素导致商品价格水平在我国不同地区将同时相关;同时由于我国幅员辽阔,区域不同气候条件与区域经济发展存在差异性,价格水平也会受到区域特有的冲击,价格水平可能呈现一定的离散度。由此我们提出的问题是:随着改革开放的深入,我国已逐步融入世界经济一体化进程,然而改革开放是否也使得内部区域市场整合更为紧密?区域间价格水平差异是发散还是收敛的?如果是收敛,那么收敛速度有多快?更深层次的问题是:东、中、西部内部地区市场整合速度是否呈现与全国类似的特点。即在上述3个差异性较少的东、中、西部区域其价格水平是否收敛?如果收敛,是否由于内部差异性相对于全国更小,而呈现更快的收敛速度?各类具体的商品价格指数收敛性又有什么异同?为回答上述问题,本文拟采用多种面板单位根检验方法研究我国区域价格水平收敛现象。与国内外研究不同的是,本文控制了“基年价格指数”的问题,而且第一代和第二代多种面板单位根检验方法的结论相互验证,增强了结论的可信性和稳健性。考虑到我国地域辽阔,我们在全国样本检验基础上,继续把全国样本分为东、中、西部3个子样本,对3个子样本的检验结果进行收敛速度比较,以发现三大区域是否与全国保持大致相同的市场整合速度。此外还比较了CPI中八大分类价格指数的收敛速度。地区间价格水平差距及其持续时间长短是衡量国内市场一体化程度的标志,本文研究区域相对价格水平收敛性可为政府制定缩小市场分割,提高市场整合程度的政策提供理论支持。

本文结构安排如下:第二部分介绍本文使用的检验方法;第三部分是实证分析,首先给出样本数据,其次报告面板单位根检验结果以及收敛速度估计结果;最后一部分是总结。

1 面板单位根检验方法

本部分对本文所应用的面板单位根检验方法作简单介绍。考虑如下形式的ADF检验式

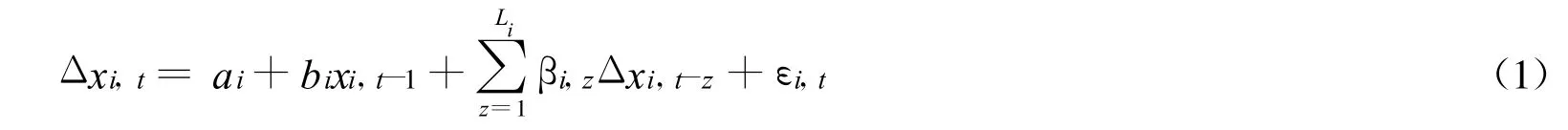
其中,xi,t表示解释变量,Δxi,t表示解释变量的阶差分,t-1表示滞后1期,t-z表示滞后2期,ε为残差,ai,bi,βi为等估计参数,bi=ρi-1ρi表示单位根,假设 ρi=1就意味着bi=0,i=1,2,…,N,t=1,2,…,T。

Levin,Lin和Chu(2002)[7]提出LLC检验,其考虑的模型假设其中面板中各单元的自回归参数都是相同的,即bi=b。因此,ADF模型即简化为

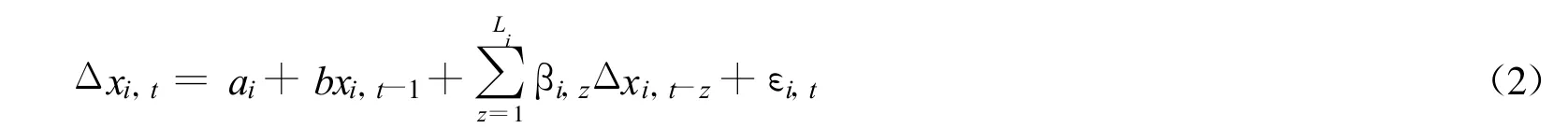
LLC检验虽然仍采用ADF检验式形式,但并没有直接使用Δxi,t和xi,t-1对参数b进行估计,而是使用Δxi,t和xi,t-1的代理变量去估计参数b,其所获得的与参数b相对应的t统计量渐近服从标准正态分布。Hadri(2000)[8]提出的Hadri检验虽然与LLC检验一样都是假设面板数据中的各截面序列都具有相同的单位根过程,即假定bi=b,但其采用的是与KPSS检验相类似的原假设,即从平稳性出发来进行假设检验。

Madadla和Wu(1999)[9]指出,LLC检验等使用的同质性假设过于严格,并且容易出现固定效应估计量的同质性偏误问题。对此,包括Im,Pesaran和Shin(2003)[10]提出的IPS检验采用了异质性假设,即允许参数bi跨截面变化,各截面序列具有不同的单位根过程。其中,IPS检验与LLC检验同样采取ADF检验式,但首先对每个截面成员进行单位根检验,得到每个截面成员bi的t统计量后取平均值而构造出检验整个面板数据是否存在单位根的t-bar统计量。而Madadla和Wu(1999)[9]则提出非参数Fisher类型检验,这种非参类型的检验在一定程度上克服了基于ADF框的LLC或IPS检验存在的一些缺点。

第一代面板单位根检验方法都假定面板数据中各截面互不相关,这样的假定使得检验变得简单。但现实中,这一假定很难成立。在现实经济运行中,许多可观测或不可观测的共同因子都将导致截面相关性的存在。例如,经济周期对各截面单元存在共同的冲击,而空间溢出效应也可能导致不同截面单元之间存在相关关系。对同处一国境内的诸省级单元来说,国家的政策变量显然也是一个共同因子。尽管同一项政策可能对不同省份产生的影响有大有小,但由此仍然导致了不同程度的截面相关性。此外,从理论上说,截面相关性的存在会影响面板单位根估计的有限样本性质。因此,只使用第一代方法是不够的,为了提高检验的可靠性和结论的稳健性,必须结合第二代方法进行检验。

在使用第二代方法之前,首先要对截面相关性进行检验。对此,Breusch和Pagan(1980)[11]提出LM检验。本文将同时使用这两种方法及LM检验的一个比例化版本:SCLM检验。各检验统计量如下其中为第i个截面单位作OLS回归所得残差。T表示自回归所得T统计量值。

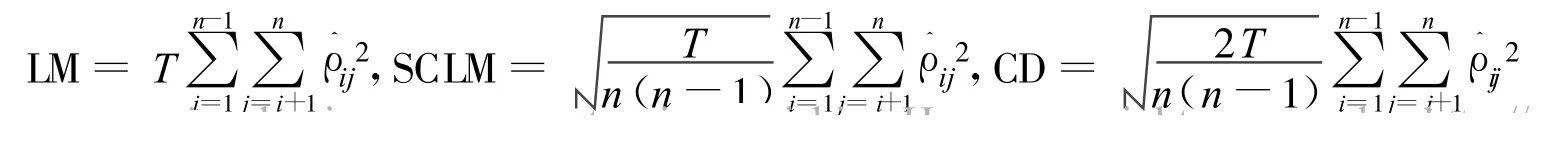
在确认截面相关性的存在后,本文将使用Pesaran(2007)[12]所提出的第二代面板单位根检验的CADF方法。该方法扩展了存在截面相关时的标准ADF回归式(为简便计,以下仅考虑滞后一阶的情况)其中,与标准ADF检验不同的是在式(3)中包含了截面平均以其作为共同因子的代理变量。

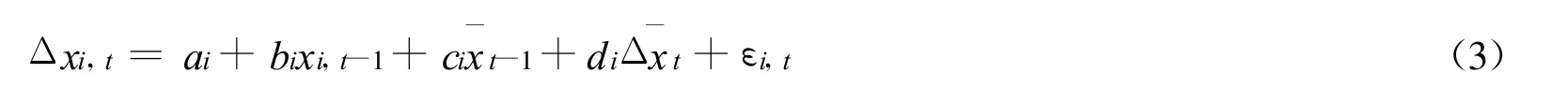
2 实证结果与分析

2.1 样本数据与处理

本文选取1985—2008年我国28个省级区域(因为数据不全,故不包括西藏、重庆、青海)的年度居民消费价格指数(CPI)进行检验,数据来源于中国经济信息网数据库。所有地区的CPI均调整为以1984年为100,省级区域i的价格水平记为pi。为计算相对价格水平,我们选取北京为基准地区,那么地区i与北京市j的相对价格水平则为:qit=ln(pit/pjt)。为简化篇幅便于比较,图1只给出了山东、湖北和四川相对价格水平对数的序列。从图1可以看到,3个省的相对价格水平对数均小于零,这说明北京市的价格水平高于这3个地区。但是,3个地区的相对价格水平都显示出具有共同的变化趋势。这意味着从长期来看,虽然地区间价格水平有差异,但它们可能存在一个共同的收敛趋势。究竟相对价格水平是发散还是收敛,这需要采用计量模型进行验证。

Philips和Sul(2007)[13]提出所谓的“基年价格指数”问题,他们在研究中举例说,如以1918年为基年,则1918年当年各地价格指数相同(都为100),那么相对价格水平就无法比较。为此,在他们的研究中,从1918—2000年的总样本中舍弃了1918—1959年的样本。为了避免“基年价格初始化”问题,借鉴Philips和Sul(2007)[14]的做法,本文首先舍弃掉1985—1995年间的样本数据,仅使用1996—2008年样本数据进行单位根检验。

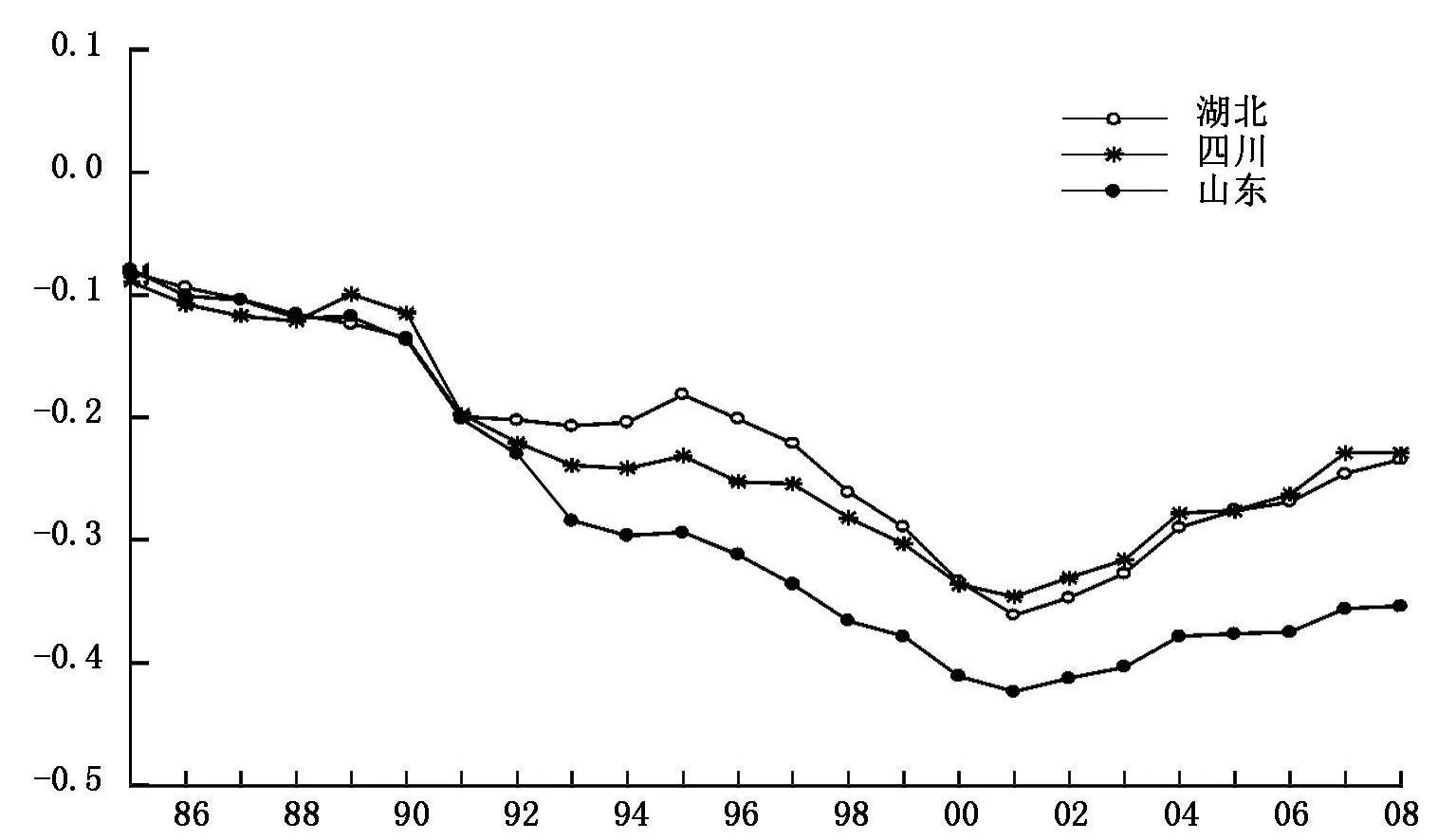
图1 山东、湖北、四川的相对价格水平对数变化趋势

2.2 面板单位根检验结果

本部分首先使用上述各种面板单位根检验方法对全国样本进行检验,而后将全国样本分为东、中、西部3个子样本分别进行检验,各序列的最优滞后期数依据BIC最小的准则。检验结果列在表1中。

从表1的检验结果,本文有如下结论:

首先,从全国样本的检验结果看,LLC、IPS、Fisher-ADF、Fisher-PP这4种检验方法均在5%水平下拒绝单位根的零假设,而Hadri检验结果则表明,在5%显著性水平下不能拒绝序列是平稳的零假设。因此上述各种面板数据单位根检验结果说明,在我国国内市场中,以北京市作为基准的其他各省份的相对价格指数对数不是单位根过程,而是具有平稳性的序列,这表明一价定律在我国国内市场基本上成立的。

表1 面板单位根检验结果

其次,从3个子样本的检验结果看,东部及中部均是收敛的,而西部存在单位根的结论。

西部样本的检验结果中LLC检验的结论虽然拒绝了零假设,但是,我们注意到,LLC的零假设是所有截面序列都存在相同的单位根,而其备择假设是均没有单位根。这一同质性假设在Maddala和Wu(1999)[9]文中已受到批评,结合IPS检验的结果来看,这可能说明各截面序列具有不同单位根。而其余3种检验的结果进一步加强了价格水平发散的结论。这表明,与东、中部相比,西部地区还存在一定程度的市场分割。

第三,上述检验结果具有稳健性。本文将整个样本区间划分为1996—2001年和2002—2008年两个子区间,继续应用上述检验方法,在第一个样本区间,除IPS检验法无法拒绝单位根存在,其余几个都拒绝单位根原假设。而对于第二个样本区间,除Fish-PP检验外,均一致认为相对价格水平对数序列是平稳序列。

2.3 收敛速度估计

前述部分研究结果证明我国区域相对价格水平存在收敛性,但是就全国样本而言,这种收敛的速度有多快?而在东、中、西部三大地带,相对价格水平收敛速度是否与全国保持同步,或者它们之间收敛速度也具有差异性?本部分利用LLC面板单位根检验结果中计算得到的自回归参数b^,进一步由半衰期计算公式为:-ln 2/ln(ρ^),其中ρ^=1+b^。由此得到度量相对价格水平收敛的速度。同样地将样本分为东、中、西部,然而西部样本检验结果表明价格水平是发散的,因此半衰期不予计算。计算结果列在表2中。

表2 收敛速度

为得到收敛速度的变化,而反映我国区域市场整合动态进程,我们分别对样本区间1996—2000年、1996—2001年、……、1996—2008年等7个样本区间进行面板单位根检验与收敛速度计算,面板单位根检验结果显示,在5%水平下,序列均为平稳的序列。而由此进一步得到的7个收敛速度,其变化趋势见图2。从图2可以发现,随着样本越靠近现在,半衰期逐步下降,这表明价格水平的收敛速度越来越快,我国内部市场整合程度越来越好,市场一体化程度越来越高,市场分割现象已逐步减弱,市场经济正在逐步完善。

CPI是一种综合性指数,由食品、衣着等八大类商品指数构成。一方面,从理论上说,由综合价格指数所计算得到的收敛速度一般由收敛速度最慢的分类商品价格指数所决定,个类商品价格指数的收敛速度存在差异性,如果仅考察综合价格水平指数,那就有可能忽视各个个体之间的差异性。另一方面,分析具体商品指数的收敛速度,可以发现哪些类别商品存在市场分割,这可为政府制定促进具体商品的市场整合政策提供理论支持。各类商品价格指数收敛速度具体计算结果列在表3中。

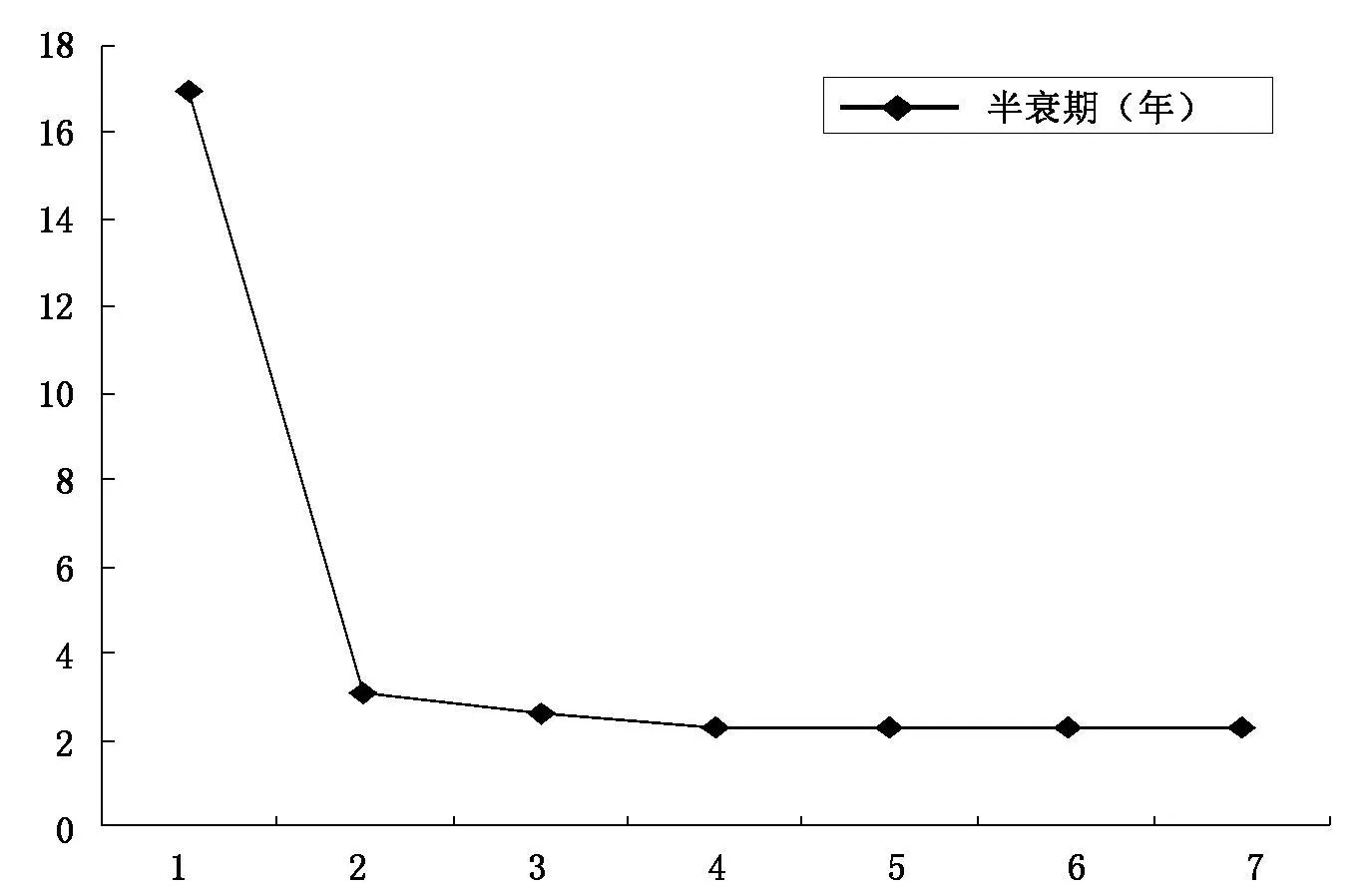
图2 收敛速度变化趋势

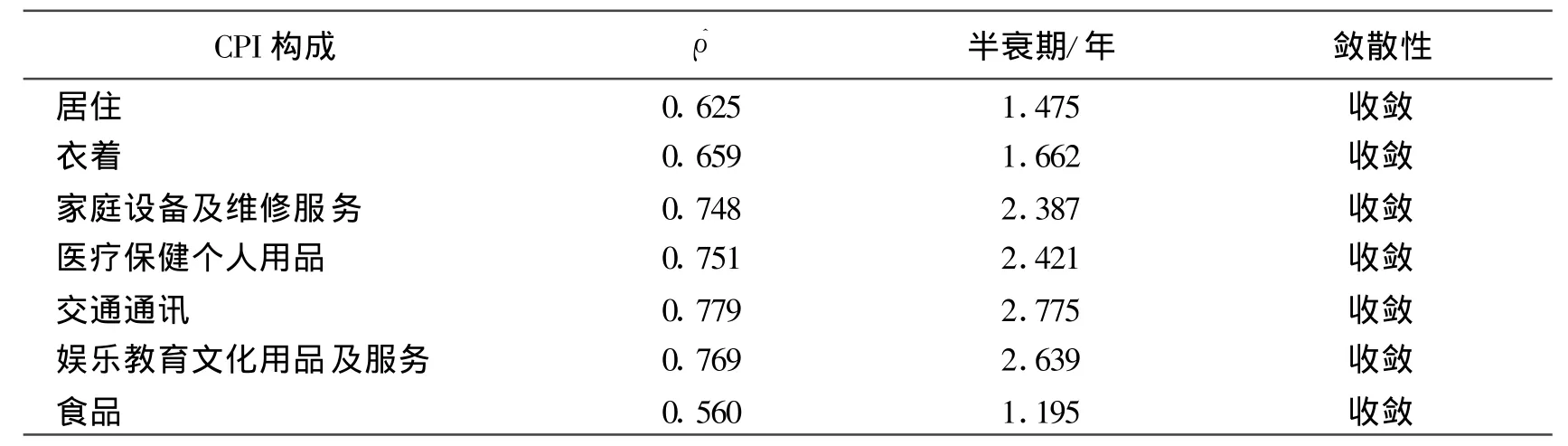
表3 分类商品价格指数收敛性与半衰期

2.4 截面相关性检验与第二代面板单位根检验

第一代面板单位检验中截面单位相互独立是一个严格却未必符合实际的假定,实际存在的截面相关关系可能导致第一代面板单位检验结论出现显著偏差。有鉴于此,为了保证结论的可靠性,本文采用CD、LM、SCLM等截面相关检验方法对截面单位之间是否存在显著的相关关系进行检验,如果能检验出截面相关,则在此基础上进一步应用第二代面板单位根检验。最后的检验结果列在表4,表5中。在截面相关检验部分,本文发现,无论是全国样本或者是东中西部各子样本,各种截面相关检验的统计量均在1%的显著水平下拒绝了截面单位相互独立的零假设,这就意味着由于经济政策、单一货币因素等可观察或不可观察的共同因子的影响,我国各区域商品价格之间存在着显著的相关关系。因此,为了克服检验过程中的截面相关性问题并保证结论的可靠性,结合最新的研究进展,本文采用考虑截面单位相互依赖的面板数据单位根检验方法——CADF检验法,以对我国是否区域相对价格收敛性展开进一步的深入分析。表5结果表明,第二代单位根检验结果基本与第一代面板单位根检验结论相同。因此,本文所考察样本期间内,我国区域相对价格收敛性检验结果具有较强的稳健性。

表4 截面相关检验结果

表5 第二代面板单位根检验(CADF检验)结果

3 结论

基于1996—2008年我国29个省级区域消费价格指数面板数据,本文在现有第一代面板单位根检验的基础上结合新近发展的第二代面板单位根检验方法,对我国区域相对价格水平收敛性进行深入的实证分析。结果发现,全国范围内的价格水平虽然存在差异性,但存在共同的变化趋势。而在东、中、西部的区域内部价格水平收敛性各不相同,东中部由于市场经济相对比西部成熟,内部市场整合程度较高,而西部一定程度上还存在市场分割。在具体商品分类指数的收敛性方面,食品类商品收敛速度最快,而交通通讯、娱乐教育等商品价格指数收敛速度最慢。

[1]PARSLEY D,WEI S.Convergence to the law of one price without trade barriers or currency fluctuations[J].Quarterly Journal of Economics,1996(4):1 211-1 236.

[2]CECCHETTI S G,MARK N C,SONOR A R J.Price index convergence among United States cities[J].International Economic Review,2002(2):1 081-1 099.

[3]CEGLOWSKI J.The law of one price:intranational evidence for Canada.Candian[J].Journal of Economics 2003(36):373-400.

[4]鄂永健.中国地区间价格水平差距趋于收敛还是发散[J].经济评论,2007(5):113-117.

[5]RIZKI E.Wimanda Price variability and price convergence:Evidence fromIndonesia[J].Journal of Asian Economics,2009(20):427-442.

[6]VIER A C,HIR ANYA K.N.Relative price convergence among US cities:Doesthe choice of numeraire city matter?[J].Forthcoming in Journal of Macroeconomics 2009(3):45-57.

[7]LEVIN A,LIN C,CHU C.Unit root tests in panel data:asymptotic and finite-sample properties[J].Journal of Econometrics,2002(108):1-24.

[8]HARDI K.Testing for stationarity inHeterogeneous Panel Data[J].Econometric Journal,2000(2):148-161.

[9]MADDALA G S,WU S A comparative study of unit root testswith panel data and a new simple test[J].Oxford Bulletin of Economics and Statistics,1999(61):631-52.

[10]IM K S,PESARAN M H,SHIN Y.Testing for unit roots in heterogeneous panels[J].Journal of Econometrics,2003(115):53-74.

[11]BREUSCH T,PAGAN A.The Lagrange Multiplier Test and ItsApplications to ModelSpecification in Econometrics[J].Review of Economic Studies,1980(47):239-253.

[12]PESARAN M H.A Simple Panel Unit Root Test in the Presence of Cross Section Dependence[J].Journal of Applied Econometrics,2007(22):265-312.

[13]PHILLIPS P C B,SUL D.Transition modelling and econometric convergence tests[J].Econometrica,2007(6):1771-1855.