分析测试中取样单元数的确定——关于分析化学教材中取样问题的商榷

赵中一 金继红

(中国地质大学(武汉)材料科学与化学工程学院 湖北武汉430074)

分析测试中取样单元数的确定
——关于分析化学教材中取样问题的商榷

赵中一 金继红

(中国地质大学(武汉)材料科学与化学工程学院 湖北武汉430074)

对武汉大学主编的《分析化学》(上册)第5版教材中关于取样单元数的计算进行了讨论，指出测量次数与采样单元数是不同的概念，在已知采样单元间的标准偏差估计值和允许误差的情况下，采样单元数应该用试差法求得。

武汉大学主编的第5版《分析化学》(上册)［1］是“高等教育面向21世纪课程教材”，也是高等教育出版社百门精品课程教材之一。该教材自1978年初版问世至今，已再版多次，是一本应用广泛的优秀教材。第5版(上册)在原有版本的基础上进行了内容修订和章节调整。其中关于固体试样采样单元数的有关内容是新增加的内容之一。

正如该教材中指出，试样的采集是分析工作中的重要环节，它们直接影响试样的代表性、分析结果的可靠性及分析测试工作的成本。但目前涉及此部分内容的分析化学教材甚少，故该教材中增加这部分内容是很必要的。但我们在教学实践中发现，该教材第2章(分析试样的采集与制备)中对于固体试样采样单元数的阐述有值得商榷之处，现对其中的问题进行探讨。

分析化学的全过程是将原始分析对象通过“采样”收集在样品中，然后经“测量”取得分析结果，再通过“数据处理”反映该分析对象的信息。分析结果的误差主要是由采样误差与测量误差两部分决定。若测量误差很小时，则分析结果的误差仅由采样引起。在简单随机抽样试验中，若质量特征值x遵从正态分布N(μ，σ2)，在有限次测定中，x遵从t分布，可通过下式，用样本的平均值¯x估计总体平均值μ。

式(1)中，μ为总体平均值，s为样本的标准偏差，t为一定置信度与自由度时的t统计量，n为采样单元数。设总体平均值与抽样样本的平均值的差为E，E=μ－¯x，由式(1)可得计算采样数n的公式为:

从式(2)可知:只要知道了t，就能求出n，但要知道t，必须先知道n。解决这个矛盾可用“试差法”，即先假设一个取样数n，从t分布表中查得在一定置信度时的t值，将此t值代入式(2)中计算出一个新的n，然后用此n再查得一个新的t值。如此循环，直到前后两次求得的n值相等或相接近为止。从t分布表可知，当n＞30时，t0.05，30≈2，文献［2］建议先用t=2代入式(2)中计算出n，然后再进行循环。若计算出的n小于5，则取n=5，再用“试差法”来确定n值。取值时n一般不要小于5。也有文献介绍，可先用n=∞作为自由度来确定t值，不断循环计算，直到n收敛于一常数［3］。

武汉大学主编的第5版《分析化学》(上册)教材在介绍这部分内容时，有以下几方面不妥:

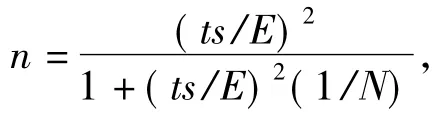
③教材将测量次数混同于采样数。在25页11行中提到“若增加试样的测定次数，则t值变小，采样单元数相应减少”。为了说明增加测定次数可以减少采样数，教材还举例说，如果测定4次，应从5个不同的采样点分别采集一份试样，若测定次数增加到10次，即只需从3个不同的采样点分别采集一份试样。照教材的计算方法，不论样品均匀程度如何，只要测定次数增加，取样数都可减少，这是不正确的。在教材中将重复测量次数n混同于采样数，依据重复测量次数n查找t值是不妥的。若已知n值，又何必再求n值呢?教材中实例的计算方法会使读者感到困惑，若按照此方法对本章习题进行解答，会得到错误答案。

以下通过求解教材37页习题1来具体说明确定采样单元数的方法［4］。

题目:某种物料，如各个采样单元间标准偏差的估计值为0.61%，允许的误差为0.48%，测定8次，置信水平选定为90%，则采样单元数应为多少?

解:用“试差法”来估计采样单元数n。先用n=∞时的tα，∞，由式(2)计算出一个n值;再用此n值查得一个新的t值，再计算出一个n;如此循环，直到计算出的n趋于常数。若计算出的n小于5，则取n=5，再用“尝试法”来确定n值。

置信水平为0.90、n=∞时，t=1.64，按式(2)可得:

计算的n值与前次设定的n=6接近，所以采样单元数为6。

［1］ 武汉大学.分析化学(上册).第5版.北京:高等教育出版社，2006

［2］ 邓勃.分析测试数据的统计处理方法.北京:清华大学出版社，1995

［3］ 梁逸曾，俞汝勤.分析化学手册第10分册化学计量学.第2版.北京:化学工业出版社，2000

［4］ 赵中一，邱海鸥.分析化学辅导与习题详解.武汉:华中科技大学出版社，2008