能量分解法在羰基配合物成键本质研究中的应用*
2010-07-02王斌举夏文生张俊万惠霖
王斌举 夏文生张俊 万惠霖
(厦门大学化学化工学院固体表面物理化学国家重点实验室 福建厦门361005)
师生笔谈
能量分解法在羰基配合物成键本质研究中的应用*
王斌举 夏文生**张俊 万惠霖
(厦门大学化学化工学院固体表面物理化学国家重点实验室 福建厦门361005)
借助量子化学能量分解法的思想,以对Cr(CO)6及TMq(CO)6(TMq=Hf2-,Ta-,W,Re+,Os2+,Ir3+)中金属-羰基的成键中能量贡献的分解分析为例,对金属-羰基成键中不同类型的相互作用和成键本质进行了分析和总结,并与人们传统的认识进行了比较。
CO在金属表面上的化学吸附,及CO与过渡金属间的配位成键,均为实验和理论研究的热点,但有关CO-金属的成键本质,直至量子计算化学理论以及计算机速度有了长足的发展之后,人们才有了一定的认识。本文主要基于G.Frenking和N.Frohlich的一篇综述性文章(Chem Rev,2000,100(2):717-774),介绍最近有关羰基配合物中的成键的理论研究成果,即通过能量分解法对金属羰基配合物中羰基-金属的成键本质进行研究所获得的认知。
1 CO与金属成键的基本认识
CO的电子排布方式可表示为:(1σ)2(2σ)2(3σ)2(4σ)2(1π)4(5σ)2(2π*)0,前线轨道HOMO和LUMO分别是5σ和2π*。对于CO的5σ轨道,其主要由O的孤对电子反馈到C上形成,致使C端带有更多负电荷,因而CO作为电子供体时C的反应活性大于O;对于CO的2π*轨道,由于O的电负性大于C,相应O的2p原子轨道能量低于C的2p原子轨道,当原子轨道组合成分子轨道时,致使成键轨道1π含更多O的成分,反键轨道2π*含更多C的成分,因而CO作为电子受体时C的反应活性也大于O。
如图1所示,按前线轨道理论,CO与金属相互作用形成σ键和π反馈键,其相互作用体系能态密度分布情况示于图2[1]。不难看出,CO的5σ轨道和2π*轨道各自与金属的作用将分别导致新的成键和反键轨道。
图2表明,成键轨道对应能量相对较低的峰(与5σ、2π*各自分别相关的两个峰中能量较低的峰),而反键轨道对应能量较高的峰。由于费米能级εF几乎位于5σ与金属形成的反键轨道的顶部,故5σ与金属间的相互作用产生弱的成键作用,而费米能级εF位于2π*与金属形成的成键轨道的中部,所以其作用可视为强成键作用。因此,通常情况下CO与金属间成键作用的主要贡献应来自于CO的2π*轨道,即金属(M)向CO的电子反馈。由此可以推测,金属所带负电荷愈多,金属的反馈能力应愈强,故M—CO键也应愈强。
然而,这一认识与最近的理论研究结果并非一致。图3所示为六羰基配位化合物TMq(CO)6(TMq=Hf2-,Ta-,W,Re+,Os2+,Ir3+)中的C—O键长和第一CO配体解离能(断M—CO键所需能量)与不同金属相关联的密度泛函理论研究结果[2]。其中,C—O键长值随第三过渡系金属(Hf2-到Ir3+)自左到右而逐渐减小(单调变化),其原因应为金属向CO的2π*轨道反馈电子使C—O键削弱,反馈电子愈多,C—O键削弱程度则愈大,C—O键长越长。对O—C—M而言,C—O键削弱的同时,M—CO键则似乎应得到增强,然而,第一CO配体解离能的大小随金属所带电荷的变化却呈U形变化(并非所期待的单调变化)。因此,M—CO键的强弱与金属所带电荷或向CO的2π*轨道反馈电子的多少之间并不存在简单的关联,说明上述有关金属—CO的成键的传统认识存在一定的局限性。

图1 CO与过渡金属间的σ键和π反馈键
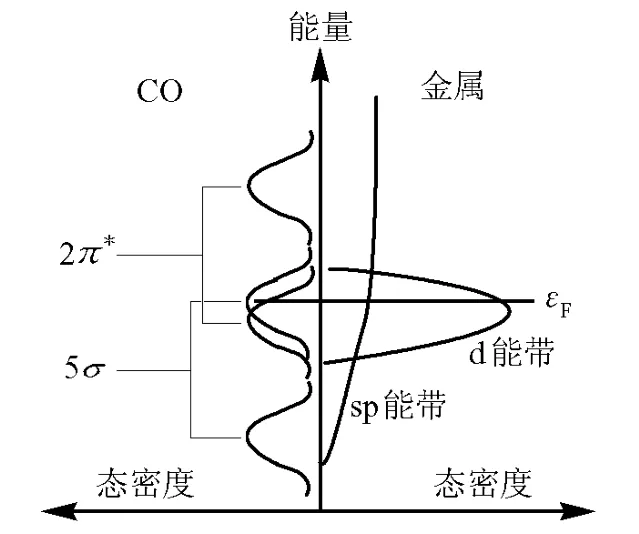
图2 CO与金属作用时体系能态密度分布

图3 DFT计算的C—O键长和第一CO配体解离能变化趋势
2 M orokuma能量分解法
按照Morokuma[3]能量分解法的思想,化学键键能可想象为由几个不同过程或部分的贡献组成。A-B键的总键能ΔE可分解表示为:ΔE=ΔEprep+ΔEels+ΔEPauli+ΔEorb,其中ΔEprep是将A和B从各自的平衡几何构型和电子基态“激发”到化合物AB中的几何构型和电子态时所需要的能量;ΔEels是电子分布被冻结的AB化合物中A、B间的静电相互作用能(通常是吸引性的);ΔEPauli为占据轨道中自旋相同电子靠近时的相关作用能,即Pauli排斥能;ΔEorb为A、B中对称性匹配的前线轨道间的相互作用,即轨道相互作用能,能进一步分解为不同对称性轨道作用(如σ和π)的贡献部分。
3 M orokuma能量分解法对羰基配合物中金属-羰基键的成键本质的认识
3.1 Cr(CO)6的能量分解分析
对金属和羰基配合物中的成键的最深入彻底的研究是由Davidson小组[4-5]最先完成的,他们用不同量子化学计算方法对Cr(CO)6成键进行了能量分解分析,如表1所示,密度泛函理论(DFT)所得结果与实验值最为接近。

表1 不同理论方法计算的Cr(CO)6成键中的分解贡献能值(单位kJ/mol)
第一步:Cr从基态(d5s1)7S激发到()1A1g,将C—O键伸长到与金属配位键合后的键长值,从而得到所谓的“键准备”能 ΔEprep,从表 1可知,Cr d5s1→“激发”能很大,达970.7kJ/mol,而6个CO的C—O键伸长仅需25.1kJ/mol;第二步:将“激发”后的Cr原子插入6个CO形成的八面体笼中,计算配体和中心金属间的静电相互作用能,其中,(CO)6笼的形成产生-108.8kJ/mol的稳定化能,而Cr的插入导致-1138.0kJ/mol的稳定化能;第三步:由于第二步中形成的Cr(CO)6的电子分布违反Pauli原理,故需计算相同自旋电子之间的Pauli排斥作用,可以看出Pauli排斥作用中Cr(CO)6的电子排斥作用(1493.7kJ/mol)远大于(CO)6笼的形成中的电子排斥作用(460.2kJ/mol);第四步:轨道相互作用:即计算中心金属与配体对称性匹配轨道之间的相互作用,与前述几种作用强度相比,金属与CO的轨道相互作用并非最强,ΔEorb中不同对称性的轨道对成键能贡献的分解分析表明了 t2g轨道对能量的贡献为-853.5kJ/mol(即金属向 CO π反馈键的作用)远大于 σ轨道对成键能的贡献(-284.5kJ/mol)。
3.2 TMq(CO)6(TMq=H f2-,Ta-,W,Re+,Os2+,Ir3+)的能量分解分析
图4所示为配体之间以及配体与金属间对称性匹配的轨道之间的相互作用示意图,金属的价轨道分别为s,p,d轨道,金属的5个简并d轨道在六配位的八面体场中分裂为能量较高的eg轨道(dz2,dx2-y2)和能量较低的t2g轨道(dxy,dyz,dxz)。本文所考虑的过渡金属原子或离子都为d6电子组态,所以6个d电子恰好全部占据金属的t2g轨道,而eg及更高能量的轨道则全为空轨道。轨道相互作用主要可分为3种类型:σ型相互作用、π型相互作用及配体轨道自身的弛豫。即,σ型相互作用:对称性为eg,a1g,t1u的配体群轨道上CO的π电子占据轨道分别向金属中空的dz2,dx2-y2(对应eg对称性),s(对应a1g),p(对应t1u)轨道授予电子形成σ键;π型相互作用:金属中电子占据的dxz,dxy,dyz轨道(对称性为t2g)向对称性为t2g的配体群轨道反馈电子形成反馈π键,以及对称性为t1u的配体群轨道向空的金属p轨道授予电子形成π键,而后者相互作用常被遗漏;配体轨道之间的松弛:虽然作用较弱,也会产生一定的稳定化作用。

图4 TMq-(CO)6中轨道的相互作用示意图
表2为密度泛函理论对几个金属羰基配合物进行计算所得的不同相互作用对成键能的贡献值。可以看出,第一,随金属羰基配合物中心金属-第三过渡系金属从左至右的变化,其轨道相互作用能(ΔEorb)的变化和总的结合能(∑ΔE)变化大体相似,且数值接近。第二,体系的静电相互作用随金属所带电荷的变化而变化很小。当金属带更多的正电荷时(比如Ir3+),金属和CO配体的静电相互作用能并非想象的那样显著增加,因此,与人们的常规认识有所不同。我们认为这是由于静电相互作用根源于静电引力和斥力二者的折中的缘故:当金属所带正电荷增加时,其对配体CO的吸引增强,金属的价轨道和CO配体将同时向金属中心收缩,在引力急剧增加的同时,斥力也由于电子的相互靠近而急剧增加,从而两相互作用几乎抵消。第三,Pauli排斥作用能和静电相互作用能几乎抵消,所以总成键结合能主要是与轨道相互作用能对应。第四,轨道相互作用中不同轨道对成键能的贡献和金属所带电荷密切相关(这一点也是最重要的认识)。可以清楚地看出,除了t2g轨道,其他所有轨道对成键能的贡献都随金属所带正电荷的增加而增加。对于配体群轨道的t1g和t2u对成键能的贡献,随金属所带正电荷增加,金属对配体的吸引增强,配体相互间靠得更近,从而配体间的轨道弛豫增强,即成键增强; eg,a1g,t1u对成键能的贡献源于随金属所带正电荷的增加,配体向金属空轨道的授予电子能力增强;但对于t2g轨道,其能量贡献则随金属所带正电荷的增加而几乎线性减少,即,随着金属所带正电荷的增加,金属的电子占据轨道t2g(dxy,dyz,dxz)向配体t2g轨道反馈电子能力降低,因此M与CO形成的反馈π键也相应减弱,与前述的各对称性轨道(eg,a1g,t1u,t2u,t1g)对成键能的贡献趋势正好相反,在两种相反趋势的轨道作用贡献下,总的M—CO结合能呈U形分布。所以,当金属为中性或者带负电荷时,对成键能的贡献主要源于t2g(电子流向:M→CO),而当金属带正电荷时,则主要来自于eg(电子流向:M←CO),如Ir(CO)情形,甚至t1u,即配体与金属p轨道作用的贡献(-700.0kJ/mol)也要比t2g(-183.3kJ/mol)大很多。所以,并非所有的金属-羰基配合成键中均为金属向CO的π反馈的成键方式占主导。
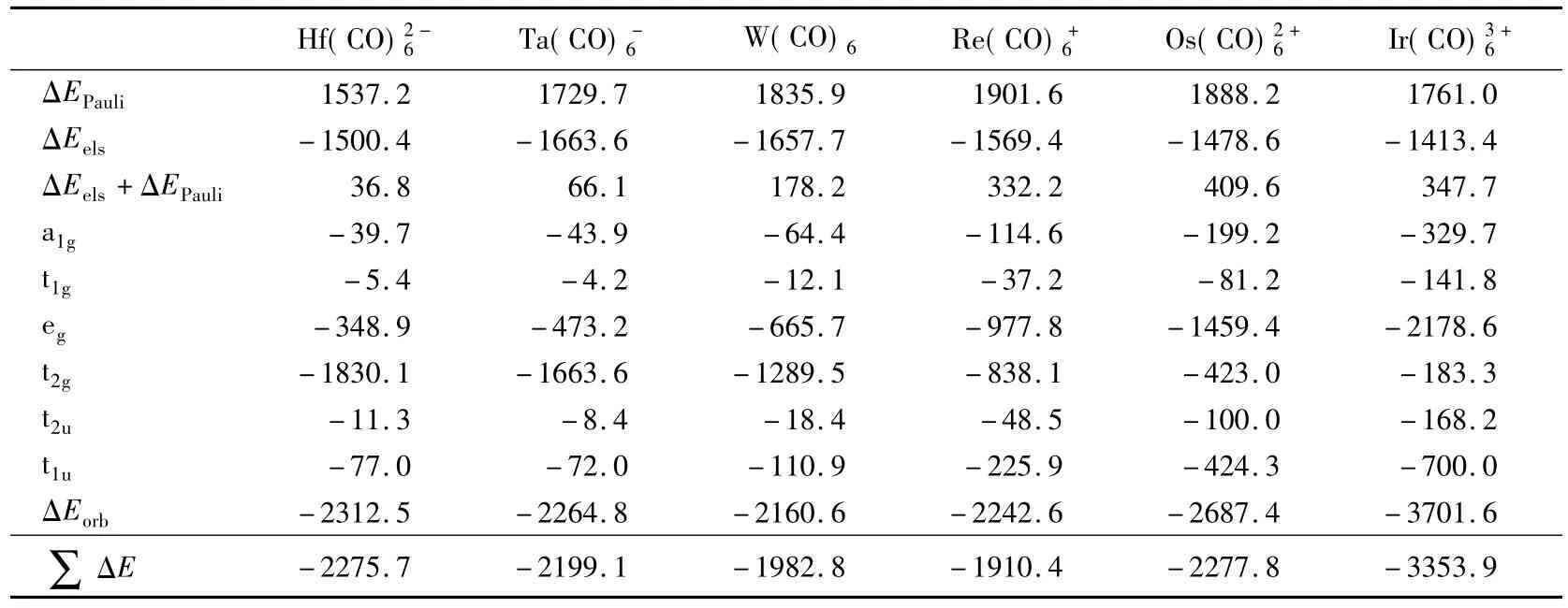
表2 DFT计算的TMq(CO)6成键作用中分解能量值[6](单位k J/mol)
4 结束语
本文论述了近年关于金属羰基配合物中的成键本质的理论研究进展,通过将成键能分解为物理意义明确的各部分贡献的详细分析而对金属羰基配合物的成键本质进行剖析。能量分解研究法可为化学键的概念和化学键的本质架起一座桥梁,不失为一种普遍的方法,从而可以有效运用于其他体系以探讨其化学成键本质。
[1] Santen R A,Neurock M.Molecular Heterogeneous Catalysis.Germany:WILEY-VCH,2005
[2] Szilagyi R,Frenking G.Organometallics,1997,16(22):4807
[3] Morokuma K.Acc Chem Res,1977,10(8):294
[4] Davidson E R,Kunze K L,Machado F B C,et al.JAcc Chem Res,1993,26(22):628
[5] Kunze K L,Davidson E R.JPhys Chem,1992,96(5):2129
[6] Diefenbach A,Bickelhaupt FM,Frenking G.JAm Chem Soc,2000,122(27):6449
国家基础科学人才培养基金(J0630429)
** 通讯联系人,E-mail:wsxia@xmu.edu.cn
