基于单核配位反应的定量演进方程

甘峰衷明华李莲云占达东

(1中山大学化学与化学工程学院 广东广州510275;2韩山师范学院化学系 广东潮州521041)

基于单核配位反应的定量演进方程

甘峰1，*衷明华2李莲云1占达东1

(1中山大学化学与化学工程学院 广东广州510275;2韩山师范学院化学系 广东潮州521041)

提出了定量演进方程的概念，用于描述单核配位反应过程中各组分的量的变化规律。定量演进方程将通过反应过程中的质量平衡以及反应物的体积比来建立。本文结果表明定量演进方程可很好地揭示单核配位反应过程各组分的浓度演进图景，有助于学生直观把握单核配位反应的进程。同时，定量演进方程也可用于稳定常数的计算。

在化学理论的建立过程中，数学方程式的使用是非常必要的，它使我们对于化学理论的描述更为准确和有效。常用的方程式有动力学方程和化学平衡方程。动力学方程在描述微观反应过程方面有其优势，而化学平衡方程在描述宏观反应过程方面更为常用［1－2］。除此之外，某些概念对于阐述化学反应过程也有很大的作用。例如分布分数在描述组分的宏观演进过程方面非常有用［2－4］。

另一方面，为同类型的化学反应建立描述化学反应进程的通式是提升化学理论知识系统水平的一个重要步骤。化学反应的通式可以用最简洁的方式综合化学反应的共同特征。Levie在建立酸碱滴定的通式方面做了非常有益的探索［5］，建立了任意复杂体系的酸碱滴定通式。受此启发，甘峰建立了基于EDTA的配位滴定通式，可准确描述复杂配位滴定体系中各组分的浓度变化过程［2，6］。

本文探讨建立单核配位反应的通式。由于单核配位反应是大学化学教育的一个重要内容，且在化学领域、生物领域和环境领域等方面有着广泛的应用。所以，单核配位反应通式的建立不但有利于学生把握该类反应的共同特征，同时也有利于学生运用该通式去解决实际问题。同时，我们提出定量演进方程的概念来表述单核配位反应的通式。原因在于这一概念能更好地揭示单核配位反应过程中各组分演进的直观图景。我们还将用经典的邻二氮菲与Fe(Ⅱ)的反应来演示定量演进方程在揭示反应进程方面的有效性。同时，我们也将通过反应体系的紫外可见光谱，借助定量演进方程来求出邻二氮菲与Fe(Ⅱ)反应的累积稳定常数。理论计算和实验结果都表明，定量演进方程在揭示单核配位反应体系的详细进程方面是有效的。

1 定量演进方程

反应物S与配位剂L之间的单核配位反应可用下式描述(为简便计，忽略电荷表达):

式中βi值是相应配合物的累积稳定常数，n是配位数。

要对上述反应进行定量描述，还需给定S与L之间进行定量反应的模型。常用的定量模型有摩尔比法和等摩尔连续变化法［2］。本文设计这样一种定量反应模型:将V0体积的S与Vt体积的L进行反应。设S和L的初始浓度分别为c(S)和c(L)，则质量平衡如下:

式中，方括号表示平衡浓度，α表示对应配合物的副反应系数，对于α(L)特别定义如下:

此处，h是L所能结合的最大氢离子数。

从方程(2)可得:

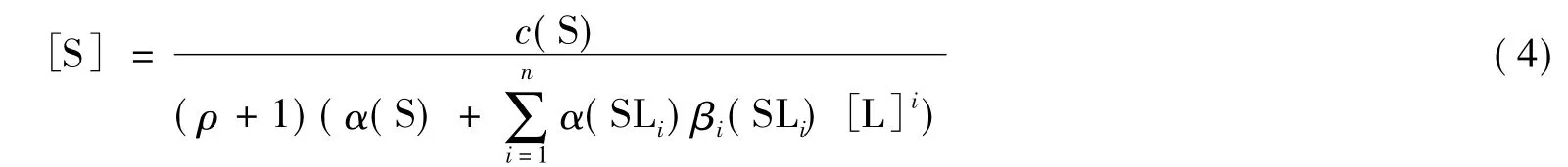
式中ρ=Vt/V0。

将方程(4)代入方程(3)，得:

称方程(4)和(5)为配位反应(1)的定量演进方程(Quantitative Evolving Equations)。从上面的推导过程可以看到，定量演进方程是基于具体的定量反应模型，通过质量平衡来建立的。不同的定量反应模型将建立不同的定量演进方程。这也可以解释我们为什么要用定量演进方程的概念来取代配位反应通式。我们也已经建立了基于摩尔比法和等摩尔连续变化法［2］的定量演进方程，限于篇幅，不将其列举在本文中。

方程(5)可以写成如下更为简洁的形式:

这里，

如果溶液中有m个物质S1，S2，…，Sm同时与L发生如下的单核配位反应:

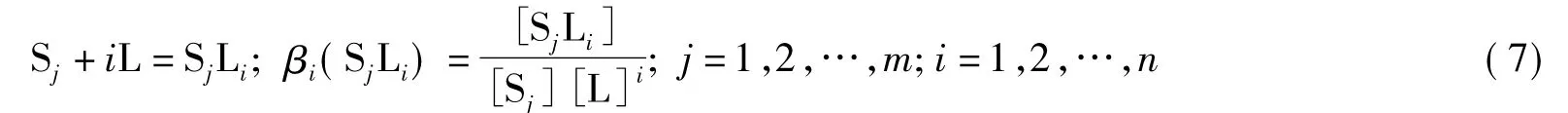
通过类似的推导，可得如下的定量演进方程(定量反应模型同上):

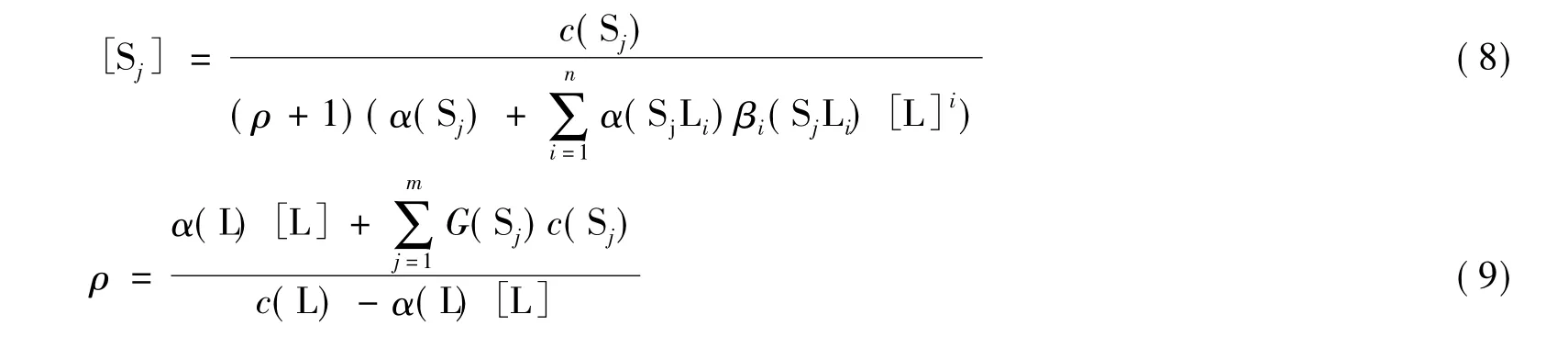
这里:

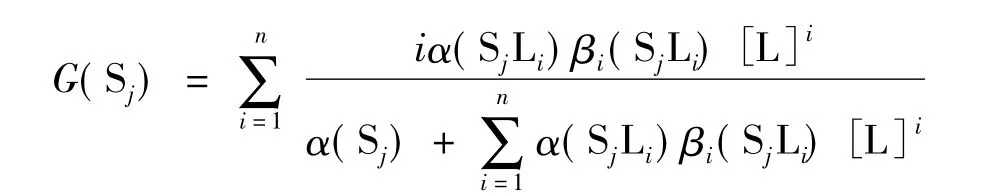
作为一个简单的推论，当所有的单核配位反应都是1:1型的配位反应时，方程(8)和(9)可简化为我们以前建立的配位滴定通式［2，6］。这也表明，定量演进方程具有更广泛的适用性。

2 实例分析

2.1 理论计算结果与实验结果的对比

经典的邻二氮菲与Fe(Ⅱ)的反应如下:

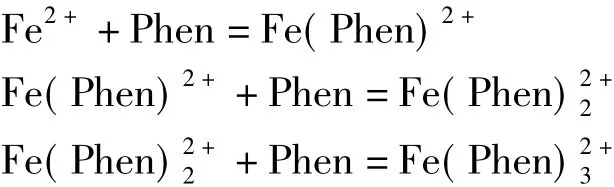
该反应的各累积稳定常数分别为lgβ1=5.9，lgβ2=11.1和lgβ3=21.3［7］。该反应通常在pH=5.8的乙酸和乙酸钠缓冲溶液中进行。在此酸度下，α(L)等于1.14。为简便计，我们设其他的副反应系数为1(如果有相关的参数的话，这些副反应系数都是可以计算的)。图1中的实线为计算出的各配合物的浓度变化曲线。有两个现象值得关注:其一是ρ大于3后，除Fe(Phen)外其他组分的浓度几乎为0，且在ρ等于3的位置Fe(Phen)的浓度出现一个拐点;其二是Fe(Phen)的浓度在整个反应过程中几乎为0。现象一很好地解释了为什么该反应可以成为采用分光光度法对Fe(Ⅱ)进行定量分析的有效方法;当ρ大于3时，单一配合物的存在使我们获得了确定的定量关系。现象二与Lee［8］等人的Fe(Phen)不稳定的结论是一致的。

此外，如果图1所示的计算结果揭示了反应的真实进程的话，那就应该能从实验中观察到在ρ=3时会出现一个明显的转折点。图2所示为510nm处吸光度与ρ的关系图。从中的确可以观察到在ρ=3时有一个明显的转折点，表明实验结果与理论计算结果是一致的。要说明的是，并非所有的反应体系都能观察到类似的现象。如果要观察到这个现象，一个基本的要求是在转折点处［SLn］的质量百分数不低于99.9%，由此可以得出一个判据lgβn－lgβ(n－1)≥6－lg［L］。

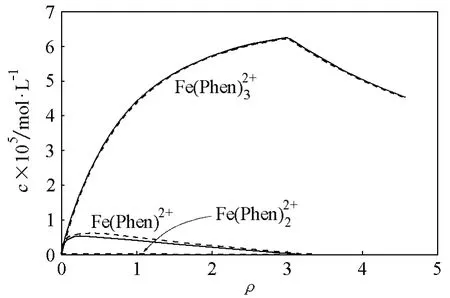
图1 邻二氮菲与Fe(II)反应的浓度曲线

图2 邻二氮菲与Fe(Ⅱ)的反应体系在510nm处的吸光度与体积比的关系图

2.2 累积稳定常数的测定

稳定常数是描述化学反应平衡的一个非常重要的量，也是大学化学教学的一个重要内容。在此，我们将使用定量演进方程并通过优化的方式从反应体系的紫外可见光谱中计算上述反应的累积稳定常数。

我们将实验过程中的紫外可见光谱表达为矩阵A。由于反应体系的浓度很小，故吸光度满足比尔定律。根据吸光度的加和性［2］，得:

这里，C是具有吸光度的组分的浓度矩阵，它可以从方程(4)和(5)求得;B是具有吸光度的组分的吸光系数矩阵;下标p表示具有吸光度的组分的数目;m是实验点的数目，本实验中使用了14个实验点，对应的体积比如图2所示;w是波长采样点数，本实验中的波长范围是400～600nm。

借助方程(10)，我们建立如下的估计稳定常数的优化模型:

这里，^Akl是矩阵^Am×w=Cm×p(Cm×p)+Am×w的矩阵元，上标+表示矩阵的广义逆;β是累积稳定常数构成的向量，当β为真实值的时候，E(β)将达到最小值。

我们采用序贯数论优化方法［9］来求解上述的优化问题，收敛判据为(Ei+1－Ei)/Ei≤0.0001，i为循环次数。在每一个循环中采用1220个好格子点(good lattice point)［9］。在每一个循环中，浓度矩阵C都根据当前的稳定常数预测值采用方程(4)和(5)进行计算。我们计算所得的稳定常数为lgβ1=6.5，lgβ2=11.5和lgβ3=23.0，对应的目标函数值(参见(11)式)为0.0159。如果将文献中的累积稳定常数值代入到(11)式，则目标函数值为0.0235。显然，我们的方法的拟合残差更小。在此要说明的是，在计算中仅考虑Fe(Phen)2+，Fe(Phen)， Fe(Phen)以及邻二氮菲的吸光度。原因在于，这些组分在反应过程中的浓度逐步增加。Fe(Ⅱ)的浓度非常小且在反应过程中浓度逐步减小，故其对总体吸光度的影响很小。

图1中的虚线为本文方法求得的累积稳定常数计算的浓度曲线，结果与文献数据的计算结果相吻合。文献数据最早可以追溯到Lee等人的工作［8，10］，他们是采用两种方法才获得这3个累积稳定常数值的;借助定量演进方程，我们从一组实验中就获得了这3个稳定常数值。由此也可以看到定量演进方程的实用性。

3 结论

定量演进方程可对单核配位反应的进程给出一个显式的描述，有利于揭示反应体系中各组分的详细演进图景，使我们能更好地把握反应的进程。从定量演进方程的建立过程可以看到，借助于反应过程的质量平衡以及反应物的体积比，可以很容易地建立对应的定量反应模型的定量演进方程。

［1］ McCleverty JA，Meyer T J.Comprehensive Coordination Chemistry.New York:Elsevier Ltd，2004

［2］ 甘峰.分析化学基础教程.北京:化学工业出版社，2007

［3］ Kealey D，Haines P J.Analytical Chemistry.London:Oxford Taylor＆Francis Routledge，2002

［4］ Skoog D A，West D M，Holler F J，et al.Fundamentals of Analytical Chemistry.London:Thomson Brooks/Cole，2004

［5］ de Levie R.Anal Chem，1996，68:585

［6］ 甘峰.大学化学，2007，22(5):54

［7］ 常文保，李克安.简明分析化学手册.北京:北京大学出版社，1981

［8］ Lee T S，Kolthoff IM，Leussing D L.JAm Chem Soc，1948，70:3596

［9］ Fang K T，Wang Y.Number－theoretic Methods in Statistic.London:Chapman＆Hall，1994

［10］ Kolthoff IM，Leussing D L，Lee T S.JAm Chem Soc，1950，72:2173