理想稀溶液的分子模型与Henry系数

刘国杰 黑恩成

(华东理工大学化学系 上海200237)

自学之友

理想稀溶液的分子模型与Henry系数

刘国杰 黑恩成

(华东理工大学化学系 上海200237)

提出了一个理想稀溶液的分子模型，并利用Boltzmann分布定律和Laplace方程导出一个简单的Henry系数表示式，它与溶质分子周围溶剂的内压力或溶剂压密切相关。利用Hildebrand内压力方程，并以纯溶剂的摩尔体积代入，关联了11种气体在正十六烷中的Henry系数随温度变化的实验数据。

在无限稀释的溶液中，溶剂服从Raoult定律，溶质服从Henry定律。从这个事实出发，在研究液体混合物和溶液时，建立了两个理想模型——理想液体混合物和理想稀溶液模型。前者是在任何温度和压力下所有组分都遵守Raoult定律的液体混合物;后者是溶剂遵守Raoult定律、溶质遵守Henry定律的稀溶液。这两个模型对进一步研究多组分系统的热力学和溶液理论起着至关重要的作用。本文将专注于理想稀溶液的溶质，从分子模型入手，研究Henry定律，旨在给Henry系数以定量的描述。

1 理想稀溶液的分子模型

设有一无限稀释的溶液，因溶质分子②与溶剂分子①间的相互作用，每个溶质分子都被溶剂分子所包围，分子②犹如囚禁在分子①构成的“笼子”里(图1(a))。

图1 无限稀释溶液的微观模型示意

假如溶质分子与溶剂分子间不再相互作用，那么溶质分子②就完全处在自由状态(图1(b))。由于溶质分子②不与溶剂分子①作用，而且溶质分子间的作用以及溶质的体积相比于溶液也因无限稀释而可忽略不计，故此时溶质分子②如同理想气体分子。倘若溶液的体积为V，温度为T，溶剂和溶质分子数分别为N1和N2，则由理想气体状态方程可得溶液中溶质产生的压力为:

式中k为Boltzmann常量。

于是，按照 Boltzmann能量分布定律，不难得到当溶质与溶剂分子间存在相互作用(图1(a))时，处于完全自由状态的溶质分子数N2'应为:

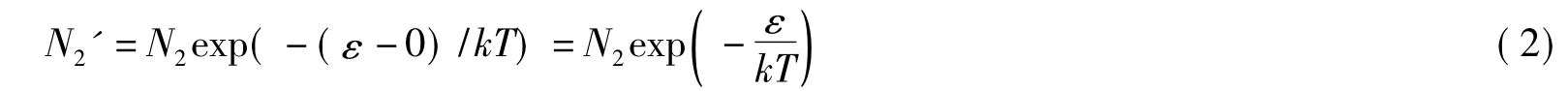
式中ε为克服溶剂分子的包围而变成完全自由的溶质分子所需的能量。由式(2)知图1(a)和图1(b)的自由溶质分子数之比等于它们的Boltzmann因子之比。因此，无限稀释溶液中溶质产生的压力应为:

因溶液中溶剂和溶质的分子总数N=N1+N2，溶质的摩尔分数x2=N2/N，在无限稀释溶液中，一个溶剂分子所占的体积v1=V1/N1≈V/N，将这些条件代入式(3)，得:

式中KH即为Henry系数，由此可见，只要解决ε的计算问题，就可获得Henry系数。

2 溶剂压与Henry系数

上面已述，ε是克服溶剂分子包围而变成完全自由的溶质分子所需的能量。不难想象，当一个溶质分子获得ε能量而跃出溶剂分子包围的“笼子”时，就像在溶剂中制造了一个空腔。－ε则相当于将一个完全自由的溶质分子引入空腔所需做的可逆功，即Gibbs自由能增量δG。因此，在恒温、恒压和各组分物质的量不变的条件下，有:

式中As为空腔的表面积;δV为一个空腔的体积，其值等于一个溶质分子所占的溶液体积v2;γ为空腔的表面张力。故式(4)中的

这个压力来自于邻近溶质分子的溶剂，在本文中称其为溶剂压。

Rosseinsky［1］已由热力学关系G=H－TS≈U－TS给出，在恒温、恒压和恒物质的量的条件下，有:

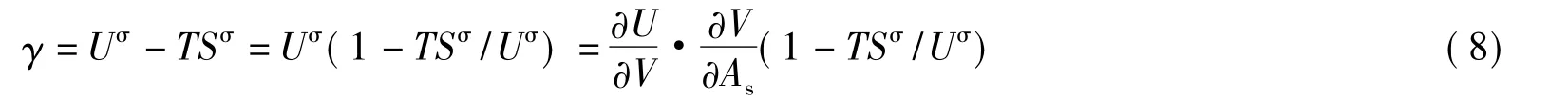
式中Uσ和Sσ分别为空腔的比表面热力学能和比表面熵，∂U/∂V为空腔周围溶剂的内压力pi。将式(8)代入式(7)，可得:

式中α=1/(1－TSσ/Uσ)=Uσ/Aσ，其中Aσ为比表面Helmhotz自由能，由于Uσ=Aσ+TSσ，而Sσ=－(∂γ/∂T)p＞0，故α＞1，且在一般温度范围内是温度的弱函数。现将式(9)代入式(6)，则得:

因此，由式(10)和式(4)便得Henry系数的表示式为:

这里，可有以下两种情况:

一是溶质分子与其周围的溶剂分子作用较弱，即它们之间的吸引力较弱，则空腔或溶质分子周围的溶剂分子不是排列得很紧密，就像图2(a)所示。此时溶剂分子间的作用是以吸引力占优势，内压力和溶剂压都是正值。于是，按照热力学关系(∂μ/∂p)T=Vm，溶质分子的化学势因受溶剂压作用而增大，使溶质分子逸出“笼子”的能力增加，故Henry系数随之增大，且因此时式(11)中Boltzmann因子大于1，KH＞RT/。

二是溶质分子与其周围的溶剂分子作用较强，即它们间的吸引力较强，则空腔或溶质分子周围的溶剂分子排列紧密，就像图2(b)所示。此时，溶剂分子间的作用变成排斥力占优势，内压力和溶剂压都呈负值，溶质分子的化学势便因承受负的溶剂压而减小，它逸出“笼子”的能力和Henry系数因此而减小，且因此时式(11)中的Boltzmann因子小于1，KH＜RT/V1。

图2 溶质分子与其周围溶剂分子的作用状况

3 模型的检验

已知分子间的作用势能u(r)与分子间距r的关系可由下式表示:

式中等号右边两项分别为吸引力和排斥力对作用势能的贡献。Hildebrand［2］由式(12)出发，建立了如下液体内压力的公式:

式中M=m/3，N=n/3，α是引力常数(α∝A)，Vm为液体的摩尔体积，Vm，0为pi=0时液体的摩尔体积。现假定这个公式也适用于空腔周围的溶剂。则将式(11)取对数，并将式(13)代入其中，可得:

图3是溶质H2、N2、CO、CO2、SO2、HCl、H2S、NH3、C2H6、C3H8和n－C4H10在溶剂正十六烷(n－C16H34)中Henry系数随温度的变化关系。它们来自文献［3－5］中的上述11种气体在正十六烷中的溶解度数据。图3中数据点为实验值，曲线为式(14)关联值。可见，不管Henry系数是随温度升高而增大还是减小，式(14)都能够满意地关联。表1是关联得到的参数值和ln KH的拟合标准偏差SD，其定义为

式中N为参与拟合的实验数据点的数目。

图3 若干气体在正十六烷n-C16H34中Henry系数与温度的关系

表1 式(14)参数值与拟合的标准偏差

4 讨论

在图3中有一条虚线，这就是KH=RT/Vm，1线。在300～475K温度范围内，H2、N2和CO的Henry系数都在这条虚线的上面，表示它们的KH＞RT/Vm，1，这说明在无限稀释溶液中，这3种溶质分子与溶剂n－C16H34的作用较弱，它们承受着正的溶剂压，具有较大的逸出“笼子”的能力。C2H6、H2S、SO2、C3H8和n－C4H10的Henry系数则在虚线的下面，表明它们的分子与溶剂有较强的作用，特别是n－C4H10和C3H8，这是因为它们与溶剂都是烃类分子，且随着碳原子数增多，作用迅速增强。故它们都承受着负的溶剂压，较难从“笼子”中逸出，即KH＜RT/Vm，1。其余3种溶质则介于其间，它们的Henry系数在温度较低时在虚线的下面，温度较高时在虚线的上面，表明它们的分子与溶剂的作用随温度升高而变弱。

应该指出，根据上述模型，表1中参数Vm，0应有相同的数值，因为Vm，0为溶剂在pi=0时的摩尔体积，其值仅与溶剂本性有关。但是表1拟合结果与溶质有很大关系，尤其是溶质为C3H8和n－C4H10时，Vm，0值远大于其他溶液，这要归因于本文在用式(13)计算溶质分子周围溶剂的内压力时，采用了体相溶剂的摩尔体积Vm，1，这是无奈之举，因为无法知道溶质分子周围溶剂的密度。其实，溶质分子周围溶剂的密度与体相溶剂的密度有显著的区别，溶质分子与溶剂的作用愈强，两者的差别愈大。在统计力学中，两者的比值相当于溶质分子的第一配位圈的径向分布函数值。所谓径向分布函数，是距离指定分子为r处，分子的局部数密度与平均数密度之比［6］，即g(r)=ρ(r)/ρ。对于无限稀释溶液，它可由图4表示。

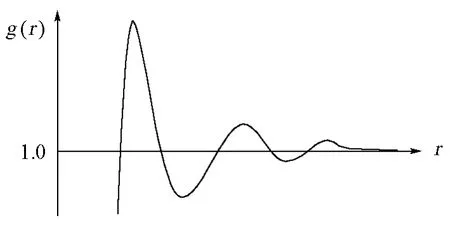
图4 液体的径向分布函数随分子间距的变化

如果指定分子为一个溶质分子，则其周围的溶剂分子即代表第一配位圈，它的径向分布函数值相当于图4中曲线的第一个峰值，g(r)明显地大于1.0。可见，该处溶剂的局部数密度显著地高于平均数密度(即体相数密度)。由于径向分布函数只有通过X射线或中子衍射等实验才能测得，故本文不得不用溶剂的体相摩尔体积来取代溶质分子周围溶剂的摩尔体积，这便使表1中参数Vm，0的值不再相同，而是随溶质分子与其周围溶剂分子作用的增强而变大。

［1］ Rosseinsky D R.JPhys Chem，1977，81:1578

［2］ Hildebrand JH.Phys Rev，1929，34:984

［3］ Young C L.Solubility Data Series.Vol5/6.Oxford:Pergamen Press，1981

［4］ Tremper K K，Prausnitz JM.JChem Eng Data，1976，21:295

［5］ Prausnitz JM，Chappslow L L.AIChE J，1974，20:1097

［6］ 胡英，刘国杰，徐英年，等.应用统计力学－流体物性的研究基础.北京:化学工业出版社，1990