一种求解屏蔽电缆场线耦合问题的混合方法

张 刚 王立欣 刘 超

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001)

1 引言

随着空间电磁环境日趋复杂，测试系统中用于传输微弱信号的屏蔽电缆很容易受到外部电磁骚扰的影响，成为电磁能量的吸收器，从而影响数据测量精度，严重时甚至导致系统不稳定。

求解屏蔽电缆场线耦合问题的关键在于求解在外界电磁场干扰下，电缆屏蔽层和芯线上电压和电流的响应。传输线理论能够对电缆结构进行等效处理[1-2]，因而得到广泛应用。但随着电缆周围环境复杂程度的提高，传输线理论并不能对屏蔽电缆所在电磁环境进行准确分析。

而随着计算机计算速度和存储容量的不断增长，近年来，能够进行电磁场三维全波分析的时域有限差分方法（FDTD）得到快速发展，提出了针对细长结构的Holland细线算法[3]，从而被应用于求解屏蔽电缆场线耦合问题。但这种全波分析方法在求解电缆内部结构电压、电流响应时，仍有困难，一般只用来求解屏蔽层的响应[4-6]。

本文结合以上两种方法的优点，研究了一种针对屏蔽电缆场线耦合问题的混合方法。利用电磁场FDTD方法对屏蔽电缆外部空间的电磁环境进行准确建模，描述屏蔽电缆铺设于有耗地面时，屏蔽层感应电流的分布。而对于受外界环境影响较小的电缆内部，则应用传输线理论，将电缆内部等效为一组带分布源的传输线方程，计算芯线上的感应电压和感应电流。该方法结合了三维全波分析对空间电磁环境模拟的准确性和传输线理论对电缆内部细微结构处理的有效性，解决了单纯应用两种方法的不足。

2 数值计算模型及方法

电缆结构和空间电磁场入射方位如图1所示，长度为l的屏蔽电缆距离有耗地面高度h平行放置，σ 和εr分别为土壤电导率和相对介电常数。屏蔽层两端接地电阻分别为Za、Zb，芯线和屏蔽层端接地电阻为Z1、Z2。k为平面电磁干扰入射方向，φ 为入射方位角，θ 为入射仰角。

图1 电缆和空间入射电磁波方位图Fig.1 Geometry of the cable and incident electromagnetic wave

数值模型分为内系统、外系统两部分，电缆屏蔽层、外部电磁场以及大地构成外系统，屏蔽层和芯线构成内系统。求解算法如图2所示。

3 屏蔽层响应的计算

外系统的建模是利用电磁场的 FDTD方法进行，主要包括有耗地面、空间入射电磁波、屏蔽电缆。将计算空间划分若干Yee网格，并对Maxwell方程进行离散迭代。由Maxwell方程

图2 混合求解算法Fig.2 Hybrid method

其中，有耗地面只要将仿真区域内相应网格的电导率σ 和相对介电常数εr设定为对应土壤的参数值，就可以模拟不同土壤结构对屏蔽层响应的影响。计算时，将计算区域划分为总场区和散射场区，在总场边界加入平面波模拟空间电磁场干扰，干扰波形可以根据不同问题进行设定。

采用传统FDTD方法分析电缆问题时，由于其线径小、长度长，导致划分网格数过多，计算存在困难。应用Richard Holland等提出的细线算法[3]，可以将细导线上的感应电流作为电流源参与Maxwell方程的迭代计算，直接得到电缆屏蔽层电流分布。由于计算空间内包括有耗土壤，吸收边界采用有耗介质的各向异性介质完全匹配层（UPML)[7]，可以实现对有耗介质中电磁波的无反射吸收。利用以上方法可以实现在不同土壤结构和电缆结构下对屏蔽层响应的计算。

算例1：电缆结构如图1所示，l=6m，h=0.8m，电缆屏蔽层双端直接接地，即Za=Zb=0Ω。水平极化平面波入射仰角θ =0°，入射方位角φ =0°，入射波形采用标准美国Bell实验室电磁脉冲波形：

脉冲幅值 Eo=5.25×104V/m。计算分别取土壤电导率σ 为0.001S/m、0.01S/m和0.1S/m，相对介电常数εr=10时，对屏蔽层感应电流的影响。计算结果如图3所示。

从计算结果可以看出，随着土壤电导率的增大，感应电流幅值减小。这是因为随着电导率的增大，地面对入射波的反射增强，反射波的水平电场分量对空间入射波的水平电场分量抵消增大，使得耦合到电缆上的能量减少。当σ =0.001S/m时，由于屏蔽层两端直接接地，未进行阻抗匹配，加之土壤导电性变差，使得屏蔽层上感应电流发生振荡。

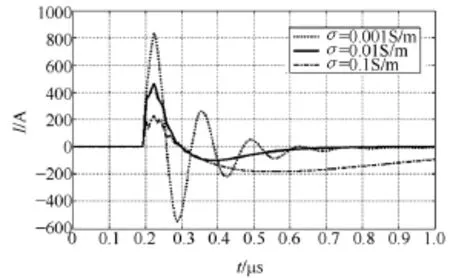
图3 不同土壤电导率下的屏蔽层中端电流Fig.3 Sheath current in the middle point with different earth conductivity

算例 2：为了验证本算法对外系统求解的正确性，参照文献[8]实际测量参数的设置，取l=40m，h=3.5m。土壤电导率σ =0.01S/m，相对介电常数εr=10，入射波设置同算例1。分别计算电缆屏蔽层在双端接地、双端悬空、单端接地情况下屏蔽层中部电流波形。计算结果如图4a所示，图4b是文献[8]的实际测量结果。

图4 不同接地方式下的屏蔽层中端电流Fig.4 Sheath current in the middle point with different grounding methods

对于外系统，电磁波传输介质是空气，传输速度为光速 c。当屏蔽层双端开路时，感应电流在电缆两端均发生反射，并由于辐射和欧姆损耗而逐渐衰减。所以，波形为衰减振荡波，振荡周期由电缆长度l和电磁波沿电缆传播速度c决定：T=2l/c，则振荡周期理论值为0.267µs。当单端接地时，电流只在开路端反射，所以在电缆上来回两次才形成一次反射倒相，振荡频率是双端开路情况下的 1/2，振荡周期理论值为0.533µs。计算结果和测量结果也证实了这一点，双端开路和单端接地时振荡周期的实际计算值分别为0.286µs和0.556µs。实际数值偏大的原因是电缆近地铺设，屏蔽层对地电容减慢了波的传播速度。当双端接阻抗与屏蔽层特征阻抗匹配时，电流在电缆上传播不会发生反射，只是按指数衰减，这也与测量和计算结果一致。

通过以上分析，可以看出，对外系统应用电磁场FDTD方法能够实现对不同土壤结构和电缆结构屏蔽层响应的准确仿真。

4 芯线响应的计算

外系统计算得到的屏蔽层分布电流可以通过转移导纳和转移阻抗等效为内系统的分布电流源和分布电压源，进而利用传输线理论计算芯线的响应。转移阻抗是衡量电缆屏蔽性能的有效标准，转移阻抗越大，电缆屏蔽性能越差[9]。一般地，编织型屏蔽电缆的转移阻抗计算公式可以表示为

式中 ZT——散射阻抗；

Mh——小孔电感；

Mb——编织电感。

对于管状屏蔽电缆，可以忽略后两项的影响。另外，由于管状屏蔽具有良好的完整性，转移导纳亦可忽略不计。

将内系统等效为如图5所示的传输线模型，可用如下传输线方程描述

式中 uF，iF——单位长度等效电压、电流激励源；u(z,t)，i(z,t)——芯线单位长度上瞬态电压、电流；

Ri，Li——内系统单位长度的电阻、电感；

Gi，Ci——内系统单位长度的电导和电容。

图5 内系统传输线等效电路Fig.5 Equivalent circuit of the transmission-line in the inner system

由于外系统采用电磁场FDTD方法求解，为了便于内外系统间计算程序的连接，同时获得时域解，对于内系统传输线方程亦采用FDTD方法求解。即分别以中心差商代替以前向差商代替对式（3）和式（4）进行空间和时间上的离散。离散后的方程为

整理可得

其中，对于单位长度等效分布电流源iF而言，实际计算中影响较小，可以忽略不计，只需要计算分布电压源uF。根据外系统计算得到的屏蔽层分布电流io(z,t)以及屏蔽电缆的转移阻抗ZT可以计算uF。

对式（9）进行时间上的离散可得

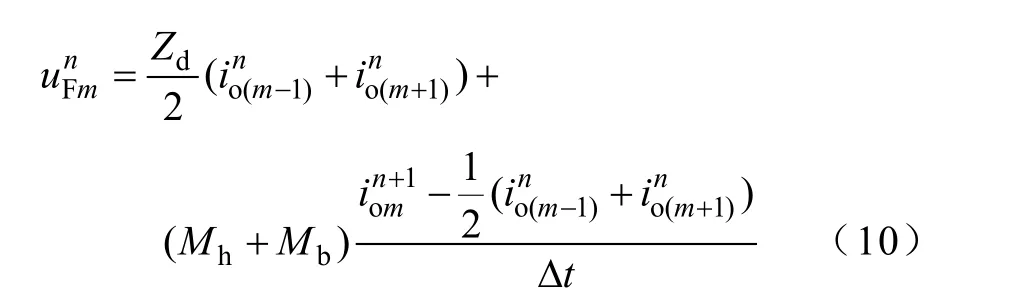
以上就是计算芯线响应的迭代公式，可以看出，只要得到m点两侧m+1和m-1点的上一时刻的分布电压和电流值以及屏蔽层的分布电流值，就可以得到m点当前时刻的值。进行迭代时只要给出初始值和首末端边界条件，就可以利用外系统计算的屏蔽层不同位置和不同时刻的电流值io(z,t)，得到外部电磁场作用下的芯线上的时域响应。

以芯线两端分别接电阻R1，R2为例，由图5可知，首末端电流电压值 i1、u1、iM、uM满足如下边界条件

首端

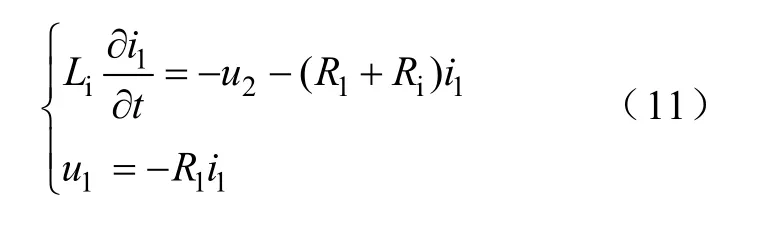
末端

算例 3：为了验证本算法对芯线响应计算的准确性，参照文献[10]给出的数据，应用混合算法分别求解电缆的内系统和外系统，得到芯线的响应。

电缆设置：l=6m，h=0.735m，芯线材料为铜，半径r=0.785mm，电缆内部填充介质相对介电常数有εr=1.45。屏蔽层材料为铝，外半径a =3.825mm，内半径 b=3.625mm，屏蔽层两端接地电阻Za=Zb=1Ω，芯线和屏蔽层端接电阻Z1=Z2=75Ω。电缆参数计算可参照文献[9]。垂直极化入射平面波入射仰角θ =1°，入射方位角φ =0°。入射波形为双指数脉冲其截止频率为 35MHz，对应波长为 8.5m，一般为保证计算稳定性取空间步长∆Zmax=λmax/10，λmax为截止频率对应波长[11]。为了提高计算精度，取∆Z=0.2m。

图6所示的三条曲线分别为采用本算法得到的屏蔽电缆芯线末端电压波形、文献[10]中的实际测量波形、文献[10]应用等效传输线方程的计算波形。使用传输线方程对外系统进行计算时，由于外系统的屏蔽层和大地之间的单位长度参数受电缆周围环境影响较大，对于电缆参数的计算只能近似处理，不能准确分析电缆周围环境对计算结果的影响。所以文献[10]中的计算结果和测量结果存在较大差异。而从图6中可以看出，混合算法相对于单纯应用传输线理论的求解方法更接近实测结果，这是因为混合算法在求解外系统时，采用了电磁场 FDTD方法，这种三维全波分析方法能够更准确地模拟电缆所处的电磁环境，使得对屏蔽层电流分布情况的计算更准确，最终求得芯线上的电压响应也就更接近实际测量结果。

图6 芯线末端感应电压波形Fig.6 Waveforms of the core wire induced voltage at the terminal

5 结论

电磁场FDTD法和传输线理论相结合的混合方法能够很好地求解屏蔽电缆场线耦合问题。利用此方法计算了不同土壤电导率下屏蔽层电流波形，结果表明，感应电流随着土壤电导率的增大而减小。应用混合算法计算得到的屏蔽层电流波形和芯线电压波形与相关文献的实测波形具有很好的一致性，证明该场路混合求解方法是准确、有效的。

[1]Paul C R. Analysis of multiconductor transmission lines. New York： John willy & Sons, 1994.

[2]Paul C R. A brief history of work in transmission lines for EMC applications[J]. IEEE Trans. on EMC,2007, 49(2)： 237-252.

[3]Holland R, Simpson L. Finite-difference analysis of EMP coupling to thin struts and wires[J]. IEEE Trans.on EMC, 1981, 23(2)： 88-97.

[4]Berenger J P. A multiwire formalism for the FDTD method[J]. IEEE Trans. on EMC, 2000, 42(3)：257-264.

[5]Chen B, Chen H L, Gao C, et al. Study on the HEMP induced current in the two-wire line with the metal shielded bushing[M]. The Third Asia-Pacific Conference on Environmental Electromagnetics Proceedings, Hangzhou, 2003, 255-259.

[6]Feliziani M, Maradei F. Full-wave analysis of shielded cable configurations by the FDTD method[J].IEEE Trans. On Magn., 2002, 38(2)： 761-764.

[7]Gedney S D. An anisotropic perfectly matched layer absorbing media for the truncation of FDTD lattices[J]. IEEE Trans. on Antennas and Propagation,1996, 44 (12)： 1630 -1639.

[8]周启明, 罗学金. 架空线和地面电缆的 HEMP耦合模拟试验[C]. 全国电磁兼容专题学术研讨会论文集, 2000： 60-67.

[9]Vance E F. Coupling to shielded cables[M]. New York： John Wiley & Sons Press, 1978.

[10]Michel A, Mircea I, Lin C C. Transient electromagnetic field coupling to long shielded cables[J].IEEE Trans. on Electromagnetic Compatibility, 1980,22(4)： 276-282.

[11]葛德彪, 阎玉波. 电磁波时域有限差分方法[M]. 西安：西安电子科技大学出版社, 2002.