带双井势函数的一维p-Laplace方程解对应层的位置
2010-06-27周斌,何丹
周 斌,何 丹
(湖南工学院 基础课部, 湖南 衡阳, 421002)
带双井势函数的一维p-Laplace方程解对应层的位置
周 斌,何 丹
(湖南工学院 基础课部, 湖南 衡阳, 421002)
研究了一类带双井势函数的一维p-Laplace方程解,主要讨论了方程解对应层的位置情况. 解的零点与交换层是一一对应的,得出方程解对应的层出现在()h x的局部极值点附近. 在()h x的局部极小值点附近只可能出现一个交换层,而多层出现在()h x的局部极大值点附近.
p-Laplace;双井势函数;n-模解;层
Allen-Cahn 方程是一个著名的两相过渡模型,对于一维的Allen-Cahn 方程多层解的相关性态, Kimie Nakashima在文献[1-2]中已经给出了详尽的讨论.
本文是Allen-Cahn方程的一个推广,将Allen-Cahn方程中的Laplace算子换成p-Laplace算子后,着重讨论了下列问题解的交换层位置的分布情况,即:

1 定理与命题


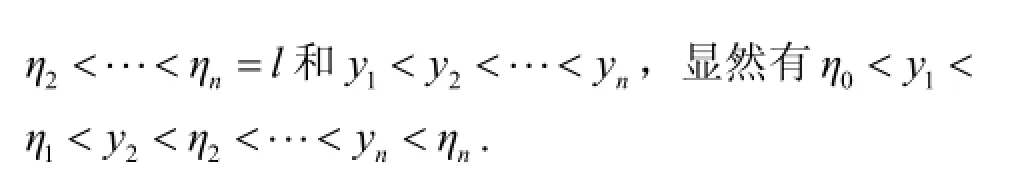
2 引理及定理的证明



这与式(11)矛盾. 故命题2得证.
命题3的证明 考虑α( y)≥0的情形[5-8],假设(y)在y=0附近有一个零点,将y=0附近最右端的零点记作yk,将a∗看作0,重复命题2的证明过程,即得证. 当α( y)≤0时,同理可证.
[1] Nakashima K. Stable transition layers in a balanced bistable equation[J]. Differential and Integral Equations, 2000, 13: 1025-1038.
[2] Nakashima K. Multi-layered stationary solutions for a spatially inhomogeneors Allen-Cahn equation[J]. J-Differential Equations, 2003, 191: 234-276.
[3] 周斌, 何丹. 带双井势函数的一维p-Laplace方程解的零点分布[J]. 邵阳学院学报: 自然科学版, 2010, 7(3):6-8.
[4] 周斌, 何丹. 两相模型的导数估计[J]. 经济数学, 2010, 27(3): 24-27.
[5] Wong Fu-Hsiang. Uniqueness of Positive Solutions for Sturm-Liouville Boundary Value Problems[J]. Proceedings of The American Mathematical Society, 1998, 126:365-374.
[6] Lucio Damascelli. Comparison theorems for some quasilinear degenerate elliptic operators and applications to symmetry and monotonicity results[J]. Nonlinerar Analysis, 1998, 15: 493-516.
[7] Gui C, Schatzman M. Symmetric quadruple phase transition[J]. Indiana University Mathematical Journal, 2008, 57: 781-836.
[8] Rabinowitz P H. Some global resulets for nonlinear eigenvalue problems [J]. J Funct Anal, 1971, 7: 487-513.
The locatin of the layers of the solution to a class of one-dimensional p-Laplace equation with double well potential
ZHOU Bin, HE Dan
(Basic Department, Hunan Institute of Technology, Hengyang 421002, China)
The problem of the location of the layers of the solution to a class of one-dimensional p-Laplace equation with double well potential was put forward. There is an one-one correspondence between the zeros and the layers of the solutions. The layers only appear near the local extreme points of ()h x. At most a single layer can appear near each local minimum point of ()h x, the multi-layers can appear near the local maximum point of ()h x.
p-Laplace; double well potential equation; n-mode solution; layers; distribution of the zeros
O 175.29
:A
1672-6146(2010)04-0011-03
10.3969/j.issn.1672-6146.2010.04.004
2010-08-04
湖南省教育厅科研课题(10C0586)
周斌(1979-), 男, 硕士, 研究方向为应用数学.
