计算流体力学三维非结构网格可视化的高效算法研究

2010-06-26马志强

黑龙江水利科技 2010年1期

马志强，多佳，李曼

(1.大连理工大学土木水利学院，辽宁大连 116024;2.黑龙江科技学院数力系，哈尔滨 150027;3.黑龙江省水利水电勘测设计研究院，哈尔滨 150080)

1 引言

随着有限元(FEM)和有限体积法(FVM)等离散方法的发展和计算机自身运算能力的提高，三维流体力学数值模拟越来越多的得到应用，由于对复杂地形的适应性较强，因此大部分三维流体力学数值模拟都采用非结构网格。针对这种数据结构，如何把计算结果高效快速的动态显示出来是计算流体力学科学可视化的面临的一个问题[1]。

由于在一般的三维可视化过程中需要显示的只是所选择的计算区域外表面的信息，因此三维非结构化网格数值模拟计算结果可视化快速实现问题就转化为快速的判断在三维网格中哪些组成单元的面是计算域外表面的问题。

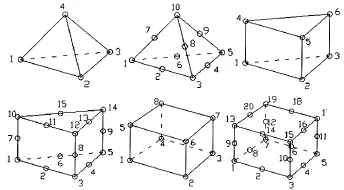
图1 常见的网格形式

2 非结构化网格的基本定义

在说明算法以前我们先有如下的定义:

定义1:F为在区域D中面的集合，对于任意一个面f∈F，如果f同属于两个不同的单元，则f属于内部面，记为I。如果f只属于唯一单元，则f属于外部面，记为Г。I∪Г=F。

定义 2:f∈F，v1，v2，……，vL是面 f的顶点，记为 f=如果f的顶点的排列符合顺时针排列，f称为顺时针面。

3 两种判断外边界的算法

3.1 传统算法

传统搜索外边界面的算法是对所有单元的面进行提取，进而按所提取的面进行循环，搜索出循环到的面是否在已提取的集合中有相同的面，若有重复则说明此面是内部面，否则此面为外部面[2]。

步骤1:

从每个单元中提取面元，使每个面顶点的排序满足定义2，Sj为单元ej所包含的面的个数，通过对一个单元的面元的提取，形成单元ej中面的集合Fj={f(1)j，f(2)j，……fsjj}，而每个面记为 f(s)j={njm1，njm2，……，njnks}。其中 j=1，2，……，Me;njmk∈ej⊂Np(Np为所有点的集合)，s=1，2，……，S，k=1，2，……，Ks。Ks为平面f(s)j的顶点数。非结构化网格中所有单元所包含的面记为F={Fj|j=1，2，……，Me}。

步骤2:

逐个对比F中的元素，区分出外部面集合Г和内部面集合I。因为同一个单元没有重复面，若一个面在集合F中出现两次，则说明为两个单元共有，为内部面。若只出现一次，则为外部面。此过程可用以下方程表示:

对于 1≤j≤Me-1，1≤k≤sj，如果，那么就存在 i0＞ j，1≤s0≤si0，满足，因此反之，如果，那么

当第二步结束后，在非空集合F中就提取出外表面的集合Г。

3.2 改进算法

改进后的算法是按节点对单元的面进行提取，找出最小(或最大)顶点序号相同的一组面元进行提取形成集合，并判断这些集合中的面元是否有重复，若有重复则说明此面是内部面，否则此面为外部面。

步骤1:

找出与结点ni(ni∈Np)相关联的面，且ni是这个面结点序号最小的值，这些符合条件的面形成矩阵Eni，Eni中的每个元素是满足以上条件的面除ni外其它结点序号的集合。

步骤2:

逐个对比Eni中的元素，定义，如果有，那么就存在 j0≠k(j0＞ k)，使，那么}一定是内部面，保存在集合I中。如果且，那么平面{ni，nl1，nl2，……，nlk}一定是外部面，保存在集合Г中。

步骤3:

k=k+1，如果k＜kni，那么重新执行第二步，并且把内部面和外部面分别记录在集合I和Г中。如果k=kni，那么执行第四步。

步骤4:

i=i+1，如果i≤N，那么重复执行1-3步，把新判断的面加到集合I和Г。如果i＞N，则判断结束，其中N为Np中点的个数。

4 两种算法的实例比较

传统算法中对外边界判断计算次数是O(M2e)，而利用改进算法需要的计算次数是O(N)，一般来说Me和N是同一个量级，因此改进算法的计算次数要远远小于传统算法。

我们应用一个实际的例子来比较两种算法的运算速度:

铁成尾矿库隶属于河北省承德市滦平县小营乡管辖，尾矿库库区最高海拔高程900 m，最低海拔高程410 m，总面积约为109万m2。

计算区域网格由ansys划分，为四面体、六面体混合网格，共160523个节点，739987个单元，图2为计算网格局部图。计算平台为CPU P4 2.4G，1G内存，编程环境为VS.Net 2005，表1为计算结果，结合自行开发的基于OpenGL的流体力学可视化软件，采用Dividing Cube等值面填充的方法显示计算区域的含水度，将结果动态显示出来，见图3。通过表1可知通过算法的改进大大提高了显示效率。