大尺度区域控制灌溉水稻需水量的空间变异分析

2010-06-26郭龙胜周光涛

黑龙江水利科技 2010年1期

郭龙胜，周光涛

(黑龙江省水利水电勘测设计研究院，哈尔滨 150080)

1 引言

控制灌溉处理为只有当现场观测的土壤水分在达到下限土壤含水量时，才能灌水至上限，灌水后田面不保留水层。遇降大雨，田间可蓄雨水(分蘖后期除外)，但蓄水不超过50 mm。控Ⅰ区完全按控灌标准灌水，控Ⅱ区在遇低温冷害(返青期最低温度降至3℃以下，拔节孕穗期最低温度低于15℃)时灌水保温，田间保留与常规灌溉相同的水层。该方法在黑龙江已大面积推广应用，具体指标如下:

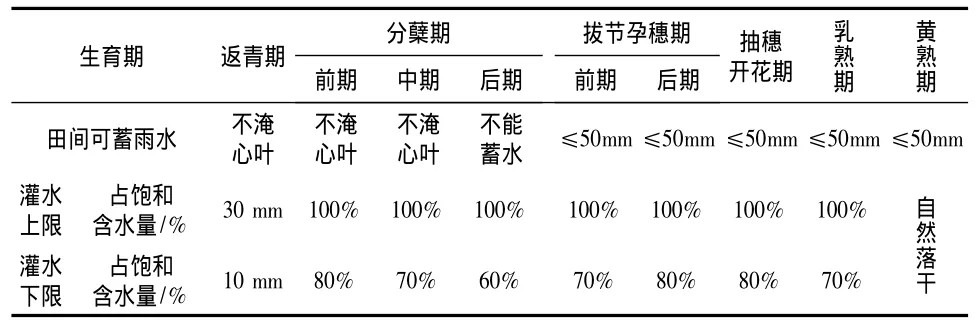
表1 控灌水稻生育阶段根层土壤水分控制标准

以往研究结果表明，不论在大尺度上还是在小尺度上，控制灌溉水稻需水量均表现为高度的空间异质性现象。控制灌溉水稻需水量空间分布的异质性，降低了需水量分布状态的可预知性，增加了水稻需水量研究时取样点设置的难度。在进行需水量研究时，经常采用的方式是增加取样点的数目，但此时面临的两个突出问题是如何量化取样点的数目以及如何进行空间取样点的布设。理想的方法是无限制的增加取样点数目直至把研究系统的全部需水量测出，此法的操作性很差，但能否采用一种类似于空间上无限取样的方法，利用有限的取样点数据，结合取样点位置的信息较合理的对需水量进行估测?地统计学中的克里格内插法结合定积分的方法可能为解决此类问题提供帮助，克里格内插法是一种类似于空间上无限增加取样点数目的方法。它是以区域化变量理论(需水量可作为区域化变量)为基础，利用变异函数分析结果提供的空间结构信息，依据待估样点周围已抽样测定的数据，充分考虑待估点与邻近样点的空间位置关系，对空间上未取样点的数据进行线性无偏最优估计的方法。本文针对克里格内插法的估测值所进行的检验结果表明，该方法能够用于进行水稻全省范围内未取样点位置处的需水量的估计。为了得到研究区的需水量，利用克里格插值方法所估计出的各个空间位置处的需水量(均为离散变量)，通过建立空间位置坐标与需水量之间的相关方程，发现对二者之间关系拟合程度最高的方程为线性模型，利用该模型，采用定积分的方法(积分区间为计算单元的大小)从而求出不同控制灌溉模式水稻的需水量。

2 变异函数理论模型最优拟合

根据理论变差函数曲线的拟合情况及有关统计检验结果，选择适当的半变异函数模型、直到得出理想的理论变差函数为指数函数，模型参数见表2。

表2 控制灌溉需水量理论变差函数检验

对需水量所进行的理论模型拟合结果表明模型最低拟合决定系数R2=0.8935，拟合程度很好。控灌1和控灌2水稻需水量空间分布均达到显著水平，空间变异性明显。其空间变异模型系数见表3。

由于符合指数模型，需水量空间自相关范围是模型范围参数，因此控灌1和控灌2水稻需水量空间自相关范围分别是29.10 m和29.14 m。

3 水稻控制灌溉需水量空间插值

3.1 控制灌溉水稻需水量克里格插值结果检验

利用研究区内7个试验点的需水量实测数值，验证半方差分析基础上所进行的克里格插值方法对该区域水稻需水量的估计效果。非参数统计的成对样本的符号检验结果表明，控灌1条件下7个采样点各自对角线下方10 000m×10 000m样方内的需水量的估测值与实测数值之间差异不显著，表明克里格插值方法能够用于对控制灌溉1水稻需水量的估计，而对控灌2克里格可能不是适当的插值方法。

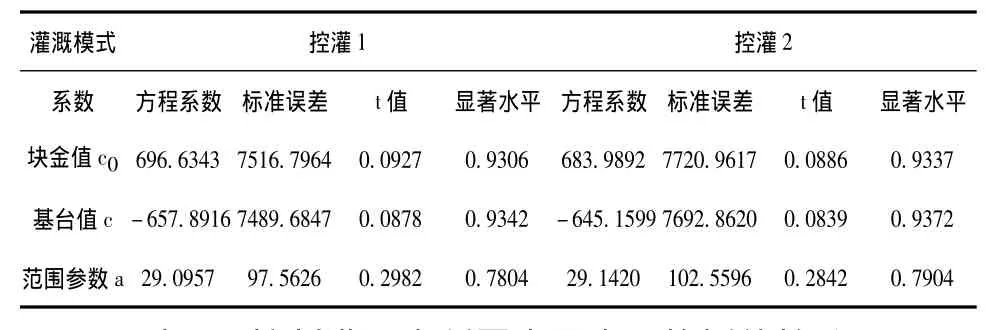
表3 控制灌溉需水量空间变异系数

表4 控制灌溉水稻需水量克里格插值检验

3.2 控制灌溉水稻需水量的克里格估计

由表5可以看出，对于控灌2，依据样地内所有取样点(n=7)的需水量的平均值所换算出的每公顷水稻田表层需水量之间存在较大的差异(最大为17.71 mm/hm2)，而控灌1在此方面却存在较小的差异(最大为17.46 mm/hm2)，说明随着取灌溉模式的不同，水稻需水量的估计值之间也存在一定的误差。

本研究根据7处不同的试验点，在整块样地范围内各空间位置处的估测值与其相应坐标之间的关系，采用线性模型能较好的拟合，说明指数模型能反映需水量估测值与其空间位置之间的关系。控制灌溉水稻需水量的克里格插值方法估测结果表明，控灌1的需水量估测值与全部样点平均值所推算出的需水量相差较大，说明对于控灌1，说明7个取样点的数据可能未能正确反映水稻的需水量，需要继续增大取样点的数目。控灌2克里格插值方法估测结果与全部样点平均值所推算出的结果较近似，7处取样点的数据已能较为准确的反映水稻的需水量。

表5 控制灌溉水稻需水量克里格插值残差分析

4 黑龙江省水稻控制灌溉需水量空间变异性分析

5 结论

以上2种灌溉模式的水稻需水量的变异函数曲线理论模型均为指数模型，空间变异主要是由结构性因素引起，且空间自相关程度均属中等以上。控灌1、控灌2水稻需水量的空间变异尺度分别为4.17和5.56 m;非参数统计的成对样本符号检验结果表明，变异函数分析结果基础上的克里格内插法适用于水稻需水量的估计。利用此估计值，拟合其与位置坐标值之间的关系均为线性模型;在本次调查的范围内，控灌2条件下水稻需水量与实测值近似相等(p=0.22)，空间关联紧密;采用地统计学的克里格空间插值，结合线性回归和定积分的方法，可以实现水稻需水量的准确估计。