斯穆里安合并记法的一种变形

熊 明

（华南师范大学政治与行政学院，广东广州510631）

斯穆里安合并记法的一种变形

熊 明

（华南师范大学政治与行政学院，广东广州510631）

公式按照其语义特征可被合并为实质蕴涵型公式和荒谬蕴涵型公式，由此任何一个公式都可被分解为前件和后件两个部分。这一合并简化了斯穆里安著名的合并记法。就这一新的合并记法，提出了两种结构归纳证明，建立了一个希尔伯特型古典逻辑系统，并证明其完全性。

公式；斯穆里安合并记法；结构归纳法；实质蕴涵；荒谬蕴涵

一、斯穆里安的合并记法

在命题逻辑中，出于某种目的（例如对称性）在规定公式时会引入较多的联接词符号。例如，可按下面的方式给出公式：

（1）命题变元p1，p2，p3，…，pn，pn＋1，…（n∈N）是公式。

（2）如果α是公式，那么¬α也是公式。

（3）如果α和β是公式，那么（α∧β）、（α∨β）、（α→β）、（αβ）、（α↔β）、（αβ）也都是。

（4）只有通过上述规则得到的符号串才是公式。

这里引入了多达七种联接词符号（其中“”称为荒谬蕴涵）来规定公式。这样，不论是在运用结构归纳证明法进行证明，还是运用结构归纳的定义法进行规定，除了命题变元的情况之外，我们尚有七种情况需要分别讨论。这就使得整个讨论的工作量较大。以结构归纳证明为例，它的施行如下。如果下列条件成立，那么任何公式α都有性质F：

①对任何命题变元π，π都有性质F。

②若公式α有性质F，则公式¬α也有性质F。

③若公式α和β有性质F，则公式（αθβ）也有性质F，其中θ∈｛∧，∨，→，，↔，｝。

下面把它称为公式的“第一结构归纳证明法”。比如，在对公式进行解释时，我们必须分下列七种情况归纳定义公式的真值：

设α、β、γ是公式，如果函数V：Form（PL）↦｛0，1｝（0表示真，1表示假）满足如下条件，则称之为PL－赋值（以下简称“赋值”）：

（1）V（¬α）＝0，当且仅当V（α）＝1。

（2）V（α∨β）＝1，当且仅当V（α）＝1，V（β）＝1。

（3）V（α∧β）＝0，当且仅当V（α）＝0，V（β）＝0。

（4）V（α→β）＝1，当且仅当V（α）＝0，V（β）＝1。

（5）V（αβ）＝0，当且仅当V（α）＝1，V（β）＝0。

（6）V（α↔β）＝0，当且仅当V（α）＝V（β）。

对公式α和β，如果对任何赋值V，都有V（α）＝V（β），那么就称α与β逻辑等值，记为α⇔β。

为达到简化的目的，可考虑按照公式的某种特征把多种公式合并成为一类公式，使得全体公式被分为数目较少的几类。故而既能简化结构归纳证明，又能简化结构归纳定义。

例如，可把除单式和形如¬¬α的公式之外的公式按其形式首先分成以下几类：

（1）形如（α∨β）的公式 （1*）形如¬（α∨β）的公式

（2）形如（α∧β）的公式（2*）形如¬（α∧β）的公式

（3）形如（α→β）的公式（3*）形如¬（α→β）的公式

（4）形如（αβ）的公式（4*）形如¬（αβ）的公式

（5）形如（α↔β）的公式（5*）形如¬（α↔β）的公式

不难看出，上面的公式或者逻辑等值于某个析取式，或者逻辑等值于某个合取式，并且不论是析取式的析取支，还是合取式的合取支都比原来的命题在结构上要简单一些。有下面已证明的逻辑等值式为证：

（1）α→β⇔¬α∨β，αβ⇔¬α∧β

（3）¬（α∧β）⇔¬α∨¬β，¬（α→β）⇔α∧¬β

（4）¬（αβ）⇔α∨¬β，¬（α→β）⇔α∧¬β

这样可把除单式和形如¬¬α的公式之外的公式进行合并，分成两个大类。具体而言，一类是形如（α∨β），（α→β），（αβ），¬（α∧β），¬（α↔β），¬（αβ）等的公式，可称它们为析取型公式。另一类是形如（α∧β），（αβ），（α↔β），¬（α∨β），¬（α→β），∧（αβ）等的公式，可称它们为合取型公式。下面把这两类公式统称为有型公式。对任意一个有型公式γ，规定它的成分γ1和γ2如表1所示。

析取型公式和合取型公式的语义特征复述如下：当γ是析取型公式时，γ⇔（γ1∨γ2）；当γ是合取型公式时，γ⇔（γ1∧γ2）。

根据上述合并，公式无非有单式、形如的¬¬α的公式、析取型公式及合取型公式四类，据此可以提出与公式的第一结构归纳证明法类似的归纳证明法（称之为“第二结构归纳证明法）如下。如果下列条件成立，那么任何公式α都有性质F：

①对任何单式α，α都有性质F。

②若公式α有性质F，则公式¬¬α也有性质F。

③若对析取型公式α，α1和α2都有性质F，则公式α也有性质F。

④若对合取型公式α，α1和α2都有性质F，则公式α也有性质F。

表1

显然，在对公式施行第二结构归纳证明时，只需要验证四种情形，这在一定程度上降低了结构归纳的繁琐度。以上合并记法由逻辑学家斯穆里安首先提出，所以被称为“斯穆里安的合并记法”。［2］21它的比较系统的阐述可参见相关论著［1］20－22。在本文中，我们要就这一记法展开两个方面的讨论：一是指出这一记法本身还可进一步降低结构归纳的繁琐度；二是仿照这一记法，给出另一种类似的记法。

二、斯穆里安合并记法的一点改进

在斯穆里安记法中，形式¬¬α的公式没有被看作是有型公式，施行结构归纳的时候，要单独对这种形式的公式进行证明。现在证明，这种公式可以并入到有型公式之中。首先，注意下面的等值式：

因而可把形如¬¬α的公式并到析取型公式和合取型公式任何一类中，并规定它的成分γ1和γ2都为α。这一做法改进了斯穆里安原来的记法，是因为能够证明以下论断：

如果下列条件成立，那么任何公式α都有性质F：

①对任何单式α，α都有性质F。

②对任何析取型公式α，若α1和α2有性质F，则α也有性质F。

③对任何合取型公式α，若α1和α2有性质F，则α也有性质F。

证明：对任何公式α，对任何非负整数n，我们规定¬nα满足：¬0α＝α且¬n＋1α＝¬（¬nα）。为证任何公式α都有性质F，我们对α运用第一结构归纳法加强证明：对任何公式α，对任何非负整数n，¬nα都有性质F。

首先，当α是命题变元π时，对n运用数学归纳法证明：对任何非负整数n，¬nπ有性质F。n＝0或1时，¬nπ即π或¬π按条件①自然有性质F。当n＝k（k≥2）时，由于（¬nπ）1＝¬k－2π，（¬nπ）2＝¬k－2π，由（数学归纳法的）归纳假设¬k－2π有性质F，于是按②（或③），¬nπ也有性质F。

当α是公式¬β时，对任何非负整数n，都有¬nα＝¬n＋1β。所以，从结论：对任何非负整数n，¬nβ有性质F，立有：对任何非负整数n，¬nα有性质F。

当α是公式（β∨γ）时，首先注意，（¬0α）1＝β，（¬0α）2＝γ；（¬1α）1＝¬β，（¬1α）2＝¬γ。按（第一结构归纳法的）归纳假设，β、γ、¬β、¬γ已有性质F，所以，根据②和③，¬0α和¬1α都有性质F。

其次，当n＞1时，（¬nα）1＝¬n－2α，（¬nα）2＝¬n－2α。接下来，对n施行数学归纳法证明：若n＞1，则¬nα也有性质F。当n＝2时，（¬nα）1＝¬0α，（¬nα）2＝¬0α。而前面已证¬1α和¬0α都有性质F，根据②（或③）就有¬2α也有性质F。当n＝k（k＞2）时，（¬nα）1＝¬n－2α，（¬nα）2＝¬n－2α。由归纳假设，¬n－2α有性质F，于是，¬nα也有性质F。

当α是公式（β∧γ）、（β→γ）、（βγ）时，类似上面可证。还有α是公式（β↔γ）、（βγ）两种情况需要考虑。下面分析α是公式（β↔γ）的情况，α是（βγ）的情况类似进行。注意到α1＝（β→γ），α2＝（γ→β），由归纳假设，β、γ已有性质F，再根据α＝（β→γ）和α＝（γ→β）两种情况中的证明，可知（β→γ）和（γ→β）也有性质F。这样，按条件③，¬0α＝α有性质F。类似可证¬1α＝¬α也有性质F。对¬nα（n＞2）情形类似α＝（β∨γ）中相应情形的证明，此略去。

综合上面所述，可以断定对任何公式α以及任何非负整数n，公式¬nα都有性质F。这就达到了证明的目的。

三、斯穆里安合并记法的一种新变形

根据先前对公式的真值的规定，容易证明下面的逻辑等值式：

（1）¬¬α⇔（¬α→α），¬¬α⇔（¬αα）

（2）（α∨β）⇔（¬α→β），（α∧β）⇔（¬αβ）

（4）¬（α∧β）⇔（α→¬β），¬（α∨β）⇔（α→¬β）

（5）¬（α→β）⇔（β→α），¬（α→β）⇔（β→α）

可以发现，任何公式都或者可以逻辑等值地转化为实质蕴涵式，或者可以逻辑等值地转化为荒谬蕴涵式，而且在这些蕴涵式中前后件位置出现的公式比原来的公式要简单。于是，可把形如（α∨β），（α→β），（αβ），¬（α∧β），¬（αβ），¬（α↔β）的公式合并为一类，称之为实质蕴涵型公式。把形如（α∧β），（αβ），（α↔β），¬（α∨β），¬（α→β），¬（αβ）的公式并为一类，称之为荒谬蕴涵型公式；对这些公式，规定它们各自的前件和后件如表2所示。

利用上面给出的逻辑等值式，我们不难证明这两类公式与它们各自的前后件有下面的关系：当γ是实质蕴涵型公式时，γ⇔（γ1→γ2）；当γ是荒谬蕴涵型公式时，γ⇔（γ1γ2）。

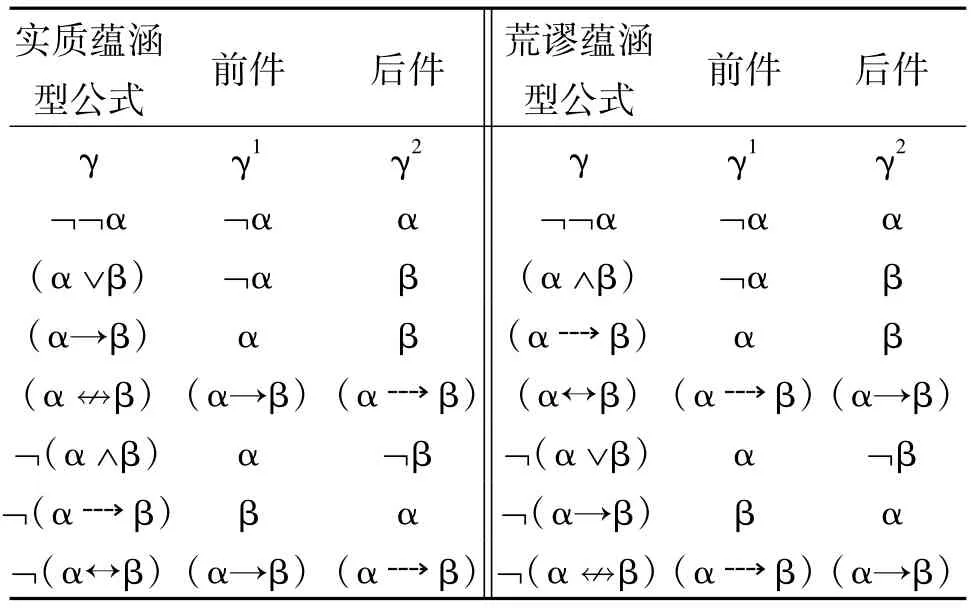
表2

以上合并比斯穆里安原先的合并记法更精简的地方在于，双重否定式也被进行了合并。注意，双重否定式既可归入实质蕴涵型公式，又可归入荒谬蕴涵型公式。

根据以上对公式的分类，有公式的第三结构归纳证明法，其原理如下。如果下列条件成立，那么任何公式α都有性质F：

①对任何单式α，α有性质F。

②对任何实质蕴涵型公式α，若α1和α2有性质F，则α也有性质F。

③对任何荒谬蕴涵型公式α，若α1和α2有性质F，则α也有性质F。

在采用荒谬蕴涵型和实质蕴涵型这种合并记法时，还可再给出一种新的结构归纳证明法和定义法，无妨以“第四”来命名之，其原理如下。如果下列条件成立，那么任何公式α都有性质F：

①对任何单式α，α都有性质F。

②对任何实质蕴涵型公式α，若¬α1和α2有性质F，则α也有性质F。

③对任何荒谬蕴涵型公式α，若¬α1和α2有性质F，则α也有性质F。

这里利用第一结构归纳证明法证明第四结构归纳证明法的合理性。

为证任何公式α都有性质F，对α运用第一结构归纳法加强证明：对任何公式α，对任何非负整数n，¬nα都有性质F。

首先，当α是命题变元π时，对n运用数学归纳法证明：对任何非负整数n，¬nπ有性质F。n＝0或1时，¬nπ即π或¬π按条件①自然有性质F。当n＝k（k≥2）时，由于（¬nπ）1＝¬k－1π，（¬nπ）2＝¬k－2π，由（数学归纳法的）归纳假设¬k－1π和¬k－2π都有性质F，于是按②（或③），¬nπ也有性质F。

当α是公式¬β时，对任何非负整数n，都有¬nα＝¬n＋1β。所以，从结论：对任何非负整数n，¬nβ有性质F，立有：对任何非负整数n，¬nα有性质F。

当α是公式（β∨γ）时，此时，（¬0α）1＝¬β，（¬0α）2＝γ；（¬1α）1＝β，（¬1α）2＝¬γ；（¬nα）1＝¬n－1α，（¬nα）2＝¬n－2α（n＞1）。按（第一结构归纳法的）归纳假设，β、γ、¬β、¬γ已有性F，所以，根据②和③，¬0α和¬1α都有性质F。

接下来，对n施行数学归纳法证明：若n＞1，则¬nα有性质F。当n＝2时，（¬nα）1＝¬1α，（¬nα）2＝¬0α。前面已证¬1α和¬0α都有性质F，根据②（或③）就有¬2α也有性质F。当n＝k（k＞2）时，（¬nα）1＝¬n－1α，（¬nα）2＝¬n－2α。由归纳假设，¬n－1α和¬n－2α都有性质F，于是，¬nα也有性质F。

当α是公式（β∧γ）、（β→γ）、（β→γ）时，类似上面可证。还有α是公式（β↔γ）、（βγ）两种情况需要考虑。下面分析α是公式（β↔γ）的情况，α是（βγ）的情况类似进行。注意到α1＝（β γ），α2＝（β→γ），由归纳假设，β、γ、¬β、¬γ已有性F，再根据α＝（β→γ）和α＝（βγ）两种情况中的证明，可知（β→γ）和（βγ）也有性质F。这样，按条件③，¬0α＝α有性质F。类似可证¬1α＝¬α也有性质F。对¬nα（n＞2）情形类似α＝（β∨γ）中相应情形的证明，此略去。

综合上面所述，可以断定对任何公式α以及任何非负整数n，公式¬nα都有性质F。这就达到了证明的目的。

类似地，通过加强证明：对任何公式α，α和¬α都有性质F，就可获得第三结构归纳证明法的合理性，具体证明略去。

四、新合并记法下的逻辑系统

在斯穆里安的合并记法下，常规的希尔伯特逻辑系统、自然推演逻辑系统等都可以得到比较优雅的表达。文献［1］、［2］、［3］都给出了这样的系统。这里借助新合并记法，建立一个新的希尔伯特逻辑系统。有关的公理模式和推演规则如下：

（D1）α→β→α

（D2）（α→β→γ）→（α→β）→（α→γ）

（D3）¬α1→α，其中α是实质蕴涵型公式。

（D4）（¬α1→γ）→（α2→γ）→（α→γ），其中α是实质蕴涵型公式。

（D5）α→¬α1，其中α是荒谬蕴涵型公式。

（D6）α→α2，其中α是荒谬蕴涵型公式。分离规则（MP）：对任何公式，从α和α→β可得到β。

设∑是公式集，α是公式。按通常方式定义推演关系├，具体定义略去。这就规定了一个演绎系统，它对于古典后承关系是完备且健全的。下面用“∑⊨α”表示α是∑的后承，即对任何满足V（∑）＝0的赋值V，都有V（α）＝0。健全性和完备性的表述为：∑├α，当且仅当∑⊨α。

“仅当”情形即健全性是容易证明的，下面只证明“当”情形即完全性。为证明完全性，先在新合并记法下完成所谓“命题逻辑基本定理”的表述和证明。先给出两个概念：可满足性与和谐属性。

对于公式α，如果存在赋值V，使得V（α）＝0，那么就称α是可满足的。对于公式集∑，如果存在赋值V，使得V（∑）＝0，即任意公式α∈∑，都有V（α）＝0，那么就称∑是可满足的。设C是公式集构成的集簇，称C是和谐属性，如果C中的任何公式集∑都满足下列条件：

（1）对任意命题变元π，π和¬π不都属于∑。

（2）对任意实质蕴涵型公式α，若α∈∑，则∑∪｛¬α1｝∈C，∑∪｛α2｝∈C至少有一成立。

（3）对任意荒谬蕴涵型公式α，若α∈∑，则∑∪｛¬α1，α2｝∈C。

命题逻辑的基本定理说的是：如果C是和谐属性，那么C中的任何公式集都是可满足的。这建立和谐属性与可满足性之间的关系，沟通了命题逻辑的语形和语义关系。

为证明该定理，还需要几个概念。设C是公式集构成的集簇。如果C中公式集的任何子集都还在C中，那么就称C是子集封闭的。如果∑∈C，当且仅当∑的任何有穷子集都属于C，那么称C是有有穷特征的。设Γ∈C，如果没有任何公式集∑∈C，使得Γ⊂∑，那么就称Γ在C是极大的。

由于C是和谐属性，容易把它扩充成具有有穷特征且子集封闭的和谐属性C＋。任取S∈C，枚举全体公式如下：α1，α2，…，αn，…（n∈N），藉此对n∈N进行归纳定义公式集Sn如下：S1＝S，并且若Sn∪｛αn｝∈C＋，则Sn＋1＝Sn∪｛αn｝，否则Sn＋1＝Sn。显然，对任意n∈N，都有Sn⊆Sn＋1，且Sn∈C＋。

令Sω＝｛α｜存在n∈N，使得α∈Sn｝。易见，Sω是S的一个扩充。利用C＋的有穷特征性易证：Sω∈C＋，再利用C＋的子集封闭性可证：Sω是具有C＋中的极大元。下面证明Sω可满足，从而就证明了S可满足。

构造赋值Vω满足条件：对任何命题变元π，Vω（π）＝0，当且仅当π∈Sω。下面运用公式的第四结构归纳证明：对任何公式α，如果α∈Sω，那么Vω（α）＝0。

当α是单式时，若α＝π∈Sω，则Vω（α）＝0；若α＝¬π∈Sω，则π∉Sω，于是，Vω（π）＝1。这样，Vω（α）＝Vω（¬π）＝0。

当α是实质蕴涵型公式时，设α∈Sω，则Sω∪｛¬α1｝∈C＋，Sω∪｛α2｝∈C＋至少有一成立。由于Sω在C＋极大，所以，¬α1∈C＋，α2∈C＋至少有一成立。则由归纳假设，Vω（¬α1）＝0（即Vω（α1）＝1），Vω（α2）＝0至少有一成立。于是，就有Vω（α1→α2）＝0，所以，Vω（α）＝0。

当α是荒谬蕴涵型公式时，设α∈Sω，则有Sω∪｛¬α1，α2｝∈C＋，又由Sω在C＋极大，知¬α1和α2都属于C＋。则由归纳假设，有Vω（¬α1）＝0（即Vω（α1）＝1），Vω（α2）＝0。于是，就可得到Vω（α）＝Vω（α1α2）＝0。至此，完成了命题逻辑基本定理的证明。

现在可证完全性。首先由公理（D1）和（D2）以及规则MP可证演绎定理成立：若∑∪｛α｝├β，则∑├α→β。然后，相对于某个公式α，如果公式集∑满足∑α，那么就规定∑是α－和谐的。下面证明所有的α－和谐公式集构成的集簇是和谐属性。设∑是α－和谐公式集，验证∑满足和谐属性的各个条件。首先，∑中不会含某个命题变元π及其否定¬ π。不然，则∑├π以及∑├¬π。但公理（D3）的一个特例是¬π→π→α，由此运用演绎定理及分离规则可得∑├α。这与∑是α－和谐公式集矛盾。

设实质蕴涵型公式β∈∑，要证∑∪｛¬β1｝，∑∪｛β2｝至少有一个是α－和谐公式集。假设不然，则有∑∪｛¬β1｝├α，∑∪｛β2｝├α。由公理（D4）、演绎定理以及分离规则可证∑├α，这与∑是α－和谐公式集矛盾。

再设荒谬蕴涵型公式β∈∑，要证∑∪｛¬β1，β2｝是α－和谐公式集。假设不然，则有∑∪｛¬β1，β2｝├α。由公理（D5）、（D6）、演绎定理以及分离规则可证∑├α，这又与∑是α－和谐公式集矛盾。

上面证明了所有的α－和谐公式集构成的集簇是和谐属性，由命题逻辑的基本定理知α－和谐公式集是可满足的。最后，假设∑α，则∑∪｛¬α｝就是α－和谐公式集。因为若∑∪｛¬α｝├α，就可由公理（D3）（取特例：¬α→α→α）得出∑├α。于是∑∪｛¬α｝是可满足的。这就得到了∑⊭α。完全性至此得证。

［1］ FITTING M.First－Order Logic and Automated Theorem Proving.New York：Springer－Verlag，1990.

［2］ SMULLYAN R.First－Order Logic.Berlin：Springer－Verlag，1968.

［3］ 胡泽洪.蕴涵刍议.华南师范大学学报：社会科学版，2006（5）：1－6.

［4］ 王健平.实质蕴涵与自然语言中的相关蕴涵命题分析.华南师范大学学报：社会科学版，2005（3）：11－18.

［5］ 熊明.古德曼悖论与形式的归纳逻辑系统.华南师范大学学报：社会科学版，2003（5）：28－34.

［6］ 张清宇.古典命题逻辑的证伪系统.自然辩证法研究，1996（增刊）：4－6.

【责任编辑：赵小华】

B813

A

1000－5455（2010）03－0107－05

2009－11－08

广东省优秀青年创新人才培育项目（WYM08064）；教育部人文社会科学重点研究基地重大项目“现代逻辑背景下的逻辑哲学问题研究“（07JJD720045）

熊明（1973—），男，云南昭通人，华南师范大学政治与行政学院副教授。