感应式电能计量仪表的电网谐波影响及其解决方法研究
2010-06-23郝云飞
郝云飞
(冀中能源邢矿化工项目筹备处,河北 邢台 054000)
1 引言
随着电力电子技术在电力系统中的广泛运用,电力谐波对电子测量仪器的影响问题也日益严重。由于电力系统中所应用的电子测量设备对于电力系统的谐波具有较高的敏感度,因而对电力系统电能测量仪的电网谐波影响的研究具有重要的实践意义。电能计量仪表是用来对电网输送的经济量进行核算的重要设备,其测量的精度直接影响到电力系统输、发电双方的经济效益。另一方面,作为国民经济核算的重要依据,电能的计量的精度将间接影响到国家经济政策的制定。
目前,市场上广泛采用的电子式电能表是结合感应式电能表和电子部件的电能测量仪表,其测量的主要工作元件是感应式电能测量构件[1]。测量的基本原理是利用传感器来完成电能到脉冲信号的转换,在经由电子电路将脉冲信号进行相应处理后从而来实现对电能大小的测量。尽管一些电能表的设计及生产企业不断改进其技术性能,并试图规避感应式测量机构作为其主要测量部件所存在的缺陷,但目前仍未改变感应电能表所存在的准确度偏低以及适用频率范围偏窄的缺点。
2 感应式电能表的结构及工作原理
2.1 感应式电能表的结构组成
感应式电能表的主要结构分为测量构件以及辅助构件两大部分,测量构件是感应式电能表的核心部分,由驱动元件、转动元件、制动元件、上下轴承以及记度器组成[2],结构如图 1所示。驱动元件的主要部分由电压及电流互感器构成,其作用在于当交流电压及电流所产生的磁通穿过计量器的圆盘时,与转盘中的感应电流相互作用构成力矩,驱动指针转动;转动元件则由转盘以及转轴两部分构成,其主要作用在于当穿过圆盘的电流与磁通产生转动力矩时,驱动转轴连续动作;制动元件主要由一块永磁体与调整装置构成,其中永磁体是采用具有较大的矩弯力和剩磁感应强度的合金材料制作而成,当转盘在上文所述的力矩下开始转动时,开始切割永磁体产生的磁力线的运动,这使得转盘的转动速度与其被指示的功率成正比变化;轴承主要起到支撑作用的金属构件,同时考虑到需要减小机械运动过程因素的,轴承质量的好坏将直接影响到测量精度与电能表的使用寿命;计度器又称积算机构,其主要作用在于计量转盘所转动的圈数,并依次显示出所测定的电能数量,目前使用的计度器分为字轮式和指针式两种[3]。
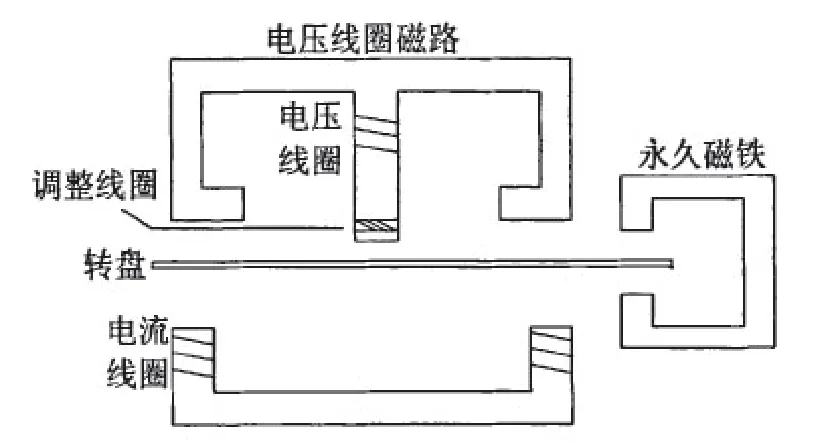
图1 感应式电能表基本结构图
2.2 感应式电能表的工作原理
在利用感应式电能表进行测量时,电压线圈两端的电压即为被测电压U,流过电流线圈的电流为iL。由于电压线圈的匝数较多,且磁路间的间隙过小,所以其产生的自感也较大,电压线圈产生的磁通为uφ要滞后于电压U 90度;相对而言,电流线圈的匝数较少,磁路间隙较小,因而电流线圈所产生的磁通iφ与电流iL同向。由电压线圈和电流线圈中产生的交变磁通穿过转盘时,产生感应电流,并与电压磁通及电流磁通相互作用产生转动力矩MQ。
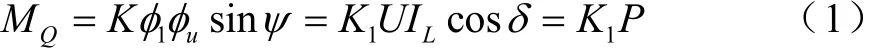
在上述描述转动力矩的计算公式中,考虑到铁芯和转盘的尺寸,以及二者之间的相对位置等因素,由K、K1分别表示其影响系数,电压磁通落后于电流磁通的相位角以Ψ来表示,电压与电流之间的相位角差以σ表示,而所测量电力系统中负载消耗的有功功率则以 P来表示。根据式(1)中描述的计算模型,显然电能表转盘转动的力矩与系统负载的功率成正比。当系统的负载功率一定时,转盘所受到的驱动力矩固定不变,一旦驱动力矩大于转盘系统的固有摩擦阻力,转盘将处于加速转动状态,此时测量数据出现偏差。考虑到加速度的影响,在设计转盘系统时,在表盘下方加装一个永磁体,依次对加速转动的变盘起到制动作用,制动的力矩 Mr如式(2)所示。其中,转盘的转速与转动力臂分别以n和hr表示,转盘的制动磁通以及制动力矩分别以Φr和Kr表示。转盘转动平衡条件为MQ=Mr,在此条件基础上,可以轻易推得在时间T内,系统中负载所消耗的电能W的表达式,如式(3)所示。在式(3)中,负载消耗的功率 P与转盘的转动速度n呈正比,其中由平衡条件可以推得 K1P=k2n。
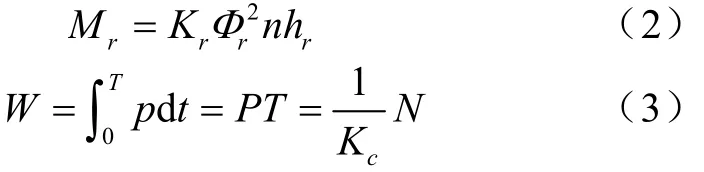
3 考虑谐波影响因素的电能表计量数序模型
3.1 模型建立的前提条件
畸变谐波对感应式电能表的计数影响主要取决于实际谐波的特征情况以及电能表自身的特性[4]。由于影响到电能表测量准确度的因素较多,其作用于电能表的功能机理较复杂,不同生产企业或不同生产批次的产品间,其测量的特性都会有较大出入。另一方面,目前国内有关谐波对电能表影响的研究不在少数,但大都研究都忽略了磁路的饱和,或者忽略了调整线圈的作用。
3.2 模型设计过程中考虑的影响因素
针对以上缺点和不足,模型建立规避了过往研究的种种弊病,将线圈磁路的饱和影响、调整线圈的作用以及频率对电压线圈和圆盘参数的影响纳入考虑范围内。考虑到以上影响因素,这里我们将建立畸变波形对感应式电能计量仪表误差影响模型,并将其主要影响因素纳入考虑范围,将模型建立在下列假设条件:
(1)流经电能表电压线圈与电流线圈的电流与工作磁通相等。
(2)忽略直流分量。
(3)不考虑轻载补偿装置的影响。
3.3 感应式电能表模型建立
电网谐波对电能表计量仪表的影响是建立在电能表的频率特性曲线基础上的,电能表频率特性曲线的特性对其在谐波功率影响下的计数具有较大的影响[5]。式(4)是建立在额定参数基准上的电能表频率模型表达式。其中,取定电能表的额定电压及额定电流分别为u(t)与i(t),电压与电流的幅值分别为Um与Im,电流的角速度与相位角分别为ω与θi表示。
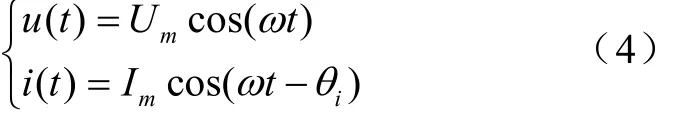
当将基波与谐波进行叠加时,考虑谐波因素的电压与电流的表达式如式(2)。其中,基波与谐波的电压幅值、电流幅值分别为Uh与Ih,电压与电流的初相角分别为θuh与θih,角频率以ωh表示。
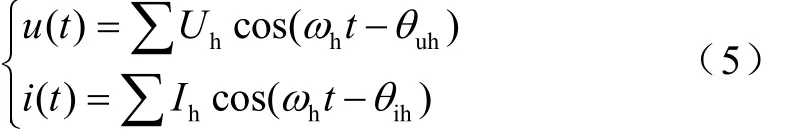
式(5)描述了电压及电流线圈中电流所产生的主磁通。其中
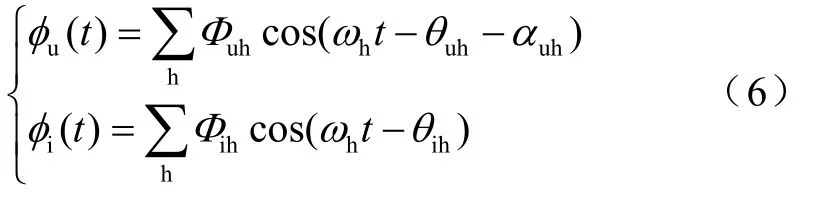
电能表的计量误差的频率特性计算模型如式(5)。其中由于谐波作用所产生的磁通如式(6)所示。
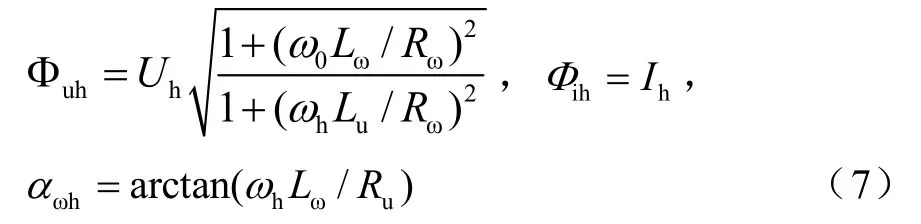
这里,将磁路饱和因素纳入考虑范围内,其有效磁通与主磁通之间的非线性关系如式8所示。其中,磁路的各饱和系数分别以αu1、αu3、αu5、i1α、αi3及αi5表示。根据式(8)的描述,可以计算得出有效磁通的值。

其中,δk=arcsin(sinδ10cosαLK/cosαL10),αLK=arctan(kω LL/RL),δ10的物理意义如图1所示。根据前文的假设条件,输入电压和电流均为额定频率,该条件下感应式电能表的相位图如图2所示。
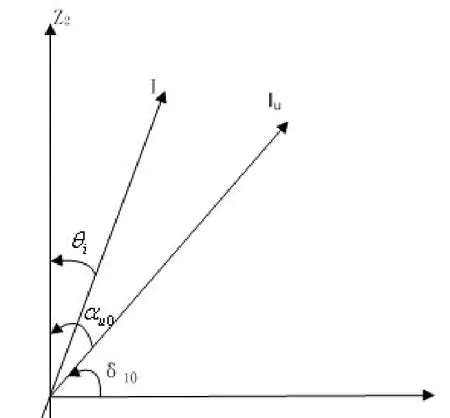
图2 额定功率下感应式电能表相位图
对模型设计过程中谐波影响的电能表误差修正公式为
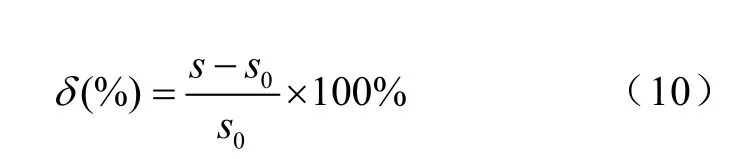
式中,S0是指其他条件(Um、Im、θi)均相同,但是处于额定频率下的电能表指针转速。当计算的 δ为正值时,表示此电能表的指示值偏大,负值则代表测量值偏小。
仿真试验:对该模型进行仿真分析,我们可以通过精密测试电源逐个模拟输出含有不同谐波频率的奇数次谐波的电压和电流,我们在此取3次谐波、5次谐波、7次谐波进行分析,利用智能电能表校验仪测出在这些谐波影响下的电能表计量误差。试验时我们设定基波电压、基波电流含量均为100%。采用该模型与不采用模型的分析结果分别如表1、表2所示,其中10%和30%表示以基波含量为基准时其谐波所占含量。

表1 改造后模型分析结果
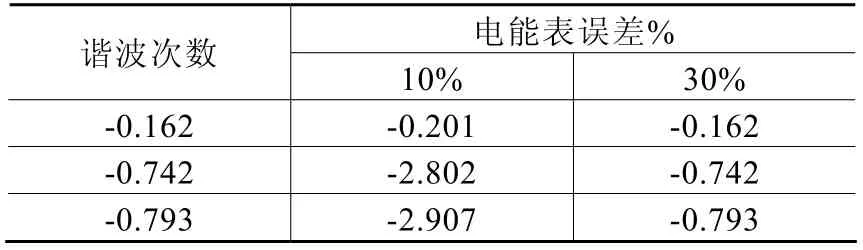
表2 未改造模型的分析结果
由仿真分析可得,采用该模型后和没采用该模型的分析结果有很大的差异,该模型能减少谐波对电能质量的影响,具有一定的发展空间,目前在一些变电站中已得到了一定的应用。
4 结论
从目前对电能表使用情况来看,结合上文分析的结果,高次谐波的大小、方向以及相角均会对其感应式电能表的误差产生不同程度的影响。并且由于电力谐波的存在,常常造成电能表的测量值失准的情况出现。随着测量技术的不断发展,电子式电能表开始在电力系统中得到应用[6]。通过目前应用的经验来看,电力谐波对电子式电能表的计量影响较小,基本可忽略不计。但该经验大多建立在基于全能量计量标准上的。
加强对电能计量的管理,一方面要尽量从技术上对谐波进行合理治理,并最终降低谐波源对电力系统及电力用户的危害,另一方面建议合理采用新的计量方式及标准,形成表差互补,以实现电能的精确计量。
[1]陈建业等.工业企业电能质量控制[M],机械工业出版社,2007.11.
[2]肖雁鸣,毛筱等.电力系统谐波测量方法综述[J],电网技术,2002(6).
[3]B. P Lathi. 线性系统与信号(第 2版)[M].西安∶西安交通大学出版社,2006.4.
[4]李正军.计算机测控系统设计与应用[M].北京∶机械工业出版社,2004.1.
[5]应启珩,冯一云,窦维蓓. 离散时间信号分析和处理[M].北京∶清华大学出版社,2001.9.
[6]许克明,徐云,刘付平.电力系统高次谐波[M].重庆∶重庆大学出版社,1991.9.
