基于模糊控制的光伏系统MPPT

陈广华 杨海柱

（河南理工大学电气工程与自动化学院，河南 焦作 454003）

1 引言

光伏发电具有无污染、无噪声、取之不尽用之不竭等优点，越来越受到关注，在未来的供电系统中将占有重要的地位。制约光伏系统发展的主要因素是初期投资费用和能量转换效率。解决这些问题必须提高光伏阵列的光电转换效率和使其输出功率最大化。

2 太阳能电池阵列特性

（1）太阳能电池的等效电路（见图1）。

（2）太阳能电池是一种光电转换的半导体装置，其产生的电压和电流分别受温度和光照强度的影响。当受光照射的太阳能电池接上负载时，光生电流流经负载，并在负载两端建立起端电压。这时太阳能电池的工作情况可用图1所示的等效电路来描述。

图1 太阳能电池等效电路

（3）太阳能电池的输出功率

当流进负载R0的电流为I0，负载的端电压为V0时，由太阳能电池的等效电路图可以得到如下的解

析式

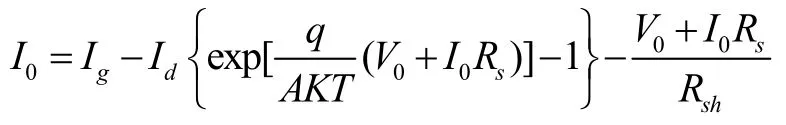
式中，Ig为光生电流；Id为二极管饱和电流；q为电荷电量（l×10-19库仑）；A为二极管因子；K为波尔兹曼常数（1.38×10-23焦耳/度）；T 为开氏温度（K）；V0为电池的输出电压；I0为电池的输出电流；Rs为等效串联电阻；Rsh为等效并联电阻。

且有输出端电压：V0=I0R0

可得太阳能电池的输出功率

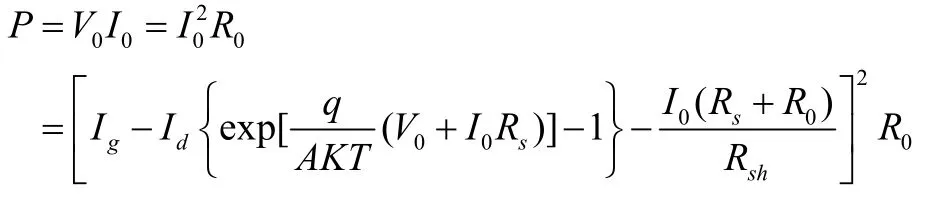
当负载R0从0变化到无穷大时，即可画出如图2所示的太阳能电池负载特性曲线。

图2 太阳能电池的输出特性

由上式和等效电路可知日照强度和电池结温是影响太阳能电池阵列功率输出的最重要参数，图 3表示出了太阳能电池的温度特性，如图所示太阳能电池的开路电压随温度的升高而下降，短路电流随温度的升高而升高，电池的输出功率总的来看随温度的升高而下降。

图3 太阳能电池的温度特性

3 MPPT原理和控制算法

（1）MPPT原理

MPPT实质上是一个寻优过程，通过实时检测光伏系统的输出电压和电流来确定当前工作点与最大功率点的位置关系，然后控制电压向最大功率点对应的电压Vm靠近，直到到达峰值功率点为止。如果电压继续向原来方向变化会引起功率下降，则向反方向调整，最后可控制电压在最大功率点附近一定范围内来回摆动。

（2）MPPT控制算法

常用的最大功率跟踪控制算法有恒电压跟踪算法（CVT）、干扰观察法（P&O）、增量电导法（IC）等。

CVT方式具有控制简单、可靠性高、稳定性好、易于实现等优点，但是光伏阵列最大功率点对应的电压会随环境温度的变化而变化，对于四季温差和日温差环境较大的地区，该方法不能实时跟踪光伏阵列的最大功率点。干扰观察法（P&O）的原理是每隔一定时间增加或减少光伏阵列输出电压，并观测之后其输出功率变化方向，来决定下一步的控制信号。该方法虽然算法简单且易于硬件实现，但相应速度较慢，跟踪步长的设定无法兼顾跟踪精度和相应速度，在特定情况下还会出现误判，只适用于日照强度变化缓慢的场合。增量电导法（IC）是通过比较输出电导的变化量和瞬时电导值的大小来决定参考电压的变化方向。dI/dV＞-I/V参考电压向着增大的方向变化，dI/dV＜-I/V参考电压向着减小的方向变化，dI/dV=-I/V参考电压保持不变。该方法能够适应日照强度的快速变化，控制精度高，dI/dV量值很小，对传感器的精度要求很高，实现起来相对困难。

4 模糊控制的基本原理

（1）模糊控制器的输入量和输出量

根据干扰观察法（P&O）的基本原理，取系统的目标函数为输出功率，控制变量为占空比 D。根据功率值的变化量和前一时刻的占空比来决定此刻的调整步长大小。模糊控制器第n时刻的输入量为光伏系统第n时刻功率值的变化量和第n-1时刻占空比的步长，第n时刻的输出量为第n时刻的占空比步长。

（2）确定输入量和输出量的模糊子集和论域

将功率变化量 ep(n)和占空比步长 ed(n)分别用量化因子量化，然后映像到模糊集合论域Ed和Ep。Ed和Ep分别定义为8个和6个模糊子集。

Ep={NB，NM，NS，NO，PO，PS，PM，PB}

Ed={NB，NM，NS，PS，PM，PB}

其中，NB，NM，NS，NO，PO，PS，PM，PB分别表示的模糊概念为：负大，负中，负小，负零，正零，正小，正中，正大。模糊集合论域离散的数字集合表示为

Ep={-6,-5,-4,-3,-2,-1,-0,+0，1，2，3，4，5，6}

Ed={-6,-5,-4,-3,-2,-1,0,1，2，3，4，5，6}

（3）隶属度函数

根据光伏发电系统特点，选择三角形作为隶属度函数的形状，曲线距离远点越近越陡，便于提高分辨率，距离原点越远越缓，便于提高跟踪速度。功率差Ep和占空比步长Ed的隶属度函数分别如图4，如图5所示。

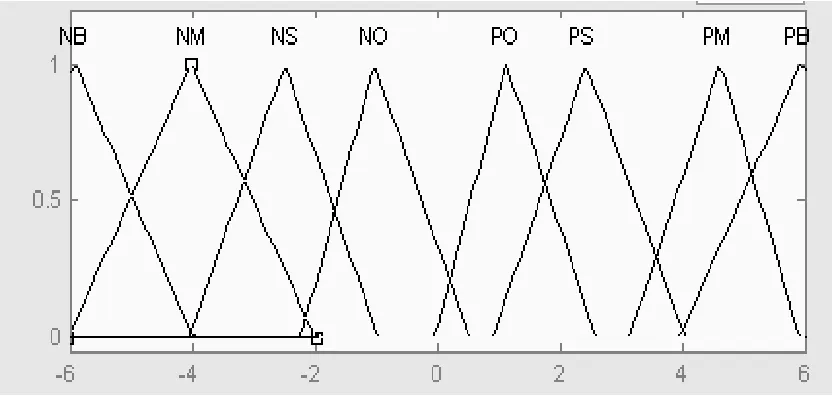
图4 功率误差隶属度函数

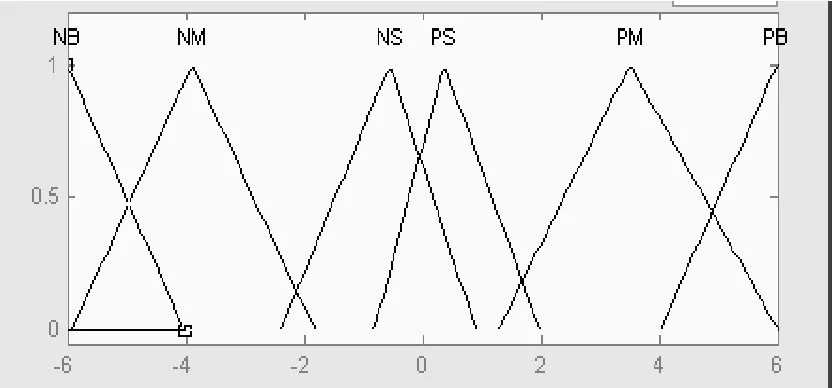
图5 占空比步长隶属度函数

（4）模糊决策表

根据光伏系统输出功率P和占空比D之间的关系，可以得到以下原则：

1）最大功率点较远处，采用较大步长，以加快跟踪速度；最大功率点附近，采用较小步长，以减少搜索损失。

2）如果输出功率增加，则继续向原扰动方向调整，否则向相反方向调整。

3）温度、日照强度等因素发生变化导致功率发生较大变化时，系统能迅速作出反应。

有上述原则，可以得到模糊控制规则表（表 1所示），由 Matlab得到模糊控制规则视图（如图 6所示）。

表1 模糊控制规则表

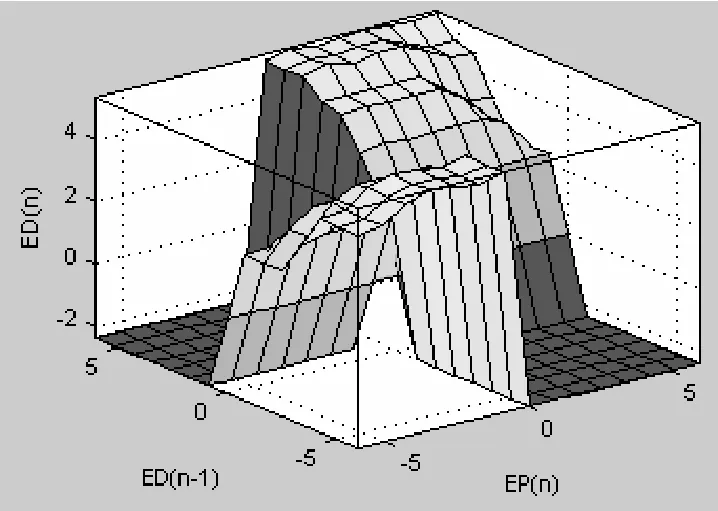
图6 模糊控制规则视图

5 仿真实验

（1）光伏阵列仿真模型

根据光伏阵列数学模型，通过Matlab/Simulink建立太阳能电池模型（如图7所示）。

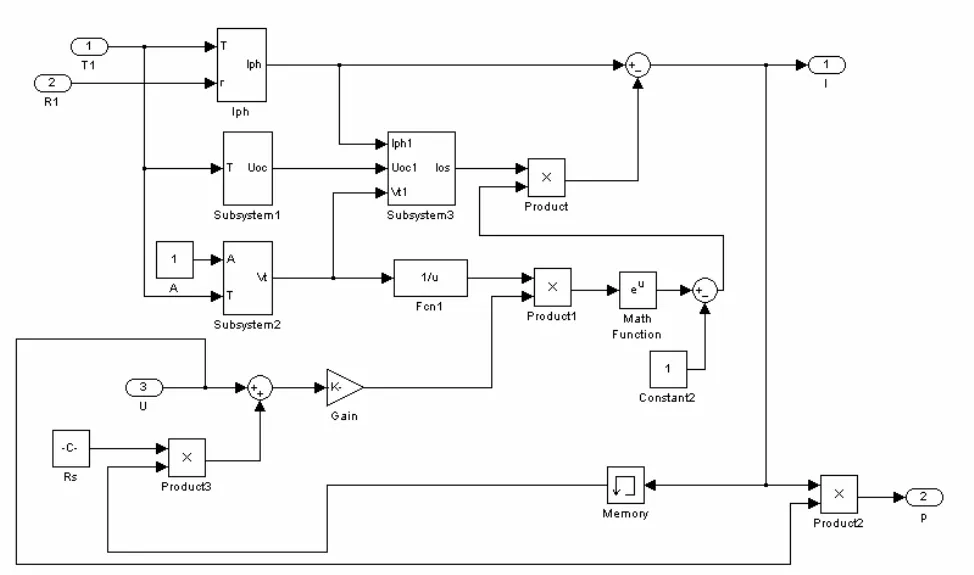
图7 光伏阵列仿真模型

仿真结果择其例如图8～9所示，从中可以看出该模型能较好地模拟太阳能电池的特性。

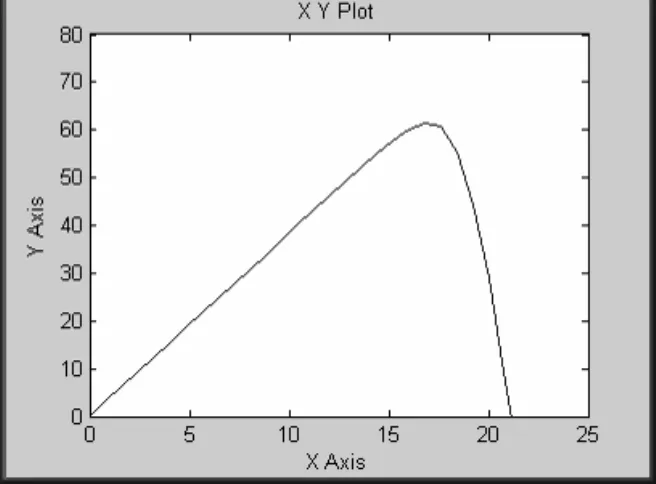
图8 T=25℃，R=800W/m2参数下的P-V曲线

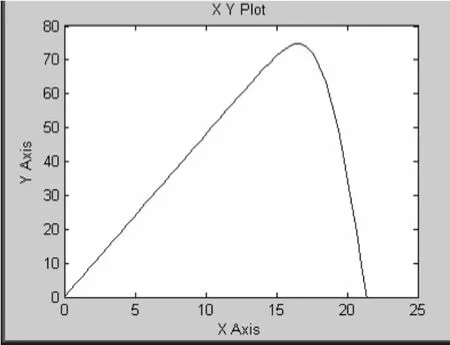
图9 T=25℃,R=1000W/m2参数下的P-V曲线

（2）模糊控制仿真模型（如图7所示）

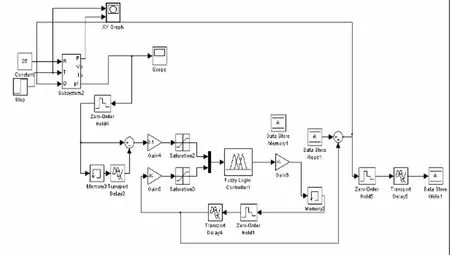
图10 模糊控制仿真模型

（3）仿真结果

光伏电池参数为：表面温度25℃，经反复试验，量化因子分别取0.01，0.1，采用ode23tb算法，仿真时间10s。光伏系统的仿真结果如图8和图9所示。

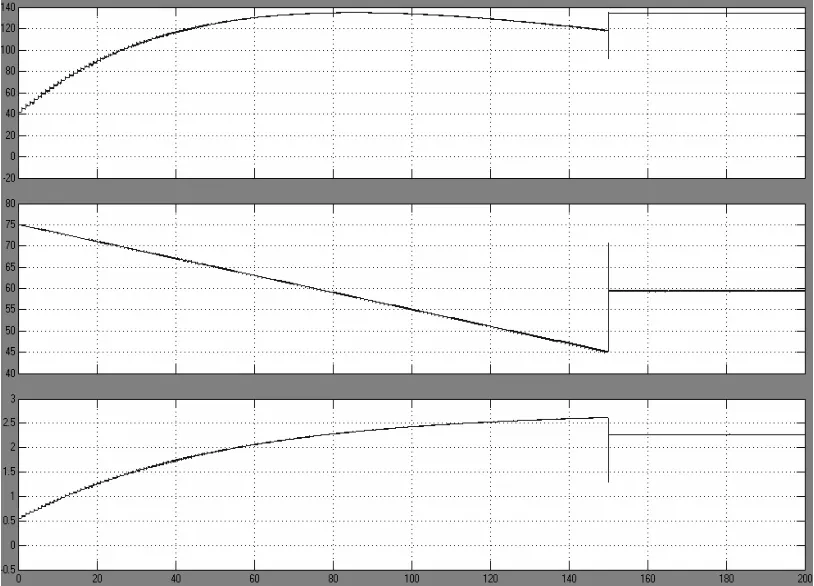
图11 电池阵列输出功率、电压和电流变化过程(P&O)

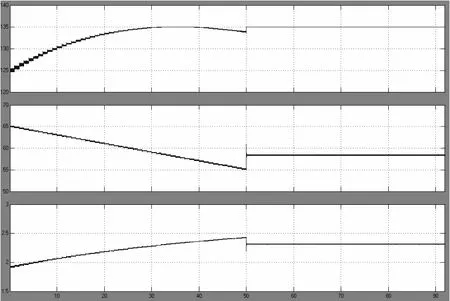
图12 电池阵列输出功率、电压和电流变化过程（模糊控制）

图11和图12分别是采用传统的扰动观察法和采用模糊控制过程中太阳能电池阵列的输出电压、输出电流以及输出功率的变化过程。其中最上面的是功率变化曲线，在仿真过程中太阳能电池阵列的输出功率从0W增加到最大功率135W然后又降到118W，输出电压从75V变化到45V，电流从0.5A变化到2.6A，然后通过 MPPT算法使系统工作在当前的最佳工作点。仿真结果系统的最大功率输出为135W，其对应的开关管占空比值为0.708，此时的太阳能电池阵列的输出电压和电流分别为59V和2.3A。图10的跟踪功率变化速度明显比图9快，即能更快速跟踪光强变化，电压电流的波动也有明显的减小。

6 结论

本文针对光伏电池的非线性和对环境温度、日照的敏感特点，将模糊控制应用到设计的光伏系统最大功率点的跟踪控制中。将占空比步长作为控制变量，根据输出功率变化幅度对占空比进行自适应调节。仿真结果表明，采用模糊控制的光伏发电系统能高效快速跟踪光伏阵列的最大功率点。

[1]沈辉, 曾祖勤.太阳能光伏发电技术[M].北京∶化学工业出版社,2005.

[2]Simoes M G, Franceschetti N N, Friedhofer M.Fuzzy logic based photovoltaic peak power tracking control[A].Proc IEEE Conf.International Symposium on Industrial Electronics [C], Pretoria, 1998, 300-305.

[3]Tomita T, Toward giga-watt. Production of silicon phtovoltaic cells, moduels and systems[A]. Photovoltaic Specialists Conference,2005[C]. Conference Record of the 31stIEEE.NJ. USA∶ IEEE,2005∶7-11.

[4]张超, 何湘宁.非对称模糊PID控制在光伏MPPT中的应用[J].电工技术学报,2005,20(10)∶72-75.

[5]Weidong Xiao, DUNFORD W G. A modiied adaptive hill climbing MPPT method for photovoltaic systems[A]. 35thannual IEEE power electroinc Specialists Conference[C]. Germany,2004,1957-1963.

[6]茆美芹, 余世杰,苏建徽.带有MPPT功能的光伏阵列Matlab通用仿真模型[J].系统仿真学报,2005,17(5)∶1248-1251.

[7]Tafticht. T, Agbossou. K, Development of a MPPT method for photovoltaic systems[A].Electrical and Computer Engineering, 2004 Canadian Conference[C].Canada, 2004,5(2)∶1123-1126.

[8]叶秋香. 光伏电池最大功率跟踪器的模糊控制以其应用研究[D]. 上海∶东华大学,2006.