整流级无零矢量TSMC的研究

董锋斌 皇金锋 蒋 军

（陕西理工学院电气工程系，陕西 汉中 723003）

1 引言

相对于别的电力变换器，矩阵变换器（Matrix Converter，简称 MC）具有以下优点：①输入电流可控制成正弦，对电网谐波污染很少；②输入功率因数任意可调；③能量可双向流动，具有四象限运行的功能；④无中间直流储能元件，变换器体积小，效率高。MC自提出来至今已有三十多年的发展，虽取得了许多成果，但至今仍停留在理论研究和实验样机阶段，不能广泛使用，主要原因有：①复杂的四步换流增加了控制的难度，降低了系统的可靠性；②控制策略复杂；③钳位电路开关数量多，系统成本高等[1]。作为MC家族中的双级矩阵变换器（Two stage Matrix Converter, 简称TSMC）具有以下特点：①无需采用MC的四步换流法，整流级开关可实现零电流换流，逆变器开关采用传统的逆变器换流方法，提高系统的可靠性；②具有和MC一样的输入输出性能；③利用中间直流环节作为母线，可实现多逆变器输出；④在一定约束条件下，可以减少开关器件的数量。因此，TSMC是一种更具有发展潜力的新一代绿色环保型电力变换器[2-3]。对其进行研究，将有助于TSMC产品化和广泛使用。

2 TSMC的基本原理

2.1 TSMC的拓扑结构

如图1所示，TSMC的拓扑结构如图1（a）所示。在图 1（a）中， Skj表示理想双向开关，k ∈ {a, b, c, A, B, C}， j ∈{ p , n}。TSMC能量要能双向传输， Skj均采用双向功率开关，若由两个单向功率开关组合成一个双向开关，TSMC拓扑中需要24个单向开关。在有些工况下，不需要能量双向传输，TSMC的拓扑中仅需要9个单向开关。但最常用的是 18开关的 TSMC，如图 1（b）所示。为了获得最大的电压利用率，整流级无矢量的TSMC被认为是较好的一种调制策略[4]，这里就此为研究对象，对其原理进行分析。

2.2 TSMC的调制策略

TSMC中将整流级和逆变级分开，下面分别讨论整流级调制和逆变级调制。

（1）整流级的调制

图1 双级矩阵变换器的拓扑结构

双向开关整流级的调制目的主要有两点，其一是要在直流侧输出为正的直流电压，并获得最大的电压利用率。其二是使输入电流矢量跟随输入电压矢量按正弦规律变化，以保证单位输入功率因数[5]。

设TSMC三相输入相电压为

式中，Uim为输入相电压的幅值，ωi为输入角频率。θa、θb、θc为三相输入电压的角度。

为实现目的一，将输入相电压的周期分为六个区间，每个区间的特点是：一相电压绝对值最大，另外两相极性相反，如图2所示。将每个PWM调制周期分为两段，分别在两段时间内将相应的两个最大且极性为正的线电压由直流侧输出。以第一区间为例， ua绝对值最大， ub， uc极性与 ua相反，两

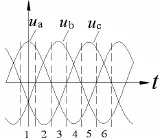
图2 输入电压6区间的划分

个线电压分别为 uab、 uac，那么在一个PWM周期内的第一段，控制相应开关使 upn= udc= uab，在第二阶段，使 udc= uac。其余五个区间依次类推。

为实现目的二，应使每相输入电流的大小在任意时刻与其同一相电压成正比关系。即在一个PWM周期内，应该保证各相输入电流局部平均值与相应输入电压值成正比。以第一区间为例，在一个PWM周期内，局部直流平均电流为一恒定值，三相输入电流局部平均值为输出直流电压 uab、对应的两个时间段的占空比分别为 dab、 dac。若三相电压平衡时， dab+ dac= 1 。

实现目的二有下式成立

式中， ka、 kb、 kc分别为各相电压与电流的比例系数。

将式（3）代入式（2）得到

将式（1）代入式（4），并根据三相对称性，得到

式（5）对任意的θb、θc均成立。

将式（6）代入式（2）得到

整流级在第一区间内一个 PWM周期内的直流平均电压为

其他区间在一个 PWM周期内两个时间段的开关状态，占空比和对应的直流电压为表1。

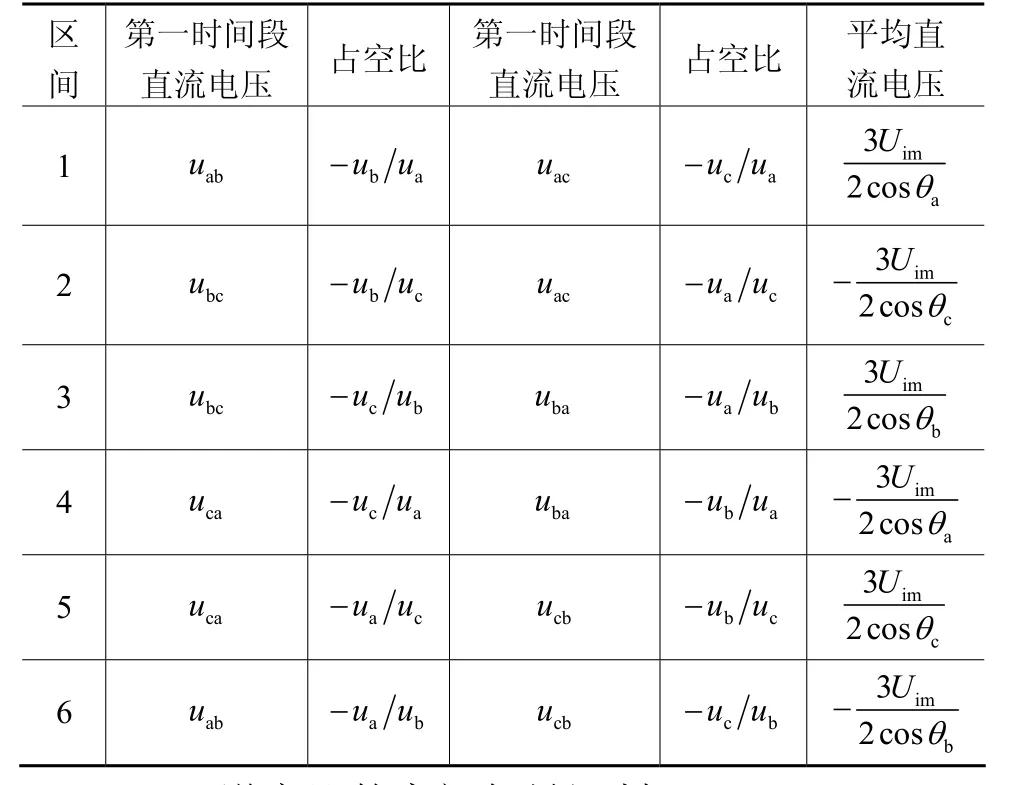
表1 6个区间的一个PWM周期内的对应的直流电压、占空比和平均的直流电压

（2）逆变器的空间矢量调制

采用常规DC-AC逆变器可靠的换流方法，调制可采用SVM方法，不同的是常规DC-AC逆变器直流电压为恒定值，而TSMC的逆变级在一个 PWM周期内的直流电压为不等的两级直流电压。当假定直流电压 udc=U恒定值时，其SVM调制的示意图如图3所示。

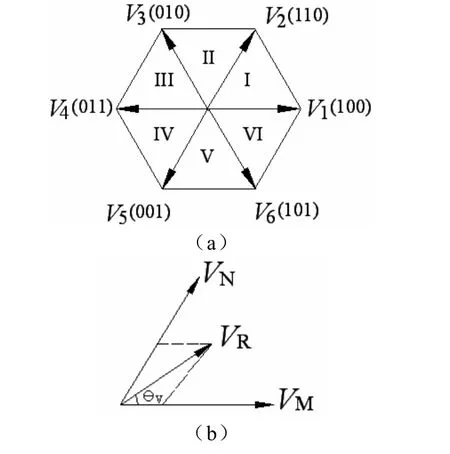
图3 逆变级SVM调制

根据空间矢量调制原理， VR落在六边形空间矢量中的某个区间内，其相邻两有效空间矢量为 VM、VN， VR由矢量 VM和 VN合成， V0为零矢量。有

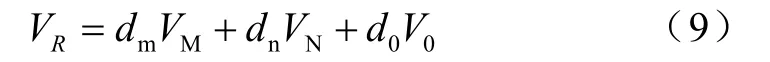
VM、 VN、 V0占空比分别为

式中的m为逆变级调制系数，有

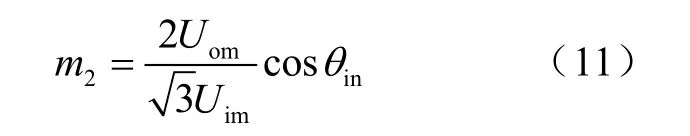
式中， Uom为输出相电压的幅值，

其中， c osθin部分用来与直流平均电压中的波动量相抵消，以保证输出电压幅值恒定。

（3）开关矢量顺序

整流级电路在两个时间段给逆变级提供不同的直流电压，因此逆变级调制在两时间段内分别进行。两个时间段的直流电压，开关矢量顺序图为图4（a）、（b），为保证整流开关的零电流换流，一个 PWM周期内整流级和逆变级开关的切换控制如同 4(c)所示。其中 Ts为PWM周期。在 tab时间段内， VM矢量作用的时间为 tMab，VN矢量作用的时间为 tNab，Vo矢量作用的时间为 t0ab；在 tac时间段内， VM矢量作用的时间为 tMac，VN矢量作用的时间为 tNac，Vo矢量作用的时间为 t0ac。

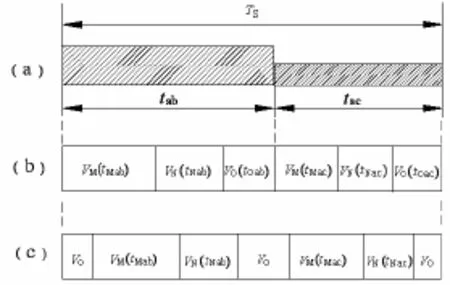
图4 开关矢量顺序

3 仿真验证

根据以上原理，采用 PSIM软件对调制策略进行验证。仿真参数：输入三相对称电源为380V/50Hz；输入侧滤波电感为 Li= 0 .5mH ，滤波电容 Ci= 15μF ；输出侧滤波电感为 Lo= 0 .6mH，滤波电容 Co= 17μF；负载为三相对称阻感负载，每相电阻为4Ω，电感为1mH；Ts= 0 .1ms ；输出频率为100 Hz。仿真结果如图5，其中图5（a）输入侧未加滤波电感、电容时的直流电压波形；图5（b）为输入侧加滤波电感、电容时的直流电压波形；图5（c）为输入侧的a相电压、电流波形；图5（d）为三相输出相电压波形。

从仿真波形来看，直流电压为脉动的直流波形，跟理论分析一致；输入侧电压与电流同相位，可实现单位功率因数；输出三相相电压波形呈正弦规律变化，符合负载要求。

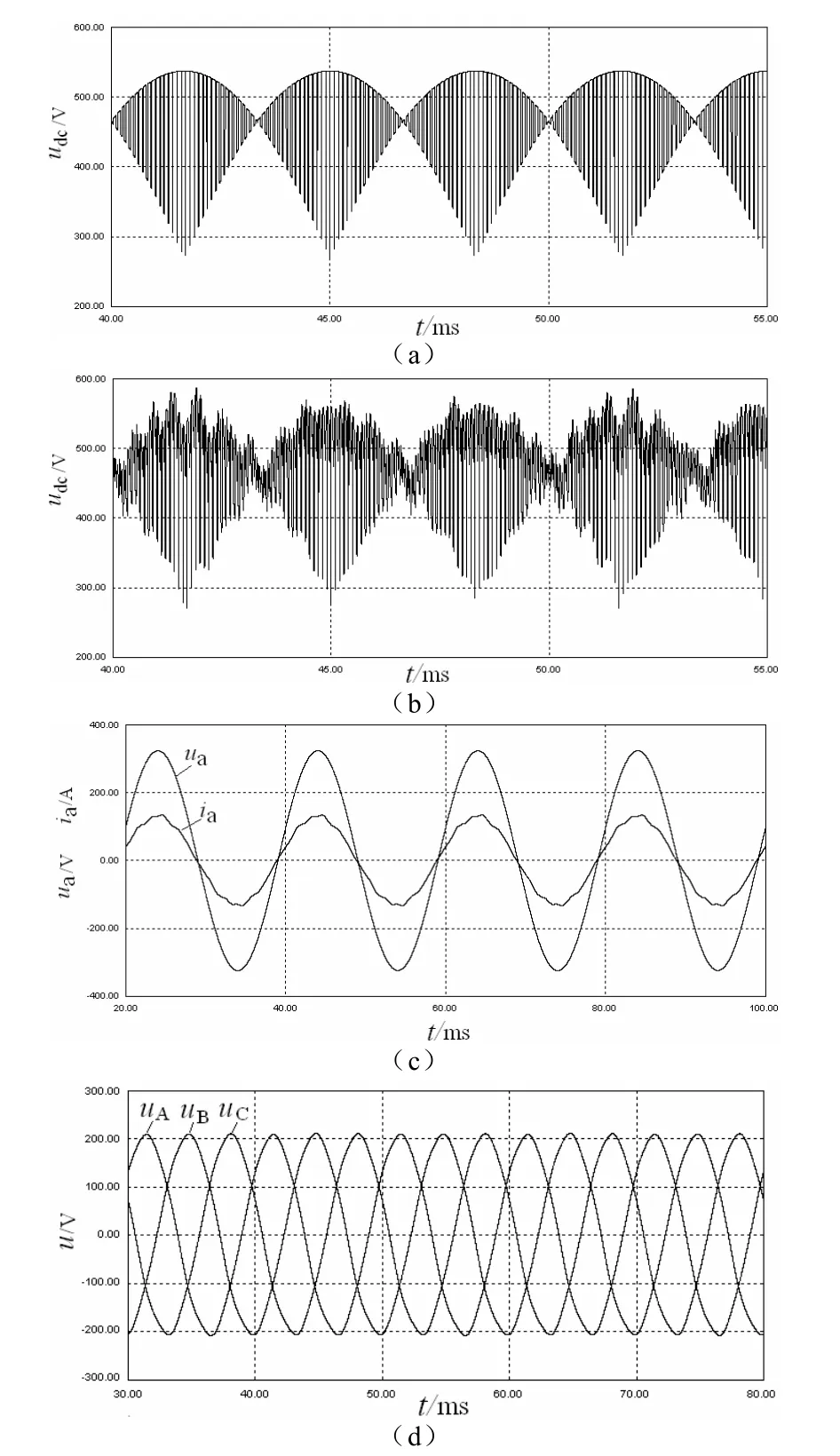
图5 仿真实验波形

4 结论

本文讨论了双级式矩阵变换器整流级和逆变级的工作原理和调制策略。依据双向开关整流级无零矢量的调制目的，推导了整流级调制占空比的数学表达式。利用PSIM仿真软件对TSMC的调制策略进行验证，仿真波形表明了理论分析的正确性，为TSMC的物理实现将起到一定的推动作用。

[1]孙凯,周大宁,梅杨. 矩阵式变换器技术及其应用[M].北京:机械工业出版社,2007.

[2]Klumpener C, Blaabjerg F. Modulation method for a multiple driver system based on a two-stage direct power conversion topology with reduced input current ripple[J]. IEEE Transactions on Power Electronics, 2005,20(4): 922-929.

[3]Klumpener C, Wheeler P. Blaabjerg F. Control of a two-stage direct power converter with single voltage sensor mounted in the intermediary circuit [C]//Proceedings IEEE PESC2004 ,2004,3:2386-2392.

[4]邓文浪,杨欣荣,朱建林,等. 18开关双极式矩阵变换器的空间矢量调制策略及其仿真研究[J]. 中国电机工程学报,2005,25(15):84-90.

[5]邓文浪. 双极式矩阵变换器及其控制策略研究[D].长沙:中南大学博士学位论文,2007.