基于几何参数化的连续潮流算法研究

向 洁 韩富春 李少华 杨 宇

（1.太原理工大学电力与动力学院，太原 030024；2.山西省电力公司，太原 030001）

1 引言

在电力系统电压稳定性研究中，PV曲线是进行电压稳定研究的有效工具。PV曲线的求取可以获得电力系统电压稳定的功率传输极限和电压稳定的临界值[1]，因此PV曲线的准确求取对电力系统静态安全及电压稳定具有重要意义。

采用常规潮流计算方法求取 PV曲线，在负荷接近临界点时，往往会出现雅克比矩阵奇异，导致迭代不收敛[2]。针对在鞍结分岔点附近的潮流迭代不收敛的问题，近年来，众多研究人员提出了各种计算传输功率极限的方法和各种不同的解决方案。如文献[3]对重负荷节点采用导纳模型；文献[4]通过回避崩溃支路来进行不含崩溃支路的潮流迭代；文献[5]中引入参变量参数化，避开雅克比矩阵的奇异；文献[6]中提出利用潮流多解，采用新的变量形成雅克比矩阵。以上这些方法对电压稳定极限的求取已经取得了一系列的研究成果

本文在基于连续潮流法算法基础上，提出了一种改进的连续潮流算法。该算法采用几何参数化，通过增加一维校正方程改变雅可比矩阵结构。从而改变其收敛方向，有效地消除了在分歧点附近的雅可比矩阵奇异的现象，避免了在极限传输点的迭代发散。可以精确获得电压稳定极限以及完整的 PV曲线。

2 算法原理

2.1 连续潮流的基本原理

电力系统的常规潮流方程可以表示如下，记为

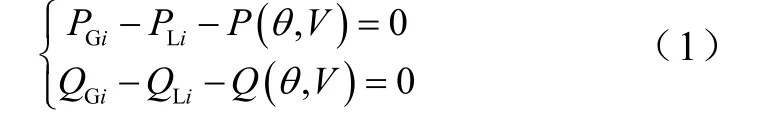
其中，式（1）中的PGi，QGi分别表示第i个节点的发电机出力，PLi，QLi表示第i个节点的负荷，V和θ分别表示电压的模值和相角。

若在式（1）中加入未知量λ，表示发电机和负荷的增长；Kpg，Kpl，Kql分别表示发电机和负荷的有功、无功增长的方向向量。此时形成以负荷变化为参数的潮流方程可以表示为如下

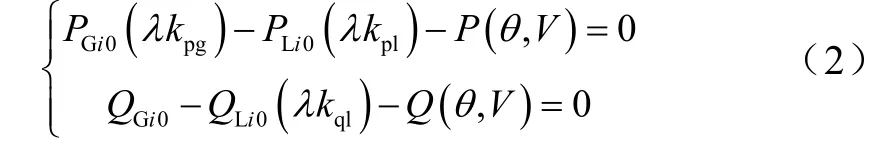
在（2）式中，当λ=1时，PLi0，QLi0，PGi0分别表示初始条件下PQ节点的有功、无功以及PV节点的有功，因此它既适用于单个的节点也适用于整个系统。一旦负荷变化方式和发电机模型确定了，就可以采用常规潮流法计算出各种负荷条件下的电压值。

若用矩阵和向量表示潮流[7]。则可以表示为

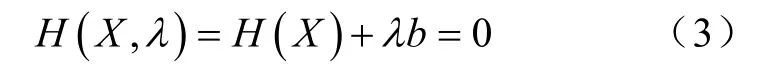
潮流方程的状态变量X表示V和θ。为了求取潮流的下一步解，先采用切线预估来近似估计下一步的状态变量的解。将式（3）求取全微分，在 X0处展开

由于潮流方程中引入参数λ，增加一个未知的状态变量，因此需要增加关于λ的一维规范化方程，从而使潮流雅可比矩阵相应的增加一行和一列。扩展后的潮流方程[8]可以表示为

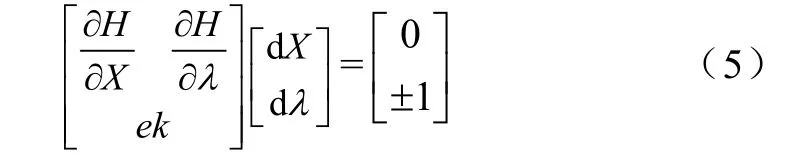
在式（5）中，ek是行向量，除了第k个元素为1以外，其他的元素均为0。由方程组可得到切向量，再确定步长因子为σ，下一步的预报解为

然后，预测下一个运行点，迭代求解得到真解。以上即为连续潮流法的基本原理。

2.2 连续潮流法所存在的问题

目前连续潮流法存在的主要问题如下：

（1）局部参数连续法：该方法通过控制连续变量对曲线进行参数化。在修正方程中新增方程是将某一个连续变量值固定，这个连续变量可以是节点的电压幅值V或负荷增长参数λ，其参数化方程表示为

图1 局部参数连续示意图

（2）正交参数法：该方法采用了预测方向的正交面作为实际值的校正路径，其增加的参数方程表示为

其中，式（9）中ΔX，Δλ为每次迭代的预估值，在迭代时为常量。从图中可以看出，在接近临界点时，预估值的正交平面也有可能与 PV曲线没有交点，同样会使得迭代无法收敛[10]。

图2 正交参数法示意图

（3）弧长参数法：该方法虽然这是对正交法的改进，但采用曲线的弧长进行非线性方程的参数化，校正过程为沿着所给定的弧长所确定的圆弧上来追踪实际解，其参数化方程

虽然在N+1维的平面中的超球面或超椭球面可以与曲线相交，可以实现步长随曲线曲率自动变化，但是在电压极限点的附近，会因为曲率过大而弧长半径会绕过临界点，仍然会因与曲线无法相交而没有解[11]。

3 改进算法

针对目前连续潮流在改变收敛方向中所存在的问题：即在改变收敛方向的过程中可能存在不收敛现象。本文提出采用几何原理，重新构造第N+1个方程，所得的方程可以表示为

图3 几何参数法示意图

如图3所示，其中，每一步的预估步为（Vk，λ），而（Vk0，λ0）是在平面选取任意一个固定点，是一个相对独立的变量。α为节点电压与有功功率的正切值，其预估步长与固定点的连线方向就是收敛方向，新的雅可比矩阵为

对于固定点的选取，一般取在所求曲线的电压最大点和最小点之间，使得这个点与曲线上每一个点都有交点，这样就可以保证在校正过程中每一步校正都收敛。一般取其中间值（（Va+Vb）/2，( λa+λb)/2）为固定点。（其中为（λa，Va）为初始值，(λb，Vb)为最后一个值）。

对于每一步校正而言，α是一个可算出的固定常数。α的获得是通过下面的公式[12]

其中，每预估一次，α的值就需计算一次。而在每步的校正过程中，α保持不变，校正步的收敛方向也就确定了，这样就可以绘出完整的 PV曲线了。从理论上，只要固定点选择恰当就不会存在不收敛的问题。而连续参数X的选取，一般选择沿切线方向变化较快的变量。

4 算例分析

本文通过对IEEE39节点和IEEE118节点的电力系统进行计算，并按本文所述的方法编写几何参数化的程序进行计算分析。系统负荷增长方式均为有功和无功等比例同时增长，步长因子σ取0.01～0.02之间，仿真中取容许误差为10-6。

图4 几何参数法的IEEE39节点全网负荷增长时总负荷的PV曲线

对 IEEE39节点的系统采用本算法，选取固定节点（Vk0=0.8，λ0=0），并通过公式（13）计算出参数α。图4是全网负荷同时增长时总负荷的PV曲线。从图中可以看出，几何参数连续潮流法在计算过程中都比较稳定，即使在临界点也保持着良好的收敛性，可一直计算到 PV曲线的下半枝，整个过程的每一步迭代均不超过5次，能够完整的绘出整条PV曲线。

图5 几何参数法的IEEE118节点系统全网负荷增长时单个节点（43与44节点）的PV曲线

对118节点的系统计算可以得到相同的结论。如图5和图7所示，分别表示全网负荷增长时单个节点的 PV曲线（43和 44节点）和系统总负荷的PV曲线，初始点参数设为（0.85，0）。并在相同条件下，并用本算法的计算结果同正交参数法进行了比较。

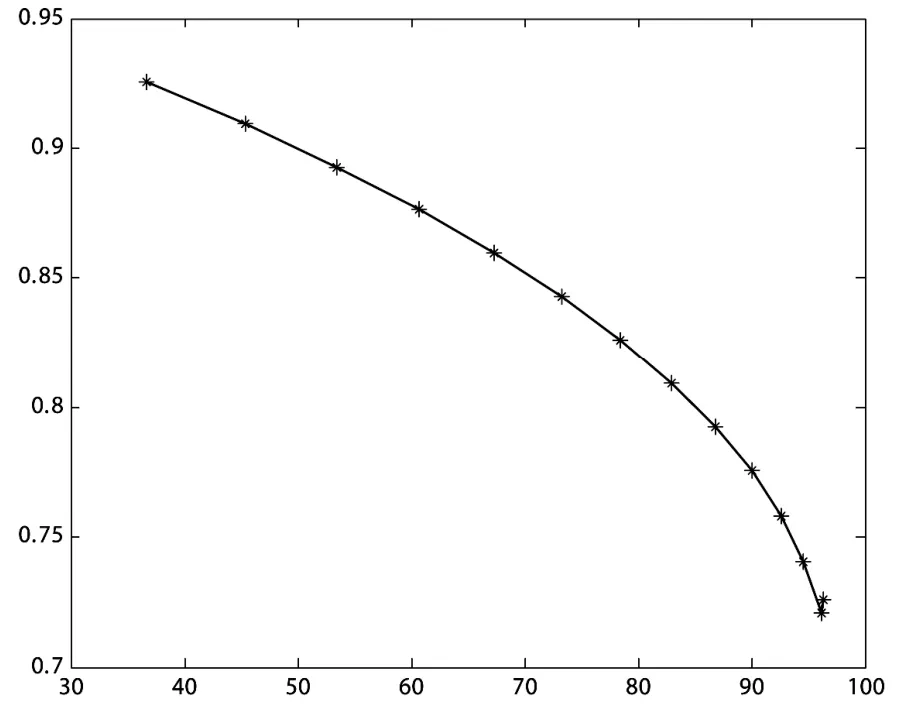
图6 正交参数法的IEEE118节点全网负荷增长时总负荷的PV曲线

图7 几何参数法的IEEE118节点全网负荷增长时总负荷的PV曲线

通过对图6的正交参数法和图7的几何参数法计算结果的比较：图6表明正交法在功率增长还没有到达临界值时就已经出现不收敛的现象，而本算法绘出的 PV曲线在临界点附近没有遇到迭代不收敛的问题，可以一直计算到 PV曲线的下半支，可以完整地绘出整条PV曲线。

5 结论

（1）本文给出了一种求取电力系统PV曲线的改进算法。该算法是以连续潮流为基础，采用了几何参数化，有效地解决了迭代过程中的振荡及不收敛问题，并保持较好的收敛性。可以精确地求出整条PV曲线和功率极限电压的临界值。

（2）本文所提出的算法原理简单，求解的过程稳定，只需对原来连续潮流程序稍作修改即可完成。

[1]周双喜,冯治鸿,杨宁.大型电力系统 PV 曲线的求取[J].电网技术,1996,20(8):4-8.

[2]祝达康,程浩忠.求取电力系统PV曲线的改进连续潮流[J].电网技术,1999,23(4):37-40.

[3]张尧,宋文南.节点电压稳定临界状态和弱节点的确定[J].中国电机工程学报,1993,13(6)：40-45.

[4]杭乃善,廖青华等.电力系统临界电压崩溃潮流的柔性节点算法[J].中国电机工程学报,2005,25(17):57-61.

[5]Chiang H DA more efficient formulation for computation of the maximum loading points in electric power systems[J].IEEE trans on Power Systems, 1995,10(2):623-634.

[6]程浩忠.电力系统电压崩溃临界状态的近似算法[J].电力系统自动化,1996,20(5):14-18.

[7]周双喜,朱凌志,郭锡玖等.电力系统电压稳定性及其控制[M](第一版).北京:中国电力出版社,2004.

[8]江伟,王成山.电力系统输电能力研究中PV曲线的求取[J].电网技术,2001,25(2):9-12.

[9]S-H.Li H-D.Chiang.Nonlinear Predictors and Hybrid Corrector for Fast Continuation Power Flow[J].IET Gener.Distrib.2008,2(3):341-354.

[10]蔡伟程,代静.对求取电力系统PV曲线的连续潮流的改进[J].电力系统及其自动化学报,2005,17(5):82-85.[11]余一平,刘俊勇.基于最优乘子的PV曲线求取方法[J].电力系统自动化,2006,30(2):12-15.

[12]A.Bonini Neto,D.A.Alves.An Efficient Geometric Parametrization Technique for the Continuation Power Flow through the Tangent Predictor[J].TEMA. Tend.Mat.Aol.Comput. 2008,9(2):185-194.