基于车轨耦合振动的弓网接触压力研究
2010-06-22徐海东马峰超
徐海东,许 敏,马峰超
0 引言
弓网接触压力不仅可用来评价接触网的运行质量,而且是接触悬挂及受电弓技术性能的重要评价内容。研究弓网系统动力学,分析弓网接触压力,对于保证铁路安全运营具有十分重要的意义。随着列车运行速度的提高,机车与轨道的耦合振动增强,同时由受电弓底座传至弓网系统的振动干扰也将随之加大。因此,车轨耦合振动对弓网接触压力影响的研究是个很重要的课题。
1 弓网系统动力学线性分析
1.1 弓网系统动力学模型
接触网与受电弓耦合模型如图1所示,受电弓采用二元受电弓。
图1 中,M1、C1、K1、y1、M2、C2、K2、y2分别为受电弓模型中弓头和框架的质量、阻尼、刚度及位移;y3为受电弓底座振动位移;y(x,t)为接触网t时刻的位移;F0为静态抬升力。
1.2 接触线振动微分方程
接触悬挂就整体而言为柔性状态,但从局部看,线索自身都具有一定的刚度。当受电弓以速度V匀速通过接触网时,根据参考文献[1]可得出接触线的动力平衡方程:
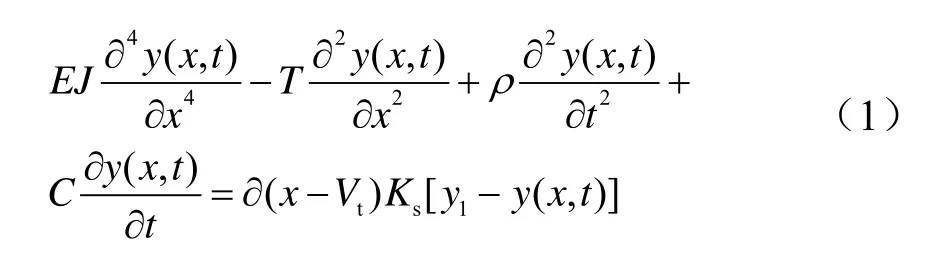
式中,EJ、T、ρ、Ks、C分别为接触线的抗弯强度、张力、线密度、刚度、阻尼系数;Vt为t时刻受电弓的横坐标。
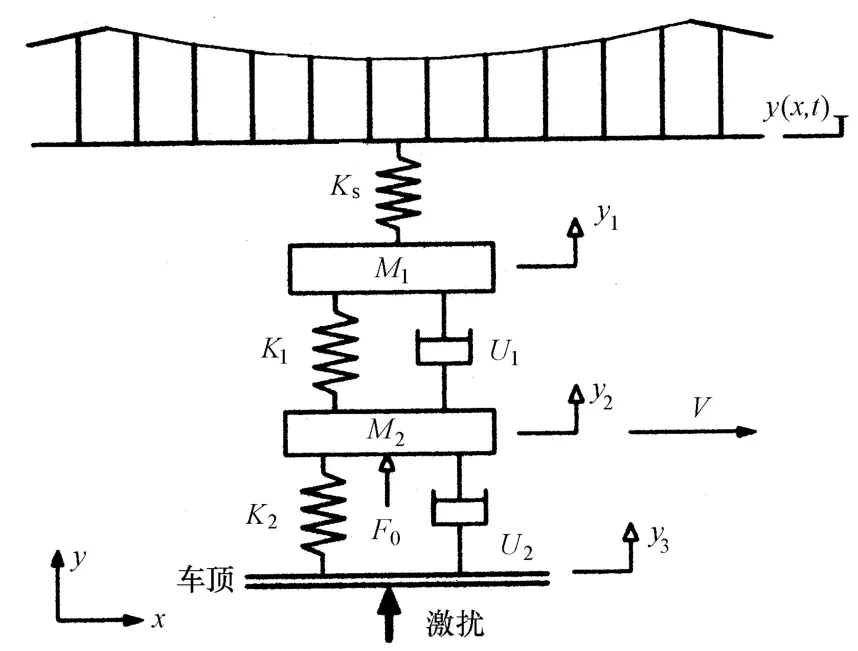
图1 弓网耦合系统动力学模型图
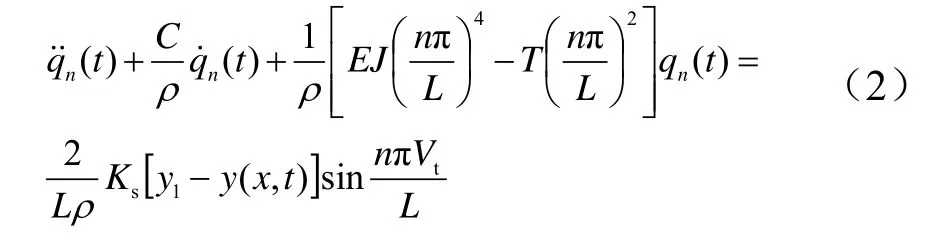
1.3 弓网动力学微分方程
受电弓线性模型的建立,主要是对框架结构的线性化处理。首先假定受电弓的基座固定不动(即不考虑机车振动),得到受电弓运动微分方程[1]:
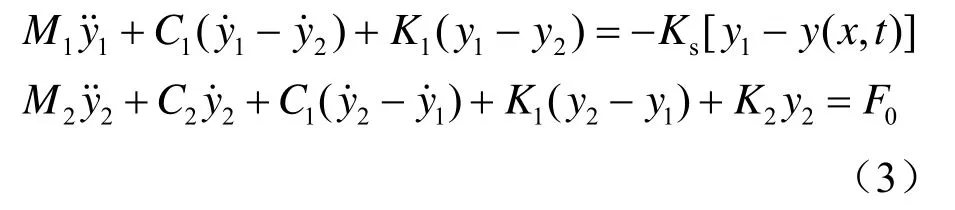
受电弓与接触网系统通过接触压力 FC=Ks[y1- y(x,t)]耦合在一起,联立受电弓、接触网的动力平衡方程,就得到了弓网动力平衡方程组:
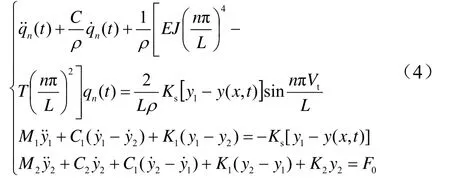
2 弓网系统动力学仿真
利用计算机仿真技术对高速铁路弓网关系进行分析研究是一种行之有效的途径。根据上述弓网系统模型的数值模拟仿真,结果如图2所示。其中,接触网悬挂类型为简单链形悬挂。从仿真结果中可以看出,在每一跨距中接触压力变化基本一致。
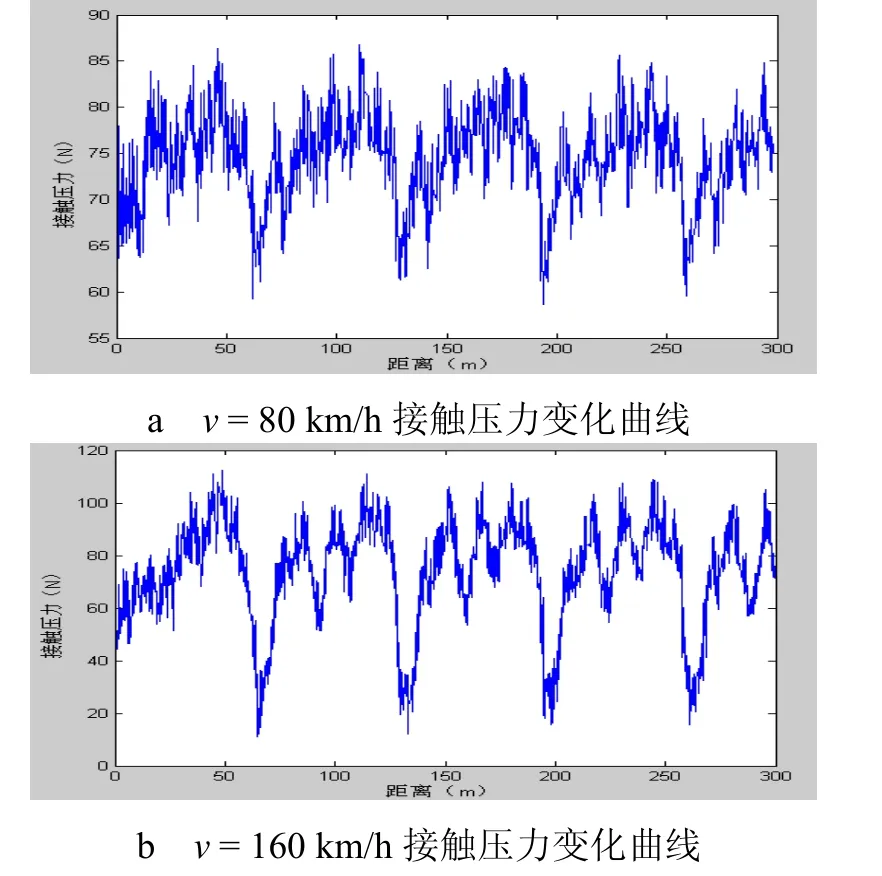
图2 弓网系统模型的数值模拟仿真结果示意图
3 耦合振动下系统动力学分析
具有独立自由度的集中质量,其振动力即等于质量的振动惯性力;按广义坐标离散的简支梁,其振动力为对应各振型的广义振动惯性力。如图1所示,列车振动作用在受电弓弓头和框架上的惯性力为
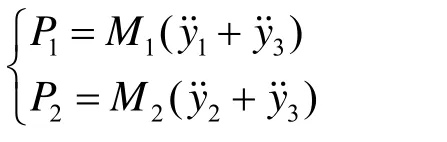
此时受电弓运动微分方程表达式为
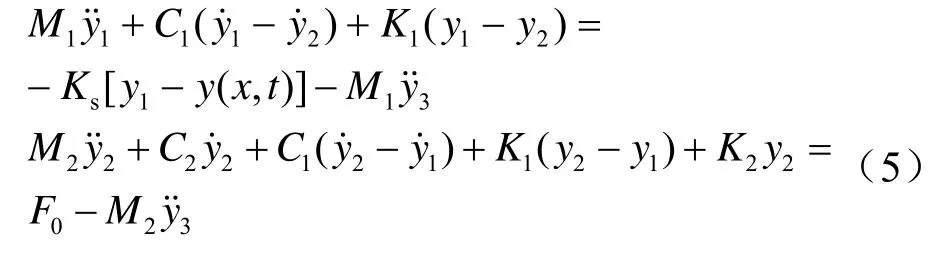
若体系以匀速V在接触线上通过,接触线的动力平衡方程为
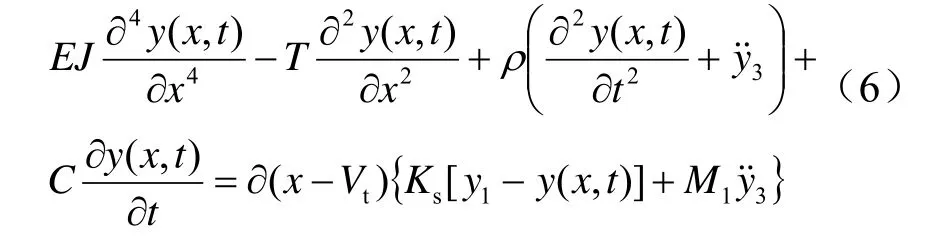
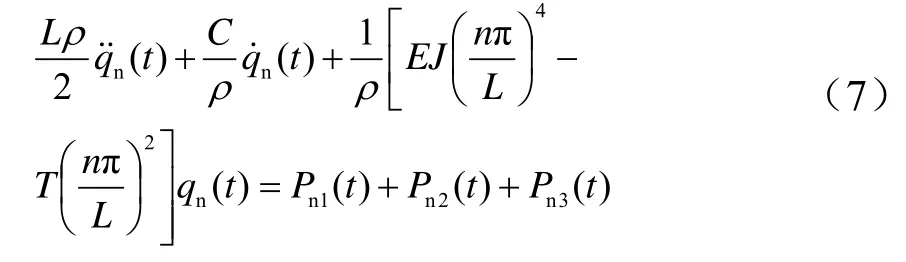
式中,Pn1(t)为没有机车振动时接触网的广义力,Pn2(t)是接触网自身产生的广义力。对于简支梁,只有奇阶振型起作用,偶阶振型的积分为零,即
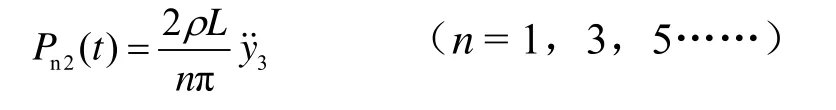
Pn3(t)为受电弓弓头M1对接触网产生的广义力,其表达式为
此时弓网的动力平衡方程组为
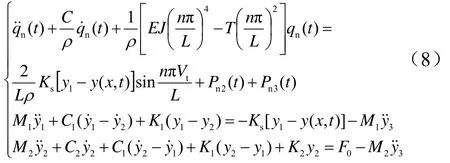
可见弓网系统仍然通过接触压力 Fc耦合在一起,但机车振动载荷部分不参与该种耦合。整个系统运动方程表达式为

式中,Y、F、M、C、K分别为广义位移矩阵、广义力矩阵、广义质量矩阵、阻尼矩阵、广义刚度矩阵。其中F = FA+ FB。式中,FA为无机车振动时的广义分量,FB为机车振动激发的广义分量:
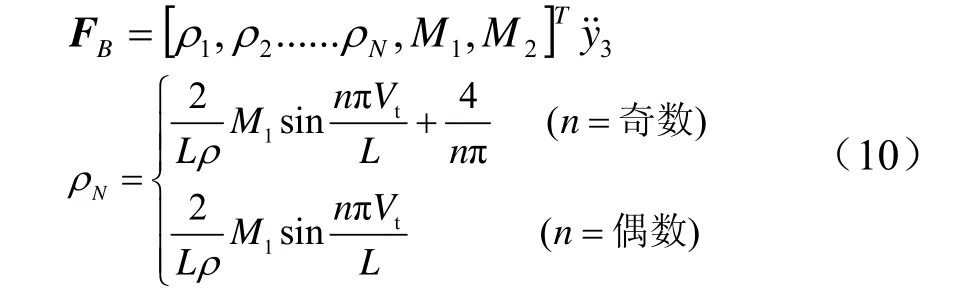
由上述分析可知,受电弓与接触网系统在机车振动的动力作用,在建模时只需在原来的体系运动方程中加上振动力即可。
4 振动对弓网接触压力的影响
4.1 车轨耦合振动的响应
当轨道存在不平顺时,机车与轨道的耦合振动增强。获取机车顶部受电弓底座处的振动响应作为弓网系统的激扰,输入至弓网动力学模型,得到不同速度下受电弓基座振动加速度响应[2],如图3所示。由图可见速度较高时机车振动对弓网系统的激扰比低速运行时要大得多。
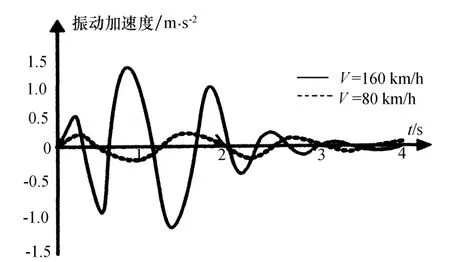
图3 不同速度下受电弓基座振动响应比较图
4.2 车轨耦合振动下弓网动力学仿真
根据弓网系统模型,将机车顶部受电弓底座处的振动响应作为弓网系统的激扰,输入至弓网动力学模型,进行数值模拟仿真计算,结果如图4所示。对比图2可知,机车以80 km/h运行时,弓网接触状态较为稳定,机车振动较弱,因而机车振动对弓网动态相互作用关系的影响也很弱。当机车运行速度提高到160 km/h时,受电弓基座处振动激扰加大机车振动对弓网关系的影响,接触压力波动加剧。
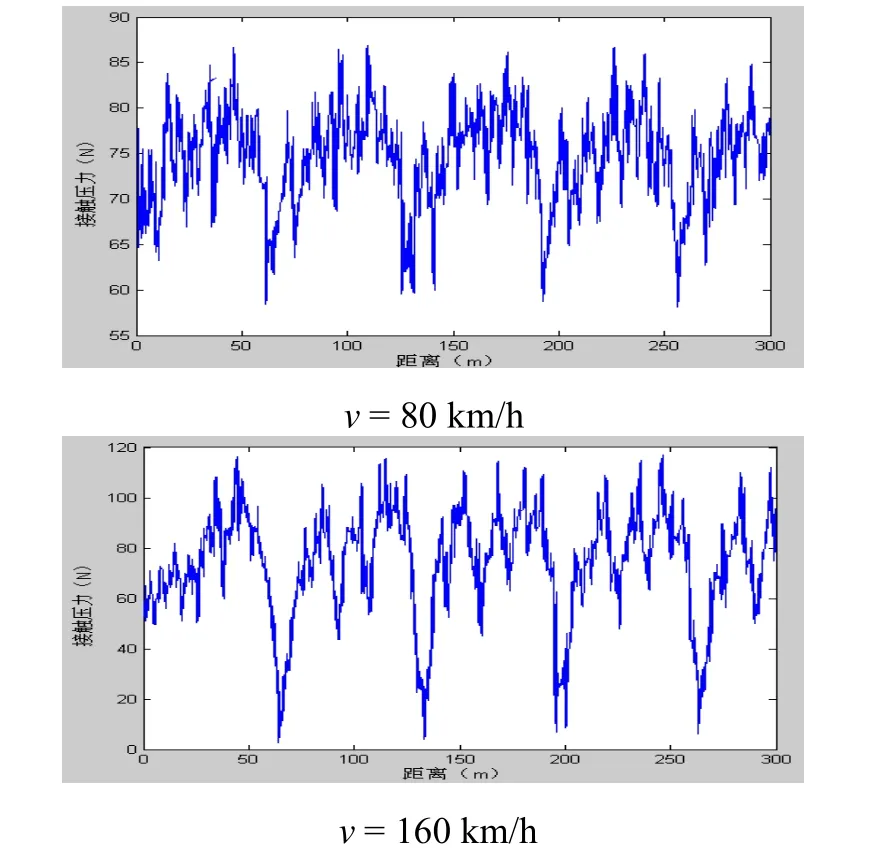
图4 车轨耦合振动下接触压力变化曲线图
5 结束语
通过将机车顶部受电弓基座处的振动响应作为弓网系统的激扰输入,对弓网动力学模型进行分析,从而得出列车在高速运行状态下,车轨耦合振动对弓网接触压力会产生较为显著的影响。因此基于铁路大系统动力学理论,探讨车轨耦合振动对弓网接触压力的作用,具有十分重要的现实意义。
[1]于万聚.高速电气化铁路接触网[M].成都:西南交通大学出版社,2002.
[2]翟婉明.车辆-轨道耦合动力学[M].北京:科学出版社,2007.
[3]付秀通,詹斐生.轮/轨-弓/网系统耦合动力学数值模拟分析与试验研究[J].铁道学报,1998.
