变压器铁芯磁滞回线模型参数辨识
2010-06-21袁中琛刘连光
袁中琛,刘连光
(华北电力大学电气与电子工程学院,北京102206)
变压器铁芯磁滞回线模型参数辨识
袁中琛,刘连光
(华北电力大学电气与电子工程学院,北京102206)
0 引言
硅钢片的磁滞特性对变压器偏磁饱和时运行性能具有很重要的影响,因此,了解和分析磁性材料的磁滞特性具有很重要的意义。磁性材料的磁化包含了不同的磁化过程,如磁畴壁的弯曲和旋转等,其中的机理比较复杂。对磁滞特性的描述有Presiach、Jiles-Atherton(J-A)等模型[1-2]。J-A模型以物理原理为基础,不是实验数据的拟合,这一模型仅包含一个微分方程,并具有参数简单等特点。模型中的5个参数Ms,a,α,c,k决定了磁滞回线的饱和特性和损耗特性。当变压器工作在饱和区时,磁滞回线的特性对变压器励磁电流畸变和磁滞损耗的大小很大影响。因此,准确地辨识J-A模型参数对研究变压器非正常状态下励磁电流的特征是非常重要的。
文献[3-4]通过公式推导,利用迭代求解的方法,由磁滞回线的8个特征参数求解J-A模型中的参数,但磁滞回线的特征参数需要用专业设备测量,工程上往往很难获得。文献[5]利用遗传算法和神经网络对J-A模型参数进行了辨识。本文根据J-A模型参数与磁化曲线形状的关系,提出了将模型参数分为2组辨识的新方法,首先利用单值磁化曲线对Langevin函数中的2个参数进行了辨识,然后利用磁滞回线对剩余的3个参数进行辨识,这样做缩小了辨识范围,提高了求解速度。本文将辨识出的磁滞回线与实验测得的磁滞回线进行对比,检验参数求解的准确性。该辨识方法已成功应用于变压器偏磁饱和的仿真中。
1 Jiles-Atherton磁滞回线模型
根据J-A模型[2],磁化强度M可以分为可逆磁化强度Mrev和不可逆磁化强度Mirr2部分,整个模型的方程如下。

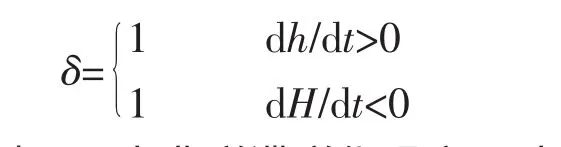
式中,Man为非磁滞磁化强度;H为磁场强度;δ为方向参数。5个模型参数分别为形状参数a,磁滞损失参数k,平均场参数α,磁畴壁弯曲常数c和饱和磁化强度Ms。式(2)称为Langevin函数,描述了磁滞回线的饱和性质。仿真分析表明,Ms决定磁化强度M的最大值。a为表征非磁滞磁化曲线形状的参数,a越大,磁滞回线的倾斜度越小。α参数反映磁畴间的耦合,α越大,磁滞回线的倾斜度越大。c和k值关系到磁滞回线的面积,c越大磁滞回线的面积越小,k值的作用与c相反。可见,磁滞回线的饱和特性主要由Ms和a决定,损耗特性主要由c和k值决定。本文正是基于J-A模型的这种特点,先由单值磁化曲线辨识Ms和a,再由磁滞回线辨识α、c和k。
2 基于MATLAB的参数辨识方法
MATLAB遗传算法工具箱可以方便地求解函数f(x)的最小值。本文通过编写模型函数和误差函数,将J-A模型与遗传算法工具箱结合,见图1。在GA工具箱的控制下,模型函数由传入的参数个体产生磁滞回线,误差函数将产生的磁滞回线与实测值进行对比,最终求得使误差函数最小的最优个体。

图1 辨识方法原理图
一般硅钢片的电磁特性都是由单值B-H的形式给出。Langevin函数(5)可以较为精确地描述单值磁化曲线,且函数中仅含有Bs和a 2个参数。在单值磁化曲线上取N个点(Hi,Bi),构建误差函数(6),即可利用MATLAB遗传算法工具箱对Bs和a进行辨识。

图2是对27JGSD095型硅钢片的辨识结果:Bs=1.93,a=6.098,ΔB=0.1197。

图2 单值磁化曲线辨识结果
J-A理论需要的是M-H曲线。通过式(7)~(12)将B-H曲线转化为M-H曲线。设已知的B-H曲线为
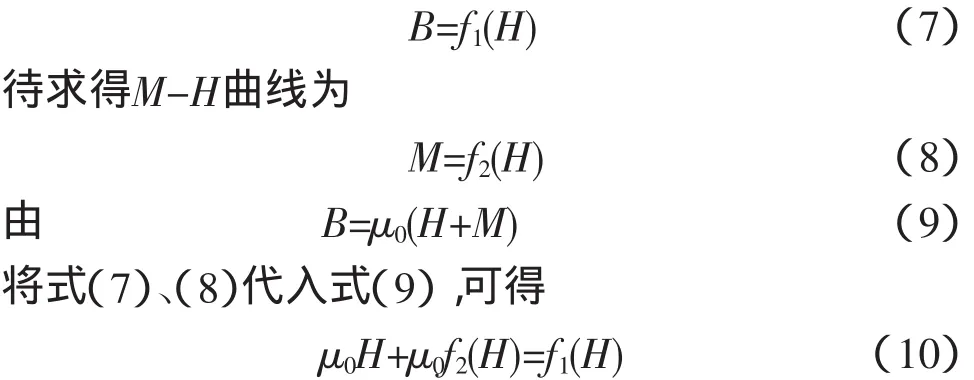
因为μ0=4π×10-7,对于电工硅钢片,通常H<500,所以μ0H≈0。由式(10)可得

通过上述辨识与推导,可以得到27JGSD095型硅钢片Ms=1.545×106,a=6.098。剩余3个参数主要描述了磁滞回线的损耗特性,辨识需要利用实际测量到的磁滞回线。
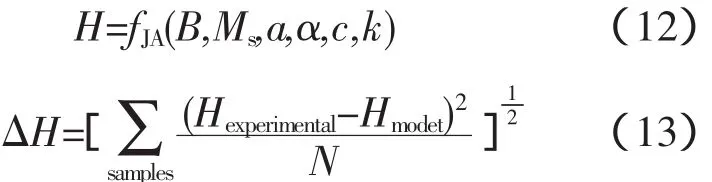
式(12)、(13)分别给出了模型函数和误差函数。通过遗传算法工具箱可以对模型函数中的参数进行辨识,其中Ms和a已在上节辨识得到,为常数。
3 算例仿真验证
为了验证本文提出的方法的有效性,利用参数Ms=1.51×106,a=6.5,α=13.9×10-6,c=0.4,k=21.9189,生成一条磁滞回线(图3),并对其参数进行辨识,辨识结果见图4,表1。

图3 待辨识磁滞回线
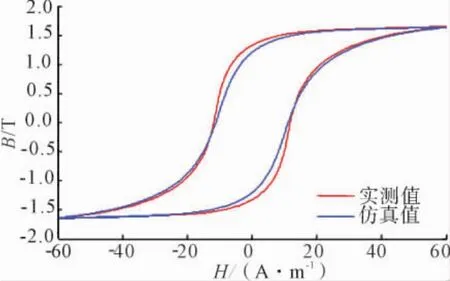
图4 给定参数的磁滞回线辨识结果

表1 给定参数的磁滞回线辨识结果
辨识结果表明参数辨识值与原始值差别不大,磁滞回线图形比较吻合。笔者对27JGSD095型硅钢片的磁滞回线(图5)进行了参数辨识。综合饱和特性参数辨识的结果,27JGSD095型硅钢片(Bmax=1.5T)的J-A模型仿真参数为Ms=1.545×106,a=6.098,α=1.0584×10-5,c=0.467,k=5.83304,仿真辨识结果见图6。各代的误差函数值见图7。仿真回线与实测回线相当吻合,因此本文提出的辨识方法是有效的。

图5 27JGSD095磁滞回线
4 结论
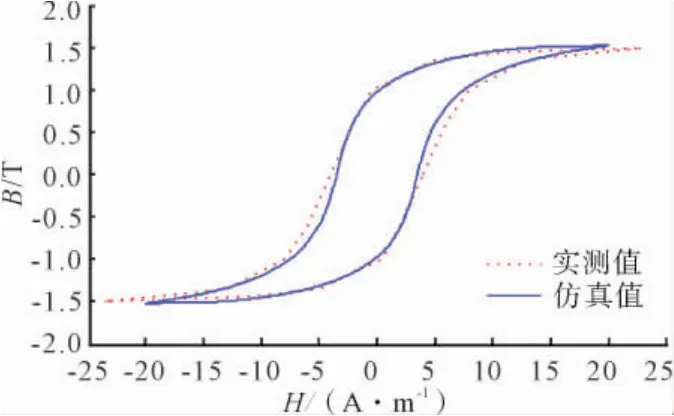
图6 27JGSD095辨识结果
图7 各代的误差函数值
本文提出一种Jiles-Atherton磁滞回线模型参数辨识的新方法:将磁滞回线特征分为饱和特性和损耗特性,利用单值磁化曲线(饱和特性)辨识Ms和a,利用磁滞回线(损耗特性)辨识α,c,k。这样做减小了辨识范围,提高了计算速度。通过对比给定参数磁滞回线和27JGSD095型硅钢片磁滞回线(Bmax=1.5T)辨识与仿真结果表明本文提出的方法是有效的。
[1Naidu S R.Simulation of the Hysteresis Phenomenon Using Preisach’s Theory[C]//IEE Proc,1990,137(2):73-79.
[2]JilesDC,AthertonDL.TheoryofFerromagnetic Hysteresis[J].JournalofMagnetismandMagneticMaterials,1986,61:48-60.
[3]Jiles D C,Thoelke J B.Numerical Determination of HysteresisParametersforthe Modeling of Magnetic Properties Using the Theory of Ferromagnetic Hysteresis[J].IEEE Transactions on Magnetics,1992,28(1):27-35.
[4]熊林,苏建仓.磁性材料磁滞回线模型参数的计算[J].真空电子技术,2004(3):16-18.
[5]Salvini A,Fulginei F R.Genetic Algorithms and Neural Networks Generalizing the Jiles-Atherton Model of Static Hysteresis for Dynamic Loops[J].IEEE Transcation on Magnetics,2002,38(2):873-876.
Identification of Transformer Core Hysteresis Loop Model Parameters
YUAN Zhong-chen,LIU Lian-guang
(Dept.of Electrical and Electronic Engineering,North China Electric Power University,Beijing 102206,China)
By means of the MATLAB genetic algorithm toolbox, model parameters are divided into two groups by the hysteresis loop measured by experiment.Then the 5 parameters in the Jiles-Atherton model are identified by hysteresis loop saturation and loss characteristics. The effectiveness of the method proposed in this paper is verified through a concrete example. The simulation results show that the method fits the hysteresis loop well.
hysteresisloop;Jiles-Atherton theory;parameter identification;genetic algorithm
利用MATLAB遗传算法工具箱,由实验测得的磁滞回线,将模型参数分为2组,分别通过磁滞回线饱和特性和损耗特性的方法,对Jiles-Atherton(J-A)模型中的5个模型参数进行了辨识,并应用具体实例对该方法的有效性进行了仿真验证。仿真结果表明,所提方法能较好拟合磁滞回线。
磁滞回线;Jiles-Atherton模型;参数辨识;遗传算法
国家高新技术研究发展计划(863计划)。
1674-3814(2010)09-0017-03
TM936.3
A
2010-08-18。
袁中琛(1985—),男,硕士研究生,研究方向为变压器直流偏磁影响;
刘连光(1954—),男,教授,博士生导师,主要研究领域为电力系统运行与控制。
(编辑 冯 露)
