基于诱导有序加权调和平均算子和马尔科夫链的电量组合预测模型的研究

师亮云，刘家军，王明军，姚李孝

（1.榆林电力设计院，陕西榆林 719000；2.西安理工大学水利水电学院电力系，西安 710048）

基于诱导有序加权调和平均算子和马尔科夫链的电量组合预测模型的研究

师亮云1，刘家军2，王明军2，姚李孝2

（1.榆林电力设计院，陕西榆林 719000；2.西安理工大学水利水电学院电力系，西安 710048）

0 引言

在进行用电量负荷预测时，组合预测模型是一种行之有效的方法，它充分利用各单一模型预测方法的有用信息和优点,考虑了多种因素对电力负荷的影响，因此,组合预测方法得到的结果一般要优于单一模型预测方法的结果[1-3]。一般说来，现有的组合预测模型中各单项模型的权系数是由其种类的不同而决定的，权系数只与预测方法有关，而与时间无关。也就是说同一种单项预测方法在各个时点的权系数是一样的。然而这与实际情况并不相符，因为同一种单项预测方法在不同的时刻表现并不是完全相同，有可能在某一点预测精度较高，但是另外一点预测精度则较低[4-7]，为了解决该赋权方法的问题，于是引进诱导有序加权调和平均(IOWHA)算子，通过每个单项预测模型在样本区间范围内各个时点的预测精度的高低不同按顺序赋权，然后以误差平方和为准则建立新的组合预测模型，给出IOWHA的确定方法，该方法能够较好地符合实际情况，因而具有较高的精度[8-9]。

但采用IOWHA组合预测模型进行预测时，因为组合模型中权系数是由各单项模型在各个待预测时点的预测精度高低决定的，欲确定组合模型的权系数，首先应知道其预测精度的状态，而待预测时点的预测精度状态是未知的，因此如何将待预测时点的预测精度的状态合理的表述出来就是采用该模型时亟待解决的问题。

马尔科夫链[10-13]是马尔科夫过程的一种特殊情况，它是通过对不同状态的初始概率及状态之间的转移概率关系，来确定状态的变化趋势，从而达到预测未来的目的。本文将IOWHA与MC结合起来，通过MC将待预测时点的预测精度状态定性表述出来，然后再将其应用到IOWHA模型中，从而确定待预测时点上各个单项模型的权系数，实例表明，模型能够降低预测风险，具有较好的预测效果。

1 IOWHA定义

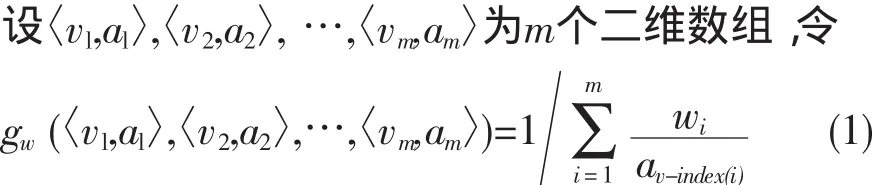
2 MC定义及基本原理

马尔科夫过程是无后效性的随机过程.当状态和时间参数都是离散时，称为马尔科夫链.根据年用电量需求预测的特点，可以将其近似看作状态和时间参数都是离散的马尔科夫过程。

若系统在t=n时间处于状态i，经过k次转移后在n+k时间处于状态j的概率为pij(k),则称pij(k)为k步转移概率,记作P(k)。不难证明，它可由一步转移率矩阵来表示,即：P(k)=Pk。

如果起始状态概率向量为P(0),经过k步后过程处于j状态的概率可用下式出

3 建模思想及步骤

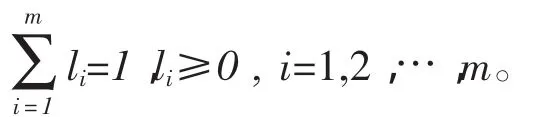
1）计算第i种方法第t时刻的预测精度ait，即

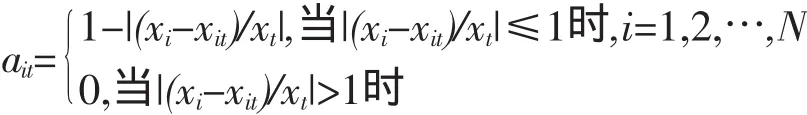
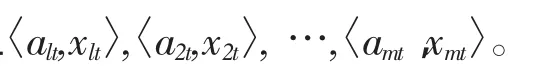
2）计算m种单项预测方法在第t时刻的IOWHA的组合预测值，即

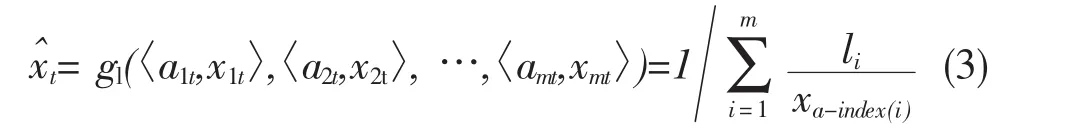
3）计算第t时刻组合预测模型的误差，令

4）以N期组合预测模型误差平方和最小为目标函数构成以下最优化模型：

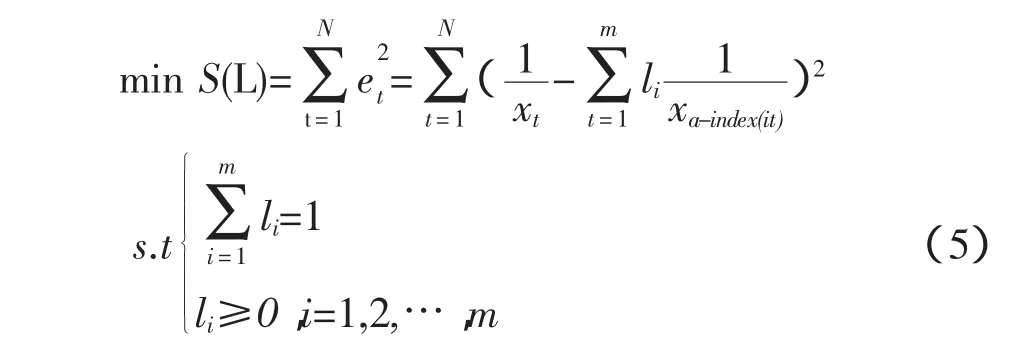
5）求解组合模型中m种单项模型的权系数l1,l2,…,lm，值得注意的是根据IOWHA组合预测模型特点：各个时点各单项模型的权系数只与预测精度有关，与各单项模型无关，由1）～5）即可建立IOWHA组合预测模型。

6）以预测精度为基准，划分若干状态空间。首先由组合模型中各单项模型预测精度的最大值和最小值得到其变化区间，然后按照聚类分析思想，认为预测精度相近的点为同一状态，进而划定合适的步长后，就可以得到各单项模型在各时点预测精度的状态。

7）根据预测期数T的不同，按照预测要求，构造不同的T步状态转移概率矩阵，即P(1),P(2),…,P(T)。

8）由最后一个历史点的状态以及所确定的状态转移概率矩阵,就可以得出未来的转移状态。因为组合模型中权系数是由各单项模型在各个待预测时点的预测精度高低决定的，欲确定组合模型的权系数，首先应知道其预测精度的状态，在判定组合模型中各单项模型的预测精度状态时，若转移概率矩阵中各个单项模型的状态不同，则直接按照状态定义排序即可；如果状态相同，但是转移概率不同，则转移概率大的预测精度高；若状态相同，转移概率也相同，则按照各单项模型相同状态的近几期内的预测精度的均值进行排序，例如：如果样本区间上最后一个历史点处于状态2，预测3期，则按状态2内近3期的概率均值进行排序。

9）由上述步骤得到各单项模型预测精度的高低顺序，进而得到组合模型的权系数，从而进行预测。

4 实例证明

为了反映本文基于诱导有序加权调和平均算子和马尔科夫链的电量组合预测模型的合理性，选择以下5个误差指标进行预测效果的分析。

1）平方和误差

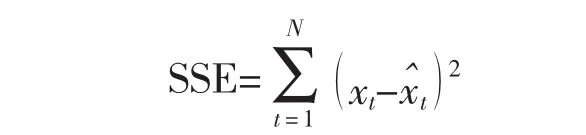
2）均方误差

本算例是来自陕西省某市1994—2009年年用电量的历史数据，对其分别采用回归分析法、指数平滑法及灰色预测法进行预测，其中2007—2009年的数据为待检验的数据，具体负荷历史数据及各种方法的预测值结果见表1。

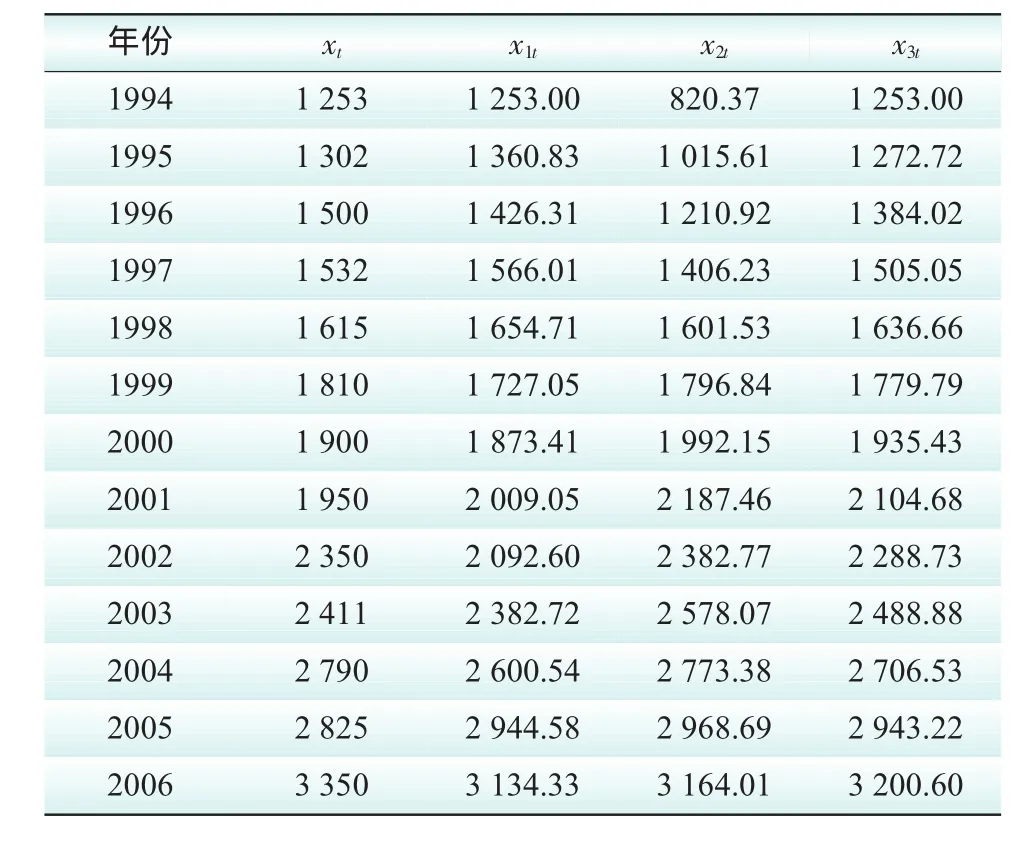
表1 实际值和3种单项预测方法预测值 万kW·h

根据表1负荷的历史数据建立的线性回归方程为Y=624.9990015+195.3080322t，其中Y和t分别代表各年年用电量和时间。灰色模型方程为YGM=14553.890102exp（0.083835×t）－13300.890102，其中YGM和t分别代表各年年用电量的累加数列和时间。

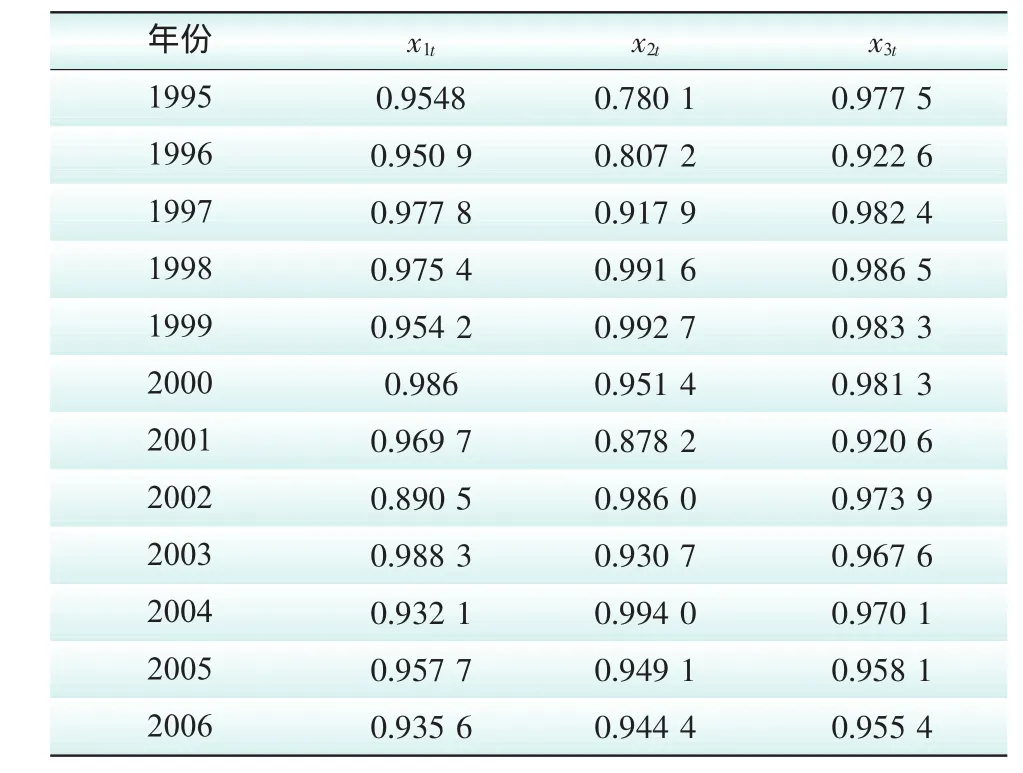
表23 种单项预测方法预测精度

按式(3)计算IOWHA组合预测值，下面简要说明计算过程：

同理可求得剩下其余各个时点的组合模型预测值。

将其带入式（5）中，经整理化简得如下最优化模型：

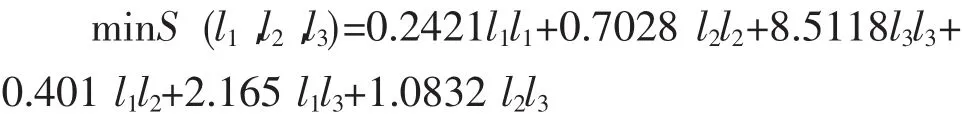
利用lingo软件计算出相应的组合预测权系数为l1=0.9235154，l2=0.0764846，l3=0。

如果以常用的基于误差平方和最小为准则的组合预测模型，可得如下最优化模型：

利用lingo软件计算出相应的组合预测权系数为l1=0,l2=0,l3=1。

基于诱导有序加权调和平均算子和马尔科夫链组合模型的预测效果评价的五个误差指标的计算结果如表3所示，从表3来看，各个单项预测方法的评价指标值均明显高于x6t的评价指标值，而且x6t与x4t和x5t相比在预测精度上也有一定程度的提高。

表3 预测效果评价指标体系

5 采用MC定性分析预测误差

根据表2，以预测精度为基准，对其进行状态空间的划分，各状态空间划分范围如下：状态1＜0.94，0.94≤状态2≤0.96，状态3＞0.96，如表4所示。

表43 种单项预测方法状态空间的划分

因为需要预测的2007年的预测精度未知，所以2006年在计算时不参与，由表4可得到3种单项预测方法各精度状态的元素个数，如表5所示。

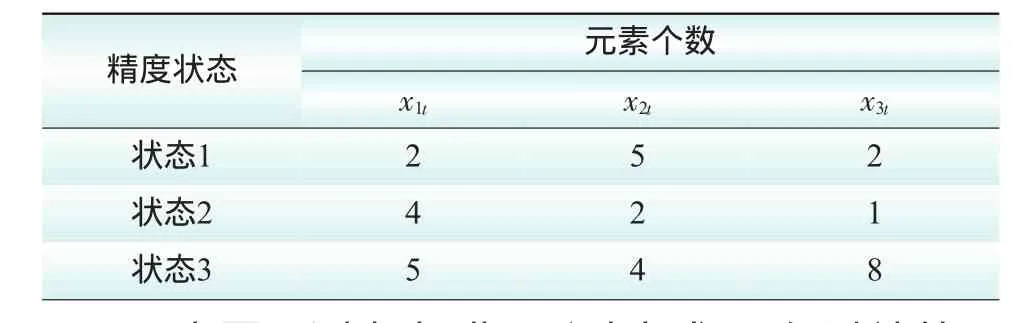
表5 采用单项预测方法得到的各精度状态的元素个数

因为要预测未来3期，所以由式（2）经过计算可得到各单项模型的1步至3步转移概率矩阵，指数平滑法的MC一步转移概率矩阵

2006年x1t，x2t和x3t的预测精度状态分别为状态1、状态2和状态2。由各单项模型的初始状态概率及一步至三步状态概率转移矩阵可得到未来3期中各单项模型的预测精度状态大致描述如表6所示。

由表6各单项模型预测精度状态的划分可以知道其预测精度的高低顺序，经过分析可知2007年各单项模型的预测精度顺序为x1t>x3t>x2t，同理2008年和2009年各单项模型的预测精度顺序也为x1t>x3t>x2t，因此进而可以确定组合模型的权系数。组合模型为YIOWHA=1/(0.9235154/X1t+0.0764846/X3t)

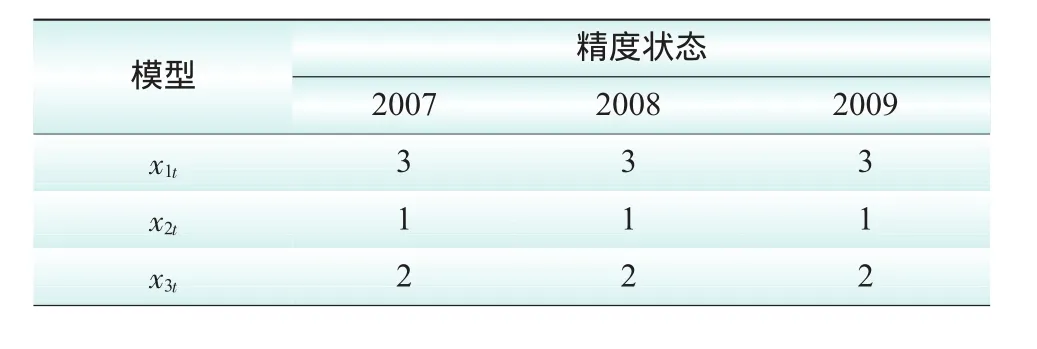
表6 各单项模型在预测期间的精度推测

6 预测结果分析及检验

选用2007—2009年负荷历史数据检验模型的正确性，根据前面建立的方程可以得出各单项预测方法2007—2009年的负荷预测值，另由上节分析可得EW组合模型、基于误差平方和最小组合模型及IOWHA模型组合模型的预测值，如表7所示。

表7 各单项模型及组合预测模型得到的2007—2009年预测结果

同时由表7可以得出各单项模型及组合模型的相对误差值，如表8所示。

表8 各单项模型及组合预测模型得到的2007—2009年预测相对误差绝对值

由表8分析可知，以0.96划定预测精度状态2和预测精度状态3的分界线与实际的预测精度相比较有一定的出入，但是预测精度的高低顺序是满足要求的。同时采用组合预测模型后，明显的减少了各单项模型预测的风险，提高了预测精度，尤其采用IOWHA-MC模型后，预测精度范围都控制在了3%以内，说明了该组合模型具有良好的预测效果。

7 结论

本文基于诱导有序加权调和平均算子和马尔科夫链的概念，提出新的组合预测模型，并采用陕西省某市年用电量组合预测的算例来说明该组合预测模型的有效性和合理性，实例证明这种组合模型具有较好的实用性。但是，文中的实例也表明一个问题：在划分预测精度的状态空间时，如何选取合适的步长，正确确定其精度范围，并最终提高其组合模型预测性能，是一个有待研究的问题，另外，采用基于诱导有序加权调和平均算子组合模型时，具有一定的适用范围，一般要求样本的实际观察值的取值较大。因为需要计算样本数据的倒数误差，如果取值过小(如均小于1)，则倒数误差比较大，而组合模型的权系数对于其倒数误差具有敏感性，因此这样就会影响组合预测效果。此时最好采用诱导有序加权平均算子的组合预测模型。

[1]陈华友.组合预测方法有效性理论及其应用[M].北京：科学出版社，2007.

[2]刘昊,张艳,高鑫,等.基于RBF神经网络与模糊控制的短期负荷预测[J].电网与清洁能源,2009,25(10):62-66.

[3]张建华,邱威,刘念,等.正交设计灰色模型在年电力负荷预测中的应用[J].电网与清洁能源,2010,26(2):28-32.

[4]陈华友，刘春林.基于IOWA算子的组合预测方法[J].预测，2003(6)：61-65.

[5]陈华友，程蕾，张倩.基于相关系数的IOWA算子最优组合预测模型[C]//桂林：第四届中国不确定系统年会论文集，2006：235-241.

[6]胡彦，李秀美，陈华友.基于IOWA算子的税收组合预测模型[J].统计与决策，2009（10）：33-35.

[7]周礼刚，陈华友，丁子千，等.基于Theil不等系数的IOWGA算子组合预测模型[J].安徽大学学报：自然科学版，2010（1）:1-6.

[8]陈华友，刘春林，盛昭瀚.IOWHA算子及其在组合预测中的应用[J].中国管理科学,2004(5):36-41.

[9]程玲华.一类基于相关性指标的非线性组合预测方法[D].合肥：安徽大学，2006.

[10]刘殿海，杨勇平，杨昆，等.基于马尔科夫链的能源结构与污染物排放预测模型及其应用[J].中国电力,2006(3):8-13.

[11]SHI Zu-lin,SU Wang-sheng.Energy Use and Environmental Pollution in China[R].China-India-Japan-United States Cooperation to Promote Clean Air,2001.

[12]石文辉，别朝红，王锡凡.大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法[J].中国电机工程学报，2008，28(4)：9-15.

[13]高亚静，周明，李庚银.基于马尔可夫链和故障枚举法的可用输电能力计算[J].中国电机工程学报，2008，26(19)：41-46.

[14]龙瑞华，毛弋，毛李帆，等.基于诱导有序加权平均算子和马尔可夫链的中长期电力负荷组合预测模型[J].电网技术,2010（3）：150-156.

A Combination Model Based on Induced Ordered Weighted Harmonic Averaging Operator and Markov Chain for Electricity Consumption Forecast

SHI Liang-yun1,LIU Jia-jun2,WANG Ming-jun2,YAO Li-xiao2
(1.Yulin Electric Power Research Institute,Yulin 719000,Shaanxi Province,China;2.Institute of Water Resources and Hydro-Electric Engineering,Xi’an University of Technology,Xi’an 710048,Shaanxi Province,China)

This paper proposed a newcombination forecasting model based on the Induced Ordered Weighted Harmonic Averaging (IOWHA)operator and Markov chain (MC)by combining the IOWHA operator and MC.The model can overcome some deficiencies in weighting and using single error index as forecasting precision measure of traditional combination forecasting model,meanwhile,by using of MC the forecasted accuracy condition of each forecasting method at the forecasted time point can be qualitativelysurmised,thus its weight coefficient at the forecasted time point can be determined.This paper firstly respectively makes use of Regression,Exponential Smoothing and Grey forecasting to construct models depending on annual electricity consumption of one city in Shaanxi Province.Secondly,the combination forecasting model of annual electricity consumption is founded by using the IOWHA operator and MC,and then the demonstration analysis about annual electricity consumption in future is gived.The example result illustrated that the new model can improve forecasting precision effectively.Therefore,the risk of forecasting is reduced.The results of the example shows that the combination model possesses better practicability.

Induced Ordered Weighted Harmonic Averaging(IOWHA)operator;Markov Chain (MC);forecasting accuracy;combined forecasting；annual electricityconsumption

将诱导有序加权调和平均算子和马尔科夫链相结合,提出一种基于诱导有序加权调和平均算子和马尔科夫链的组合预测模型，该模型可以克服传统的组合预测方法赋予不变的权系数和以单一误差指标作为预测精度衡量的缺陷，同时采用马尔科夫链推出各单项预测模型在各个预测时间点预测精度的状态，从而得到组合模型的权系数。文中首先采用回归法、指数平滑法及灰色预测法分别建立了陕西省某市年用电量单项预测模型，随后引进诱导有序加权调和平均算子和马尔科夫链的概念，建立了年用电量的组合预测模型，并对年用电量进行了实证分析。实例分析表明了新模型能有效地提高组合预测精度,降低预测的风险性,从而证明这种组合模型具有较好的实用性。

诱导有序加权调和平均算子；马尔科夫链；预测精度；组合预测；年用电量

1674-3814（2010）09-0038-06

TM715

A

2010-08-25。

师亮云(1958—)，男，工程师，榆林电力设计院院长，主要研究方向为电力工程设计;

刘家军(1967—)，男，副教授，硕士生导师，主要研究方向为电力系统监控与调度自动化;

王明军(1984—)，男，硕士研究生，主要研究方向为电力系统的运行与控制。

（编辑 李 沈）