基于Rietveld无标样定量研究HMX的β→δ等温相变动力学*

薛 超,孙 杰,宋功保,康 彬,夏云霞

（1.西南科技大学材料科学与工程学院,四川 绵阳 621010;

2.中国工程物理研究院化工材料研究所,四川 绵阳 621900）

1,3 ,5 ,7 -四硝基-1,3,5,7-四氮杂环辛烷（HMX）是1种重要的高能硝胺类炸药,有α、β、γ和δ等4种晶型,每种晶型都可以不同的冷却速度从适当的溶液中重结晶制得[1]。常温常压下,稳定存在的β-HMX具有最高的能量和密度,感度也最小,因此炸药配方中均使用β-HMX。然而,在165～210℃的温度下,β-HMX将转化为感度较高的δ-HMX[2]。

HMX的β→δ相转变被认为与其热分解和爆炸有密切的联系。T.B.Brill等[3-4]的研究表明,HMX在发生爆轰前将发生β→δ相转变。HMX在由β相（单斜晶系）向δ相（六方晶系）发生转变时,分子环状结构从准椅式转变为准船式,将产生6%～7%的体积膨胀,并伴随着大量的晶格破坏,这种破坏使HMX的物理化学性能发生了很大变化。在晶体内部形成的热点和剪切带,提高了HMX的起爆感度,从而使HMX形成稳定爆轰[5]。因此,开展HMX的β→δ相变机理以及动力学研究对于掌握HMX的安全性和起爆可靠性具有重要意义。在早期的动力学研究中[6],通常假设HMX的相变过程遵循1级相变反应。L.B.Smilowitz等[7]研究了PBX9501（95%HMX,其他5%粘结剂组分为聚氨酯和硝基增塑剂）中HMX在相变时δ相的成核和生长机理,认为HMX的相变为1级相变,同时混杂的2级反应机制对相变的机理有决定性影响。B.F.Henson等[8]和L.B.Smilowitz等[9]建立了HMX相变的热力学和动力学模型,该模型包括2种平衡体系:（1）β和δ的成核过程,（2）β和δ的生长过程。此模型将相变前期活化能和逆过程中的平衡相变自由能联系起来,并将核生长过程的活化状态同介稳的熔融态之间建立关联。对于HMX的β→δ相变研究的主要手段有傅立叶红外（FTIR）、2次调谐激发（SHG）、差示扫描量热法（DSC）和XRD等,不同的测试技术在研究HMX相变时各有利弊。

Rietveld无标样定量分析对于晶态物质无需应用内标或标定工作曲线,解决了定量过程中难以寻找合适的内标以及引入内标有可能对HMX的相变产生影响等难题。它考虑并利用XRD图谱中全部的强度数据,而不仅仅是最强的衍射线,因而部分降低了初级消光效应和择优取向。因此,Rietveld无标样定量可提高定量相分析结果的准确性。本文中以 Rietveld无标样定量相分析为基础,利用原位XRD技术研究HMX的β→δ等温相变动力学。

1 实 验

1.1 仪 器

XRD衍射数据采用德国Bruker公司CuKα辐射源的D8 Advance型粉末衍射仪收集。使用万特探测器,中低温样品台,管电压为40 kV,管电流为 40 mA;扫描范围为10°～60°,步长为0.05°,每步时间为0.1 s。本实验中主要考察0.1℃/s升温条件下发生相变的温度,以及温度为191、193、195和197℃时的相变时间,温度波动幅度均为±0.1℃,将样品在常温下以0.1℃/s升温至实验温度,每隔一定时间开始扫描,以刚升温到实验温度时作为相变时间的零基准。

1.2 样 品

样品为普通HMX经重结晶后得到,电镜照片如图1所示,可以看出其形状规则,颗粒较均匀;采用美国Aglient220型高效液相色谱测定HMX的纯度为98.9%,RDX含量低于检测限,属于1级品;采用美国LS230型激光粒度分析仪测定平均粒度为20 μm;采用密度梯度管法测得23℃时平均密度为1.897 9 g/cm3,较接近理论密度1.905 g/cm3。

图1 HM X颗粒的扫描电子显微图像Fig.1 SEM picture of HMX particles

2 Rietveld无标样定量方法的基本原理

Rietveld无标样定量方法的原理如下:混合相的粉末衍射图谱是各组成物相的粉末衍射图谱的权重叠加,各物相在混合物中的体积分数或质量分数与比例因子S（也称权重因子）有关[10],因而可以用最小二乘方法调节结构原子参数和峰形参数,使计算峰形和观察峰形相符合,求出比例因子S,通过比例因子S与质量分数的关系,求得该物相在混合物中的含量。在2θi位置的计算强度和混合物中物相含量分别为

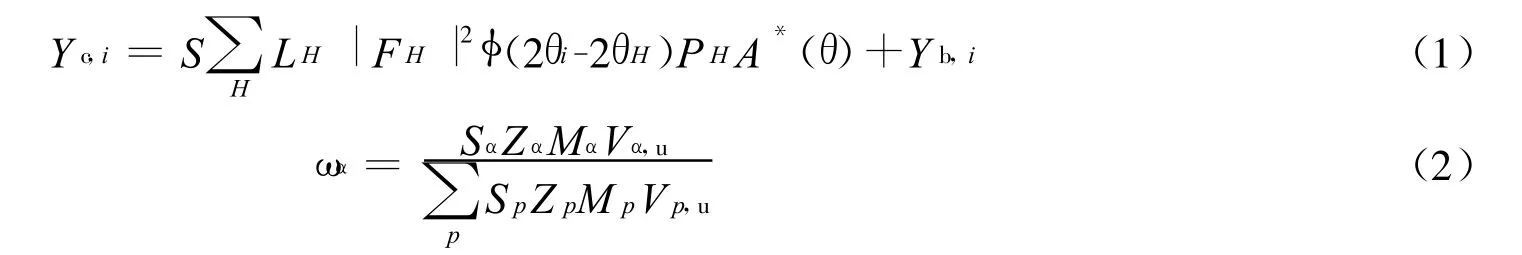
式中:Yc,i为2θi位置的计算强度,可能是几个布拉格衍射强度的叠加,H代表面指数为（hkl）的布拉格衍射,LH为面指数H衍射的洛伦兹因数、偏振因数和多重性因数3者的乘积,φ为衍射峰形函数,PH为择优取向函数,A*（θ）为试样吸收系数的倒数,Yb,i为背底强度,FH为H面指数布拉格衍射的结构因数（包括温度因数在内）。Sα、ωα、Mα、Zα和Vα,u分别表示α相的比例因子、质量分数、化学式质量、晶胞中所含化学式的量及其晶胞体积,∑p表示对样品中各物相加和[11-12]。

3 结果与讨论

3.1 升温相变过程

图2给出了HMX在0.1℃/s升温条件下β→δ相变时的部分XRD谱图,可以看出,在186℃时,HMX开始发生β→δ相变,210℃时转化完全。在186～210℃的温度区间内,β、δ相共存。表明HMX发生相变时不需要全部破坏β相就可以产生δ相,在一定的温度范围,2相是可以共存的,这为对XRD谱图进行2相定量进而研究相变动力学提供了保证。相关的标准谱对照,参见PDF卡片库42-1768（β-HMX）和44-1622（δ-HMX）。另外,在实验中发现,发生相变后的δ-HMX有些可以完全回复为β-HMX,有些却不能完全回复,回复的程度和速度与样品批次、实验条件有很大关系,产生这种现象的原因还有待进一步的研究。

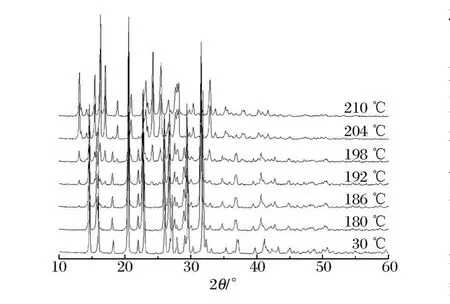
图2 升温过程中HMX的β→δ相变的XRD图谱Fig.2 XRD of β-δphase transition of HMX at elevated temperature

3.2 转变进度-时间曲线

HMX在等温条件下由β相转变为δ相的部分XRD数据如图3所示。从图中可以很明显地观察到,在一定温度下,随着恒温时间的增加,β相不断地转化为δ相。温度越高,相转变完成所需的时间越短。197℃时的相变过程,如图3（d）所示,由于过程非常迅速时间很短,7 min时δ相含量已达70%以上,因此不适合用XRD来进行动力学研究。通过在一系列的不同实验温度下观察整个相变过程可知,温度是影响相变的主导因素。

使用Bruker公司专用的Topas软件对各衍射谱进行物相定量,得出HMX在不同温度下转变进度与时间的关系曲线,如图4所示。初始引用的β-HMX和δ-HMX的结构参数见文献[14-15]。对各实验衍射谱进行物相定量时Rwp值均在11%～19%之间,在合理范围内[11]。

整个相变过程分为3个阶段:（1）诱导期大量的δ相晶核生成,为β→δ相变创造条件,图中并没有显示出来,这与实验温度有关。温度越低,完成相变所需时间越长,由于受实验时间的限制,本文中选择的最低等温相变温度为191℃,无法观察到诱导期;（2）自动催化期δ相开始生长且生长非常快,转变量迅速增大;（3）相变后期δ相含量很高,由于δ相被2相的相界面或体积膨胀时产生的应力所限制,相转变速率下降。

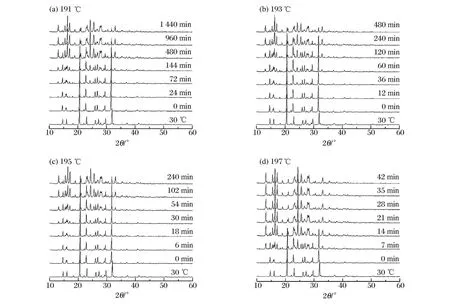
图3 HMX在不同温度下β→δ相变的XRD图谱Fig.3 XRD spectrograph ofβ-δphase transition of HMX at different temperatures

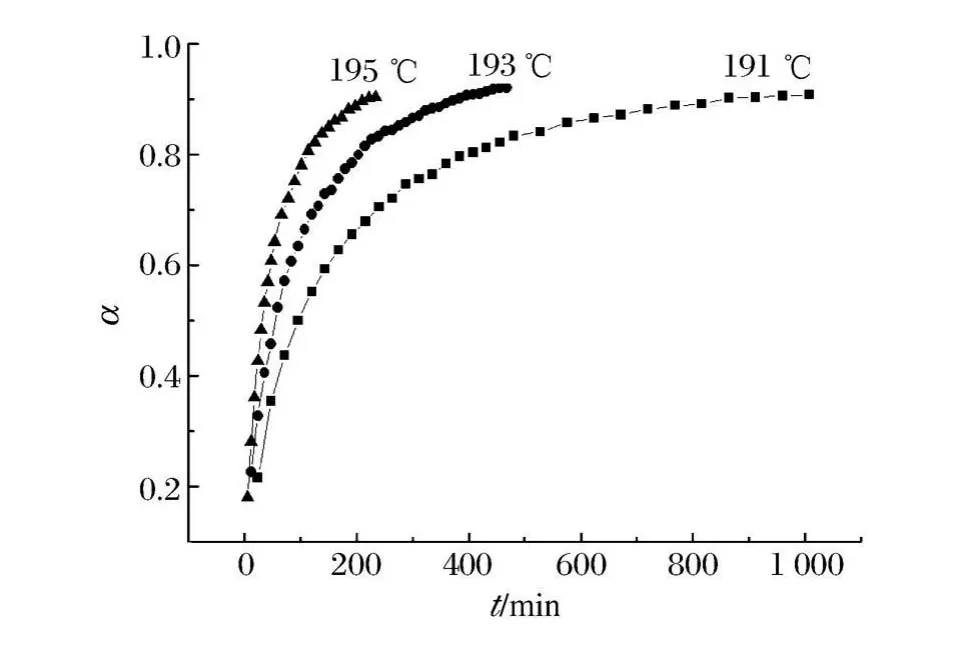
图4 HMX在不同等温温度的转变进度-时间曲线Fig.4 Transition extent versus time curves of HM X at different isothermal temperatures

3.3 动力学参数的计算

HMX的β→δ相变过程用Avrami方程[13]进行描述

式中:α代表t时刻β→δ相的转变分数,即转变进度;t为时间,单位为min;k（T）为温度T时的相变速率常数,包括成核速率与晶体生长速率,单位与Avrami指数n有关;n与相变的成核长大机制相关,对相变温度不敏感。

对公式（3）进行两边求对数,可得

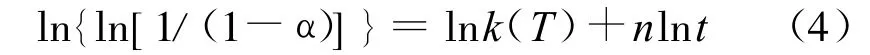
ln{ln[1/（1-α）]}与lnt的关系如图5所示,该对数图的斜率即为n值,截距即为lnk（T）。从图中可以看出,各温度下相变量在10%～90%区间内的ln{ln[1/（1-α）]}与lnt具有良好的线性关系,由此得出Avrami方程的指数n和速率常数k（T）,这样就可以得到HMX在不同温度等温时β→δ相变动力学方程

由以上数据可以看出,n值随温度升高略有增加,但增加的幅度很小,这是因为n值主要取决于δ相长大时的几何形状,从而只随几何形状变化而变化,k值则随温度的提高而增大,在影响HMX相变的诸多因素中,温度是起主导作用的。由得出的n值可以认为HMX发生β→δ相变时,δ相近似于1维随机成核长大,并混杂着在晶体内1个或2个位置处的优先成核,随后在这些位置逐渐开始长大。这些优先成核的位置应是晶体中成核势垒较低的空位、杂质或位错等缺陷处。

基于上述的结果,根据Arrhenius方程

式中:Ea为活化能,A为指前因子,T为开尔文温度。

对方程（5）两边求对数,可变换为

由以上得出的一系列k值做图6,分别求出斜率和截距,可得Ea约为151 kJ/mol,lnA为36.2。

图5 HMX在不同等温温度的转变进度-时间对数曲线Fig.5 ln{ln[1/（1-α）]}versus lnt curves of HMX at different isothermal temperatures

图 6 Arrhenius方程的Ea和 lnAFig.6 Values of Eaand lnA in Arrhenius equation

T.B.Brill等[4]采用FTIR研究了HMX的β→δ相变机理,并在1级相变的假设基础上得出活化能Ea=（204±14）kJ/mol和 lnA=19.9±1.0。L.B.Smilowitz等[7]使用 SHG 研究了PBX9501中HMX的β→δ相变动力学,求得活化能Ea=200 kJ/mol。R.K.Weese等[16]利用DSC分别用1级相变方程、Ozawa法和等转变率分析法对HMX的β→δ相变的动力学参数进行了计算,得出的活化能Ea≈500 kJ/mol,A=2×1048s-1。

本文中得出的Ea值稍低于T.B.Brill等[4]和L.B.Smilowitz等[7]得到的结果,同时远低于R.K.Weese等[16]得到的数值,这可能归结于以下几方面的原因:（1）由于在实验测量和数据处理方法上的差异性使得得出的结果存在偏差;（2）HMX的β→δ相变过程并非简单的1级反应,因此本文中得到的动力学参数与文献报道值会有所不同;（3）本文中经过重结晶后的HMX不同于T.B.Brill等[4]（含有少量RDX）和L.B.Smilowitz等[7]（95%HMX,其他5%粘结剂组分为聚氨酯和硝基增塑剂）使用的样品。

4 结 论

以Rietveld无标样定量相分析为基础,利用原位XRD技术研究了HMX的等温相变动力学,通过对β-HMX的转变进度与时间的关系曲线进行描述,得出了HMX等温相变的动力学方程。由Avrami指数n约为0.6,可以认为HMX发生β→δ相变过程中,δ相近似于1维随机成核长大。利用Arrhenius方程计算了活化能Ea和指前因子A,并与以前的文献进行了比较,分析了几项可能导致数据偏差的原因。

利用原位XRD来研究HMX的β→δ相变是一种可行的实验方法,但也存在着一些固有的缺陷,在XRD谱图扫描过程中,相变是连续发生的,谱图表现出的实际是相变的混合过程,在应用于其他相变研究时,必须制订合适的扫描策略。扫描时间长,不能实时地反映相变过程,扫描时间短,则不利于定量结果的准确性。

本研究的定量分析工作得到了中国科学院物理研究所骆军老师和深圳大学刘福生老师的大力协助,在此向他们表示衷心感谢。

[1] McCrone W C.Crystallographic data:Cyclotetramethylene tetranitramine（HMX）[J].Analytical Chemistry,1950,22（9）:1225-1226.

[2] Cady H H,Smith L C.Studies on the polymorphs of HMX[R].LAMS-2652,1962.

[3] Brill T B,Reese C O.Analysis of intra-and intermolecular interactions relating to the thermophysical behavior of α-,β-,and δ-octahydro-1,3,5,7-tetranitro-1,3,5,7-tetraazocine[J].The Journal of Physical Chemistry,1980,84（11）:1376-1380.

[4] Brill T B,Karpowicz R J.Solid phase transition kinetics:The role of intermolecular forces in the condensed-phase decomposition of octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine[J].The Journal of Physical Chemistry,1982,86（21）:4260-4265.

[5] Karpowicz R J,Brill T B.The beta to delta transformation of HMX:Its thermal analysis and relationship to propellants[J].AIAA Journal,1982,20（11）:1586-1591.

[6] Karpowicz R J,Brill T B.Kinetic data for solid phase transition by Fourier transform infrared spectroscopy[J].Applied Spectroscopy,1983,37（1）:79-81.

[7] Smilowitz L B,Henson B F,Asay B W,et al.Kinetics of theβ→δphase transition in PBX9501[C]//The Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter.Atlanta,Georgia,USA.2001:1077-1080.

[8] Henson B F,Smilowitz L B,Asay B W,et al.The β →δphase transition in the energetic nitramine octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine:Thermodynamics[J].Journal of Chemical Physics,2002,117（8）:3780-3788.

[9] Smilowitz L B,Henson B F,Asay B W,et al.The β →δphase transition in the energetic nitramine octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine:Kinetics[J].Journal of Chemical Physics,2002,117（8）:3789-3798.

[10] 梁敬魁.粉末衍射法测定晶体结构[M].北京:科学出版社,2003.

[11] 马礼敦.近代X射线多晶体衍射——实验技术与数据分析[M].北京:化学出版社,2004.

[12] Hill R J,Howard C J.Quantitative phase analysis from neutron powder diffraction data using the Rietveld method[J].Journal of Applied Crystallography,1987,20:467-474.

[13] Avrami M J.Kinetics of phase change（II）:T ransformation-time relations for random distribution of nuclei[J].Journal of Chemical Physics,1940,8:212-224.

[14] Choi C S,Boutin H P.A study of the crystal structure ofβ-cyclotetramethylene tetranitramine by neutron diffraction[J].Acta Crystallographica:B,1970,26:1235-1240.

[15] Cobbledick R E,Small R W H.The crystal structure of theδ-form of 1,3,5,7-tetranitro-1,3,5,7-tetraazocine（δ-HMX）[J].Acta Crystallographica:B,1974,30:1918-1922.

[16] Weese R K,Maienschein J L,Perrino C T.Kinetics of the β →δsolid-solid phase transition of HMX,octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine[J].Thermochimica Acta,2003,401（1）:1-7.