泵房恒压模糊自整定PID控制系统仿真*

胡大勇，陈勇刚，宋乐鹏

（重庆科技学院，重庆401331）

1 引言

泵房作为水厂的主要组成部分，其设备的监测与控制在水厂自动控制系统中具有重要的地位。在供水等企业中，泵机的电能消耗及设备的管理与维护的费用，在生产成本中占有很大的比例。如何降低水泵能耗，降低维修成本，对提高供水企业的经济效益有极其重要的意义。传统恒压供水控制系统大多采用PID控制技术，具有结构简单、易实现等优点，但由于泵房供水系统的模型带纯滞后的二阶大惯性环节，加之用户用水没有规律，这样系统模型参数具有很大的不确定性，因此很难建立精确的模型，不能满足一些精度要求高的供水系统，及实现节能的目的。本文提出恒压供水控制系统采用模糊自整定PID的控制策略并进行仿真，使系统的可靠性、稳定性、鲁棒性以及动态参数明显提高。

模糊控制最大的特点是将专家的经验和知识表示为语言控制规则，并用这些控制规则去控制系统，这样它可以不依赖于被控制对象的精确数学模型，能够克服非线性和时间滞后因素的影响，对被控制对象的参数具有较强的鲁棒性。模糊自整定PID是一种运用现代控制在线辨识对象特征参数，实时改变控制策略，使控制系统品质因素指标保持在最佳范围内，实现控制对象的最佳控制，其控制效果的好坏主要取决辨识模型的精度［1］。

2 系统结构及工作原理

当供水系统运行进入管网路时，压力变送器将压力信号与设定的各种压力给定值进行比较，把偏差传送给模糊控制器，根据误差e和误差变化率ec进行模糊推理，模糊过程中经自整定PID调节，再经反模糊化输出给执行机构（变频器）,由变频器控制水泵电机组的转速来调节管网压力，实现泵房恒压供水控制。对于多台机组联调，当用水量大于一台泵机的最大供水量时，通过PLC自动切换再起动其它的泵机，根据用水量的大小选择投入泵机组台数。如图1所示为泵房恒压控制原理图。

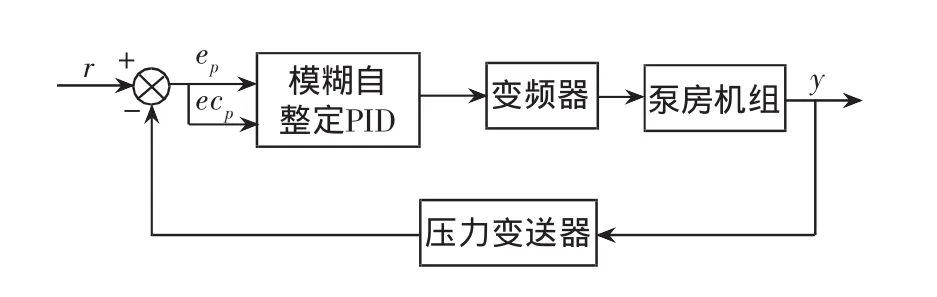
图1 泵房恒压控制原理图

3 带参数自整定模糊PID控制原理及结构［2］

PID模糊自整定在PID算法基础之上，通过计算当前系统偏差e和偏差变化率ec，利用模糊规则进行模糊推理，查询模糊矩阵表进行参数整定，代入下式计算当前 Kp、Ki、Kd：Kp＝Kp′＋{ei，eci}p，Ki＝Ki′＋{ei，eci}i,Kd＝Kd′＋{ei，eci}d。实现 PID 参数 Kp、Ki和 Kd的在线自整定。

PID控制器采用数字PID位置型算法：

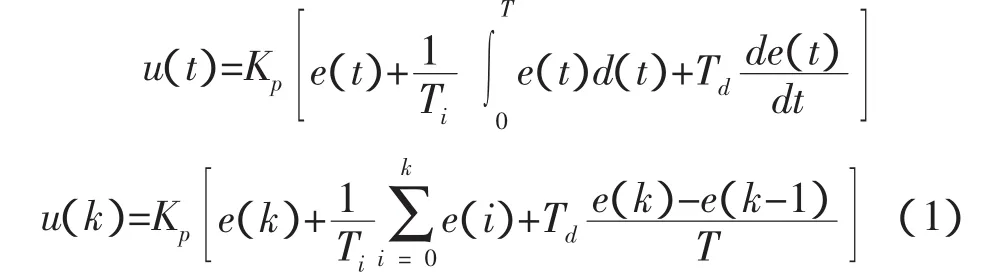
式中：u（k）、e（k）分别为第 k 次采样时刻控制器的输出（控制量）和输入量（误差）；Kp称为比例增益；Ti、Td分别为积分、微分时间常数；T为采样周期；Ki＝KpT/Ti称为积分系数；Kd＝KpTd/T称为微分系数。其结构模型如图2所示。

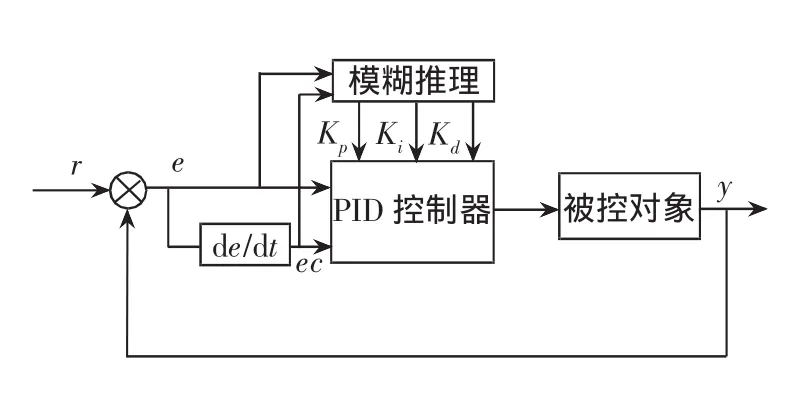
图2 参数自整定模糊PID控制结构图

4 带参数自整定模糊 PID 控制器设计［3］-［4］

模糊控制器是模糊控制系统核心。一个模糊控制系统的优劣主要取决于模糊器的结构、采用的模糊规则、合成推理算法，以及模糊决策等因素。本模糊控制系统采用二输入三输出模糊PID控制器，输入为压力e和压力变化ec，输出量为PID 3个参数（Kp、Ki、Kd）变化。

4.1 压力误差及误差变化率的模糊化

本设计分别用7个变量来描述输入输出，即｛NB，NM，NS，0，PS，PM，PB｝。输入语言变量模糊集论域取：｛-3，-2，-1，0，1，2，3｝。3 个输出语言变量模糊集论域分别取 Kp＝｛-3，-2，-1，0，1，2，3｝，Ki＝｛-2，-1.32，-0.66，0，0.66，1.32，2｝，Kd＝｛-1，-0.68，-0.34，0，0.34，0.68，1｝；选择三角函数、正态分布型隶属函数。其中NB、PB分别取Z型隶属度函数、S型隶属度函数，其余采用三角形隶属度函数。

4.2 PID参数整定原则

一般情况下，PID控制器的结构和算法已经确定，控制品质的好坏主要取决于控制参数选择的合理性。根据经验，从系统的响应速度、稳定性、超调量，稳态精度，Kp、Ki、Kd的作用等方面来考虑，对受控过程中对应不同偏差e和偏差变化率ec变化下，PID控制参数Kp、Ki、Kd的整定规则如下。

①当e较大时，为使系统具有好的快速跟踪性能，应取较大的Kp与较小的Kd，同时为避免系统响应出现较大的超调，应对积分作用加以限制，通常取 Ki＝0；

②当e和ec处于中等时，为使系统具有较小的超调，应取较小的Kp，Kd的取值对系统的影响较大，取适应的Ki；

③当e较小时，为使系统具有有较好的稳态性能，应取较大的Kp和Ki，Kd的取值要恰当，以避免在平衡点附近出现振荡。

4.3 模糊规则的建立与反模糊化

本控制器在操作人员（专家）长期实践积累的经验知识的基础上建立合适的模糊规则表，从而分别得到关于△Kp、△Ki、△Kd3个参数的模糊控制规则表,如表 1、2、3 所示。

模糊控制器采用重心法（COG）对模糊子集反模糊化。反模糊化采用加权平均求得反模糊化后输出的3个PID整定参数的精确的值。PID控制器根据实时整定输出的 3 个参数（△Kp、△Ki、△Kd），输出精确值信号给变频器，由变频器控制泵房机组。

表1 △Kp模糊控制规则表

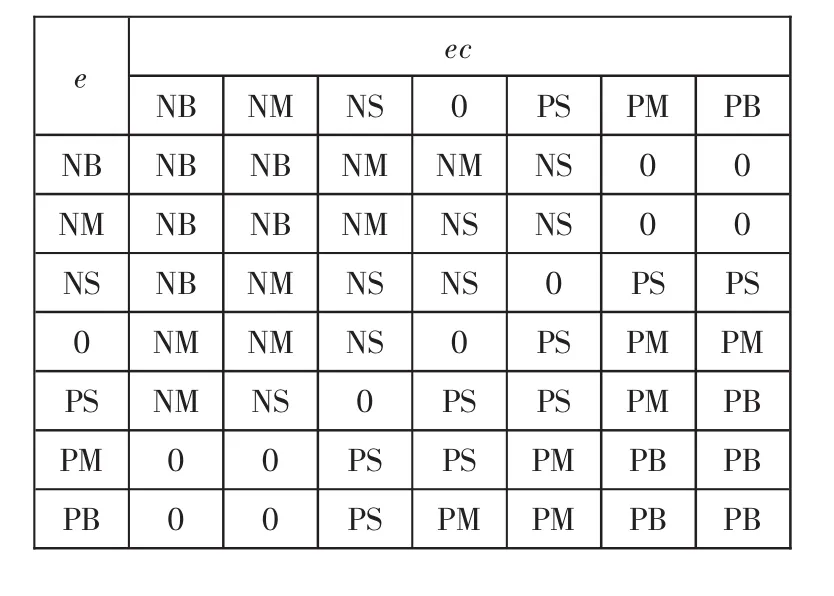
表2 △Ki模糊控制规则表

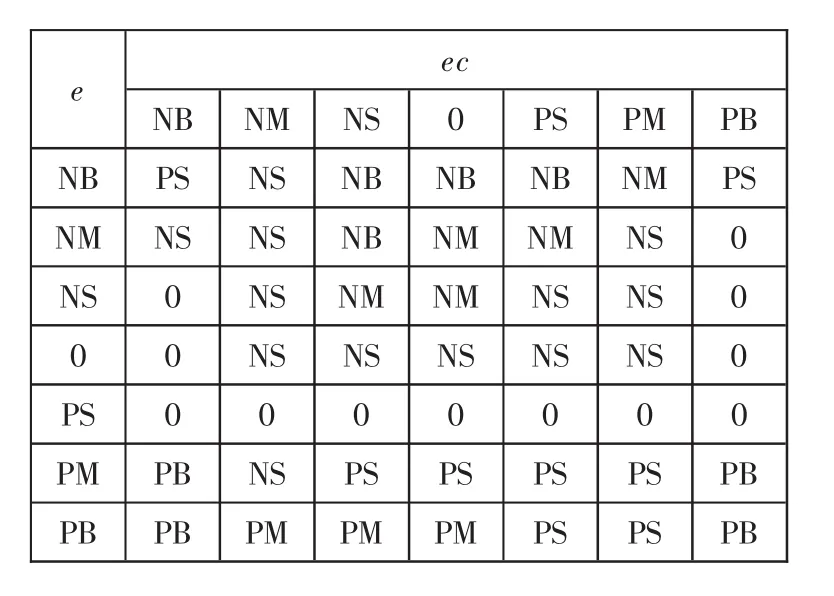
表3 △Kd模糊控制规则表

5 带参数自整定模糊PID控制器系统仿真

在Matlab环境下，利用模糊工具箱设计模糊控制器。在命令窗口键入：fuzzy，即打开模糊控制编辑器。然后在编辑器中建立二维输入三输出的Mamdani型控制器。根据上述自整定模糊PID控制器的设计，在Membership Function Editor界面分别输入 e、ec、Kp、Ki、Kd的隶属度函数和论域区间，其中e的隶属度函数曲线如图3所示。根据泵房恒压系统的控制经验，得到的模糊控制规则表，以if…and…then…形式在Rule Editor界面输入控制规则。选用加权平均法进行反模糊化。这样就建立了一个完整的FIS文件，保存文件取名为fuzzpid.fis，同时输出到工作工空间中。在Simulink中模糊控制器中添加fuzzpid完成模糊工具箱与Simulink的链接。上述过程在Matlab中很容易实现。本设计在Simulink中结合参数自整定模糊PID控制器模块建立泵房恒压系统仿真结构如图4所示。

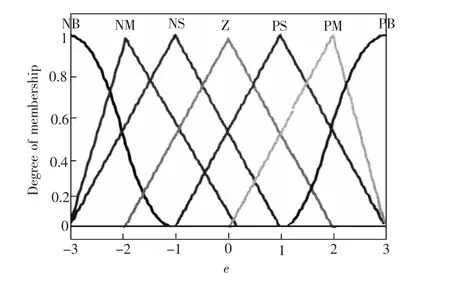
图3 隶属度函数曲线

6 变频恒压系统数学模型及仿真结果

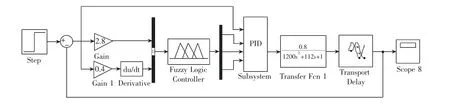
图4 泵房恒压系统仿真结构图

变频调速恒压供水系统是一个时变的、非线性的、滞后的被控对象。水泵由初始状态向管网供水，一般可分为零压过程和压力上升过程。零压过程中，水泵把水从清水池送到管网中，压力基本上可以认为保持为零是一个纯滞后过程；压力上升过程中,水泵把水充满整个管路,压力逐渐增加直至达到稳定,可以认为是一个一阶惯性环节。变频器和电机可近似等效为一阶惯性环节系统，其它的检测和控制环节，例如变送器、继电器控制转换可视为比例环节。因此该系统是一个二阶惯性环节、一个比例环节和一个纯滞环节组成，即系统的数学模型具有如下形式［5］：

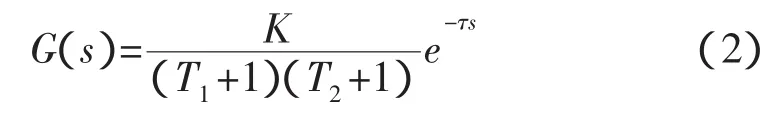
式中：K为系统的总增益,T1和T2分别为供水系统和变频器等的惯性时间常数，τ为系统滞后时间。

本文应用阶跃响应曲线法测试该系统的模型参数，经过对几次测量数据的拟合整理，确定K＝0.8，T1＝100，T2＝12，τ＝60s，采样时间 T＝10s。

在Matlab/Simulink中建立系统仿真模型，起动仿真，如图5所示。

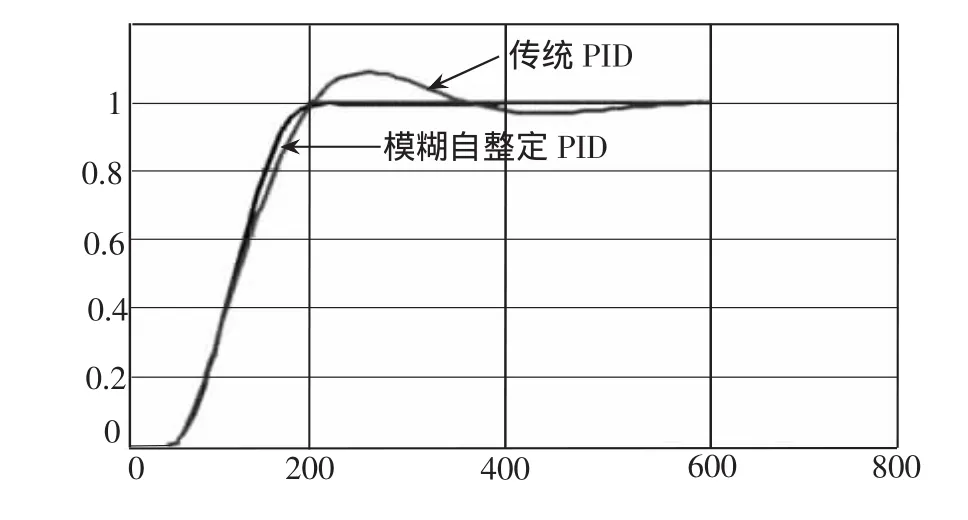
图5 泵房恒压系统阶跃响应曲线

由仿真得出的泵房恒压系统阶跃响应曲线，可知常规PID超调量为σ%＝8.6804%,上升时间tp＝260s，调节时间 ts＝510s；参数自整定模糊 PID 超调量为σ%≈0,调节时间ts≈180s。仿真结果表明参数自整定模糊PID较常规PID在泵房恒压系统具有更好的控制效果，基本无超调，调节时间快。

7 结论

本文提出的模糊自整定PID控制器在改善复杂大滞后泵房恒压系统在不同工况下的控制性能提供了一种有效方法。仿真实验表明，模糊自整定PID控制的可行性，模糊自整定PID控制和传统PID比较，具有输出响应时间快、调节时间短、无超调、稳态精度高，对参数具有较强的鲁棒性等优点，能够很好地解决泵房复杂大滞后系统由于用户用水没有规律等影响因素造成难题，从而产生较高的经济效益，为节约能源提供了好的途径。

［1］刘金琨.先进PID控制MATLAB仿真（第二版）［M］.北京：电子工业出版社，2007.

［2］C C LEE.Fuzzy Logic in Control Systems:Fuzzy Logic Controller-Part Iand Part II［M］.IEEE Trans on System，Man,and Cybernet-ics,1990,20（1）：419-425.

［3］李洪兴.四级倒立摆的变论域自适应模糊控制［J］.中国科学 E 集，2002,2（1）：65-75.

［4］李 旭，张殿华，何立平等.基于模糊自适应整定PID的活塞高度控制系统［J］.控制与决策，2006，（1）：97-101.

［5］吴锡福，宋根海，刘明远.稳压给水装置的设计探讨［J］.给水排水.1991,19.