基于SVM的船舶航向广义预测控制

施冬梅

（镇江市高等专科学校电子信息系，江苏镇江212003）

1 引言

航向控制是船舶操纵控制中最基本的，它的任务是保持航向和改变航向，航向控制直接关系到船舶航行的操纵性、经济性，它与航行安全、能源节约和操作省力密切相关。传统的船舶航向控制算法有PID控制、自适应控制。随着计算机技术和现代控制理论的发展出现了各种新的控制算法，如模型参考自适应控制、神经网络、模糊控制、模糊神经网络控制、变结构控制、广义模糊CMAC等算法。这些新的算法均先后应用于船舶航向控制中，但是大多数航向控制器的设计，人们普遍采用Nomoto线性模型进行设计，线性运动方程只适用于小扰动的情况。实际上，由于船舶本身存在的不确定性和风、浪、流等干扰，特别是对于不具有直航特性的船舶，在航向急剧改变的情况下，采用线性模型已经不能精确地描述系统的动态特性。本文针对常规自动舵响应速度慢，舵角操作不稳定，误差较大等缺陷，提出了将支持向量机系统辨识的方法与广义预测控制基本算法结合起来对船舶航向进行控制，以达到预期的控制效果。

2 SVM的基本原理

支持向量机是一种基于统计学习和结构风险最小化原理的学习机，其原理是在最小化样本点误差的同时，缩小模型预测误差的上界，从而提高模型的泛化能力。它不同于神经网络等传统方法以训练误差最小化作为优化目标，而是以训练误差作为优化问题的约束条件，以置信范围值最小化作为优化目标，因此，支持向量机的泛化能力要明显优越于神经网络等传统学习方法。另外，支持向量机的求解最后转化成二次规划问题的求解，因此，支持向量机的解是唯一的、也是全局最优的。正是上述两大优点，使得支持向量机一经提出就得到了广泛的重视，支持向量机方法在非线性系统辨识、预测预报、建模与控制等方面已取得广泛应用。

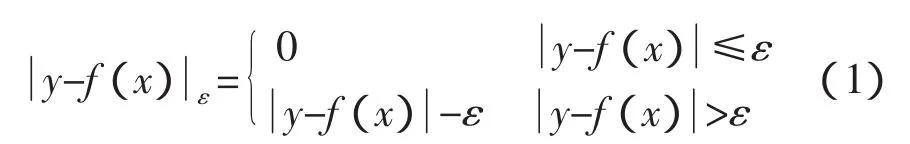
其中：f（x）为通过对样本集的学习而构造的回归估计函数，y为x对应的目标值，ε＞0为与函数估计精度直接相关的设计参数，该ε不敏感损失函数形象地比喻为ε通道。学习的目的是构造f（x），使之与目标之间的距离小于ε，同时函数的VC维最小，这样对于未知样本x，可最优地估计出对应的目标值。

对于训练集为非线性情况，通过某一非线性函数Φ（·）将训练集数据x映射到一个高维线性特征空间，在这个维数可能为无穷大的线性空间中构造回归估计函数，因此，在非线性情况，估计函数f（x）为如下形式：

其中：w的维数为特征空间维数（可能为无穷维）。最优化问题为：

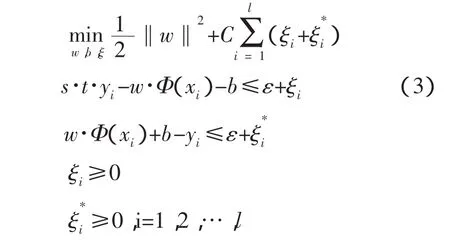
类似线性情况，得到对偶最优化问题

其中：b按如下计算

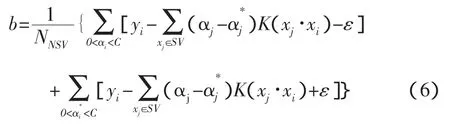
由式（5）和式（6）可知，尽管通过非线性函数将样本数据映射到具有高维甚至为无穷维的特征空间，但在计算回归估计函数时并不需要显式计算非线性函数，而只需要计算核函数，从而避免高维特征空间引起的维数灾问题。

3 SVM在船舶航向广义预测控制中的应用

设非线性系统由下面非线性离散时间模型表示：

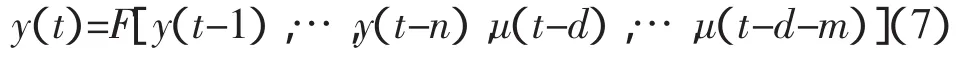
其中：n 和 m 分别是输出 y（t）和输入 u（t）的阶次，d是非线性系统的时滞，F（·）是一个未知的连续非线性函数。

支持向量机预测控制的实质就是利用作为对象辨识模型的支持向量机产生预测信号，然后利用优化算法求出控制矢量，从而实现对非线性系统的预测控制。如图1所示为SVM预测控制流程图。

图1 SVM预测控制流程图

广义预测控制具有实时预测、实时优化及实时反馈校正的特点而获得广泛应用。取优化指标为二次加权指标，广义预测控制器是通过在k时刻对下面的性能指标进行优化以获得控制作用。

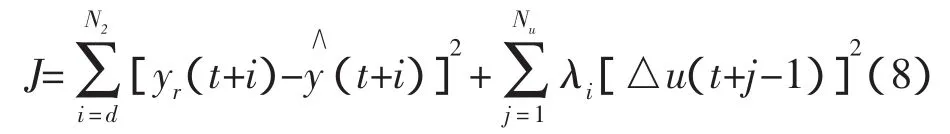
则在每一采样时刻，使用梯度下降法得△u控制律如下：

其中：μ是优化步长，并且

其 δyu＝

将式（11）代入到式（10）可得：

根据广义预测控制的滚动优化，广义预测控制律可取为：

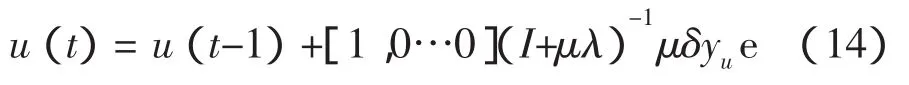
采用基于SVM的广义预测控制，对船舶模型进行仿真，船舶模型如下：

其中：τ1＝1、τ2＝0.5、α＝3、Kδ＝0.1、τ3＝0.5，ψ 为艏向角、δ为舵角。分别设定仿真时间为50s，研究船舶在25s时航向从10°变化到5°的实际航向历时变化曲线、控制舵角变化曲线和航向误差变化曲线。当系统无风、流、浪干扰时，仿真如图2、图3和图 4 所示（N2＝10，Nu＝5，λ＝0.01）；当系统有风、流、浪干扰时（采用有色噪声来模仿海浪干扰），仿真如图 5、图 6 和图7 所示（N2＝10，Nu＝5，λ＝0.01）。

图2 航向变化曲线

图3 控制舵角变化曲线

图4 航向误差变化曲线

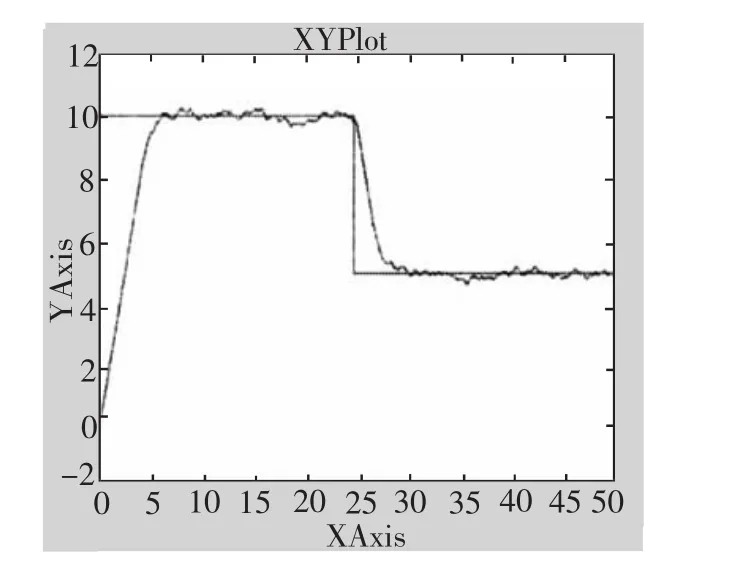
图5 航向变化曲线

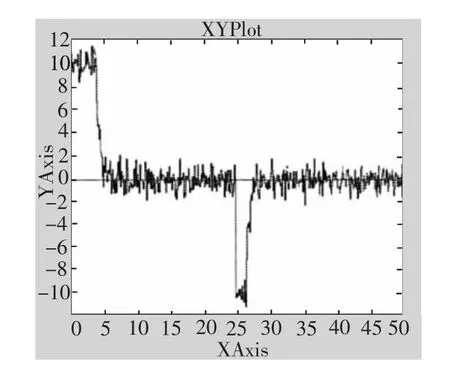
图6 控制舵角变化曲线

图7 航向误差变化曲线

4 结论

船舶航向控制是一个极为复杂的控制过程，船舶航向控制系统模型存在严重的非线性，且船舶在航行中，存在着模型参数与外界干扰的不确定性。本文将SVM运用到该领域的研究中，主要是利用SVM对非线性系统具有良好的函数逼近能力，善于联想、概括、类比和推理，并且具有很强的自学习能力、善于从大量统计资料中分析提取宏观统计规律的特点，仿真结果表明，基于SVM的广义预测控制算法对船舶航向的控制具有更好的稳定性和鲁棒性。

［1］陈建华.基于神经网络的非线性预测控制研究及其应用［D］.北京：华北电力大学硕士论文，2007.

［2］张浩然.基于支持向量机的非线性系统辨识［J］.系统仿真学报，2003，15（1）:119-121.

［3］庞中华.广义预测控制算法及其仿真研究［D］.青岛：青岛科技大学硕士论文，2005.

［4］秦永祥.基于自适应神经模糊系统的船舶航向控制［D］.大连：大连海事大学硕士学位论文，2007.

［5］林永屹.基于Backstepping的船舶航向非线性控制方法的研究［D］.大连：大连海事大学硕士学位论文，2007.