混凝土三维弹塑性本构模型研究
2010-06-15陈中生
陈中生
(深圳市市政设计院有限公司,广东深圳518000)
0 引言
随着国民经济的飞速发展,人们对建筑结构的要求越来越高,各种高层、超高层结构不断涌现。由于约束混凝土组合结构具有较高承载力和经济性,因而该组合结构在这些高层结构中的应用日益广泛。对这些约束混凝土构件进行精细化的三维有限元分析要求一类新的能够反映多轴应力下强度提高和剪涨效应的混凝土本构模型。在过去的几年里人们提出了各种混凝土的三维本构模型,例如Darwin等人[1]的较简单的非线性弹性经验模型,Bazant等人[2]提出的具有21个材料参数的复杂微平面模型等。对工程应用而言,一个成功的混凝土本构模型应该在精确性和适用性之间取得合理的平衡。本文介绍的模型能够较精确地描述混凝土三维应力状态下的行为且参数标定简单,适用于工程应用。该模型是在经典增量塑性理论下建立的,模型由加载屈服函数、强化函数、软化函数以及塑性流动函数组成。与经典塑性理论不同的是,该模型采用了塑性体积应变作为强化和软化的内变量,这样可以较好地描述混凝土的剪涨效应。模型中的各种材料参数最后都可以通过唯一的材料参数(混凝土的单轴压缩强度)来表示,从而使其应用极其方便。
1 塑性理论基本方程
根据经典塑性理论,在任意时刻的总应变增量可以分解为如下:

式中,dεe为弹性应变增量,dεp为塑性应变增量。
塑性应变增量可以通过流动法则确定,一般来说混凝土并不满足正交流动法则,因而本文采用了非关联流动法则,也就是说,塑性应变增量方向是塑性势函数的外法线方向,而不再与屈服面正交。因而塑性应变增量为:

为了方便计,下面的屈服函数和流动函数都是建立在Haigh-Westergaard应力空间的。该应力空间的基本参量是描述静水压力的长度参量ξ,应力偏量长度ρ,以及Lode角θ。本文建议的屈服函数基于Menetrey-Willam三参数屈服函数:

式中,k(κ)和c(κ)分别为混凝土的强化和软化函数,内摩擦系数m和椭圆偏心函数r(θ,e),定义为:

因而,用混凝土的单轴拉伸强度ft、单轴压缩强度fc及偏心率参数e就可以确定混凝土屈服函数在三维应力空间的大小和形状。通常根据《规范》混凝土的单轴拉伸强度取为其单轴压缩强度的0.1倍;理论上偏心率取值为0.5~1,Menetrey等人[3]建议混凝土的偏心率可以取为0.52,通过公式(3)可知这对应与混凝土的双轴强度和单轴强度比()为1.14,这对于普通混凝土而言具有足够的精。但是对于高强混凝土,不同标号的混凝土其稍有不同,因而偏心率稍有差别,根据试验资料回归得到的混凝土关系为:

因此不同标号的混凝土偏心率可以利用公式(5)和公式(3)求得。
2 混凝土的强化和软化函数
混凝土的强化和软化可以视为屈服面在应力空间形状和位置的变化,可以分别用强化函数k(κ)和软化函数c(κ)来描述。常规塑性理论强化和软参数往往取为等效塑性应变或塑性功,它表示起强化或软化作用的是塑性应变长度的某种度量,很难满意地描述混凝土多轴下的强度提高,往往得到的体积变形过大,不能反应围压的约束作用。鉴于此有的研究者就将强化参数与围压或塑性体积变形联系起来,以期能够反应随着围压增大混凝土的不断增强的变形能力,但是这需要增加材料参数,往往给塑性模型参数标定带来困难。既然混凝土的体积膨胀与约束有关,围压对混凝土的塑性变形能力有着重要的影响,因而其对合理描述混凝土的三轴变形行为相当关键[4]。Grassl等人[5]建议用塑性体积应变作为塑性参数并取得了较好的效果,因此塑性参数可以定义为:定义强化函数为:式中,εpv,t是混凝土单轴压缩峰值应力时的塑性体积应变,k0定义为混凝土单轴压缩初始屈服的强度与峰值强度比:



对于普通混凝土初始屈服强度大约是峰值强度的30%-40%。
随着混凝土塑性变形的进一步发展,塑性变形将会出现局部化,从而变形将会集中在某些特定的点在宏观上表现为混凝土的塑性软化。Grassl等人[5]建议塑性软化可以通过软化函数c(κ)描述:


式中,参数t控制软化速度定义为:
t=fc/15000 (11)
可见,定义了强化函数和软化函数后,混凝土的强化可以视为屈服函数在应力空间沿静水应力轴正方向的平移和膨胀,而混凝土的软化则可视为屈服函数在应力空间沿静水应力轴负方向的平移。
3 混凝土的流动函数
由于混凝土塑性变形存在剪胀效应,往往采用非关联流动法则,合理塑性势函数对描述混凝土的塑性变形至关重要。它控制着塑性流动的方向和塑性应变的累积。试验表明混凝土围压越大,混凝土的体积膨胀越小,约束效果越明显,合理的塑性流动函数应该能够反应这一点,即塑性流动函数在Haigh-Westergaard坐标中的子午线随着静水压力的增加不再是直线变化,而是变斜率的,逐渐偏向静水压力轴,使塑性体积应变的分量越来越小,从而增强混凝土的塑性变形能力。显然,基于直线变化的Drucker-Prager形式的塑性流动函数不能较好地反映这一点。Grassl等人给出了一种非线性塑性流动函数,随着围压增加(ξ增加),子午线不断向静水压力轴靠拢,曲线斜率不断减小,塑性体积分量越来越小,能够较好地描述围压对塑性变形的约束作用和混凝土强度的提高。Vassilis等人建议的流动函数为:

式中,材料参数A,B,C的标定可见Vassilis等人的工作。由此建立了混凝土的弹塑性本构模型,虽然在模型中出现了较多的材料参数,但是这些材料参数都可以在现有试验结果的基础上通过唯一的参数—混凝土单轴峰值强度进行标定,从而使模型工程应用极其方便。
4 数值计算
在混凝土的弹塑性数值求解上,Ortiz[6]等人建议了一类称为算子分离法的回映算法,为了减小迭代过程中重复计算Lee[7]等人在建议了对应力张量进行谱分解的方法,Vassilis[4]等人建议了一种后退Euler法的隐式积分算法,并且还采用了半分法来加快收敛速度,减小迭代计算量。由于完全隐式的后退Euler回映算法具有较高的精度可成熟的算法,本文采用了不同于Vassilis等人的半分法方法,采用完全隐式的后退Euler法求解提高了计算精度和稳定性。
基于对率形式的本构方程进行积分的算法称为应力更新算法,在完全隐式的算法中,在步骤结束时计算塑性应变和内变量的增量(后退欧拉算法),同时强化屈服条件。基本思路是先弹性预测,再按最近点投影塑性修正(回映算法),积分算法写为:

式中,rn+1是n+1时刻的流动方向,hn+1是n+1时刻的塑性硬化函数。将公式(13.b)代入(13.d)得到:
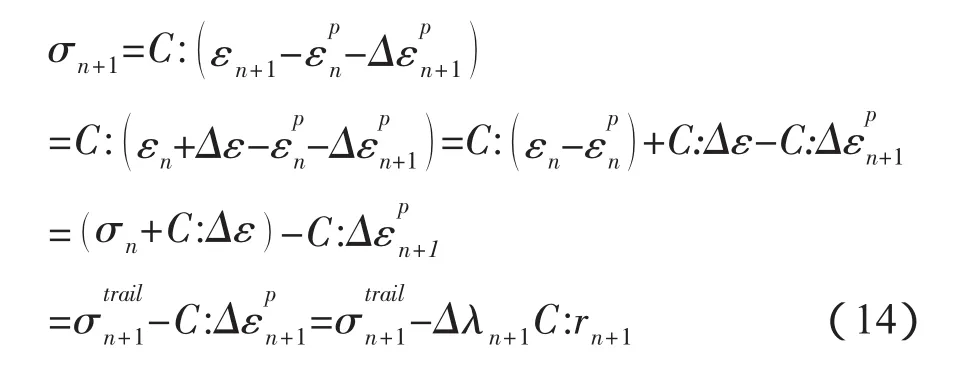

利用通用非线性有限元分析软件Abaqus的用户材料子程序接口(UMAT)可以将上述混凝土弹塑性本构模型嵌入到Abaqus中进行混凝土结构的弹塑性非线性分析。
5 模型计算结果
为了考察模型的性态和有效性,首先用Abaqus模拟了两组Dahl等人[8]关于混凝土的单轴受压应力-应变关系试验研究的结果,试验中两组混凝土的实测值分别为21.7 MPa及31.7 MPa;模型计算的峰值应力分别取为20.0 MPa及30.0 MPa。二者比较如图1所示,按照Abaqus的约定,受压符号为负,故下面各图均标示为负值,“Model”标示该模型计算结果,“Exp”标示试验结果。可以发现模型计算结果和试验结果在上升段、峰值应力和峰值应变吻合较好,下降段模型计算结果比试验稍有区别,考虑到试验离散型可以认为该模型可以很好地描述混凝土单轴应力-应变关系。

图2给出了单轴峰值强度分别为20 MPa、30 MPa、40 MPa、50 MPa、60 MPa、70 MPa、80 MPa的混凝土单轴应力-应变关系,图2中数值标示混凝土的单轴压缩峰值强度。

混凝土压缩的一个重要的现象就是体积膨胀,试验时随着荷载的不断增加,混凝土先经历了体积压实的过程,随后由于剪切破坏内部出现了较多裂纹,出现剪胀现象,剪胀现象见图3所示。图3中“volume”表示体积应变随单轴荷载变化关系。


约束对混凝土强度提高的效果在图4中得到集中体现,图4是强度为47.4 MPa的混凝土在不同约束应力下的应力-应变关系曲线。图中标示“uniaxial”表示单轴应力应变曲线关系,数值标示约束应力,如4.74 MPa标示约束应力为4.74 MPa时的应力应变关系,其他标示类似。可见随着约束应力的增加,混凝土强度有了显著的提高。
6 结语
上述混凝土弹塑性本构模型能够很好地描述混凝土的体积膨胀和围压对塑性变形的约束作用及强度提高,由于模型引进了椭圆方程,使屈服(破坏)子午线能够随相似角不断变化,从理论上来讲可以描述任何围压下的混凝土三维受力特点。由于塑性体积应变是围压的直接度量,用它作为强化,软化参数就可以直接反应围压的影响;同时塑性势函数在在Haigh-Westergaard坐标中,子午线是曲线变化的,相似角相关,使得高围压下混凝土的塑性体积变形得到了有效约束,强度得到提高。
[1]Darwin,D.,Pecknold,D.A..Nonlinear biaxial stress-strain law for concrete[J].Journal of Engineering Mechanics,ASCE.1977,103(2),229-241.
[2]Bazˇant,Z.P.,Prat,P.C.Microplane model for brittle-plastic material:I.Theory[J].Journal of Engineering Mechanics,ASCE.1988,114(10),1672-1688.
[3]Menetrey,P.,Willam,K.J.Triaxial failure criterion for concrete and its generalization[J].ACI Structural Journal.1995,92(3):311-318.
[4]Vassilis K.Papanikolaou,Andreas J.Kappos Confinement-sensitive plasticity constitutive model for concrete in triaxial compression[J].International Journal of Solids and Structures.2007,44:7021-7048.
[5]Grassl,P.,Lundgren,K.,Gylltoft,K.Concrete in compression:a plasticity theory with a novel hardening law[J].International Journal of Solids and Structures.2002,39(20):5205-5223.
[6]Ortiz M.,Simo J.C.An analysis of a new class of integration algorithms for elastoplastic constitutive relations[J].International Journal for numerical methods in engineering.1986,23:353-366.
[7]Lee,J.,Fenves,G.L.A return-mapping algorithm for plastic-damage models:3-D and plane stress formulation[J].International Journal of Numerical Methods in Engineering.2002,50:487-506.
[8]Dahl,K.K.B.A constitutive model for normal and high-strength concrete[C].ABKReportNo.R287,DepartmentofStructuralEngineering,Technical UniversityofDenmark,1992.
