双模导航接收机时间系统一致性研究

徐伯健,符京杨,敬必刚,朱克家

(中国人民解放军61081部队,北京100094)

0 引言

普通GPS接收机在某些地域使用存在一定的局限性。例如在山脉中或山地峡谷地形或者大范围原始森林地区进行地质勘查、测绘时,由于高山遮挡可见卫星数减少,或是由于受树木遮拦,卫星信号失锁的现象时有发生,从而无法完成定位。集成了双GNSS接收模块的接收机使得卫星数的可见数增加,在一些GPS信号薄弱的地区,该双模接收机大大提高了观测精度和数据可靠性。

但在使用GPS/GLONASS双系统组合测量中,只能使用其中一个时间系统作为基准来记录和处理观测数据。如果不考虑2个时间系统的差异,将为定位解带来系统差。因此,准确确定时间系统的差异及差异转化就成为集成模块接收机提高精度和可用性的关键。

1 时间系统及其相互关系

首先分析GPS时与GLONASS时在整秒上的关系。GPS时(GPST)属于原子时系统,其秒长与原子时相同,但与国际原子时(IAT)具有不同的原点。存在一个常量偏差,其关系为:

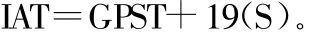
GPS时与UTC的时刻,规定于1980年1月6日0时(UTC)一致。由于GPST没有闰秒,其后随着时间的积累,二者之间的差别表现为秒的整数倍。二者的关系为:

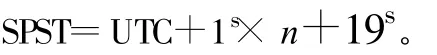
GLONASS时间(GLONASST),是以前苏联建立、俄罗斯维持的世界协调时UTC(SU)作为时间度量基准的UTC时间系统,也存在闰秒。GLONASST与UTC(SU)之间存在3 h的整数差。

由GLONASST与UTC的关系和GPST与UTC的关系可得:

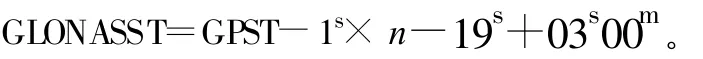
再来分析不足整秒的时间微小量。GPST以UTC(USN0)为时间度量基准UTC(USNO)与国际时间局(BIPM)维护的UTC(BIPM)的差别在20 ns。

GLONASST是以俄罗斯维持的世界协调时UTC(SU)作为时间度量基准。GLONASST与UTC(SU)在秒上,二者相差在1 ms以内,在GLONASS卫星发播的导航电文中有相关GLONASS时间与UTC(SU)的相关参数。UTC(SU)与国际标准UTC,相差在1 μ s以内。

通过分析比较GPST、GLONASST、UTC(USNO)、UTC(BIPM)、UTC(SU)等时间系统的差异,可以预测出GPST与GLONASST之间相差的微小量应在1 μ s以内。

2 时间系统一致性分析的方法

2.1 一致性分析概述

除了3 h的整数差值,GPS时间和GLONASS时间的差异还分为两部分:闰秒数和一个与时间有关的微小数值(慢变微小量)。闰秒数很容易得到,用户可从相关通报、通知和导航电文等途径提前知道闰秒日期。而这个微小的部分很难确定。对GPS和GLONASS时间系统一致性分析的重点在于确定慢变微小量。

在一个已知精确坐标的测站上,用户通过GLONASS/GPS双模系统接收机同时接收GLONASS和GPS的卫星信号,如果求得同一接收时刻接收机钟在2个系统下的钟差Δ、Δ,用户钟面时间唯一,从而得知GPS时和GLONASS时的差异ΔT即(Δ-Δ)。

2.2 一站单机测钟差法

某颗GPS卫星在时刻发射的GPS信号初相,通过电离层和对流层到达用户接收天线的时刻为ΔTua,则GPS信号传播时间为:

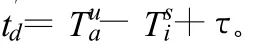
式中,τ为电离层和对流层时延,若发射时刻的GPS时为,又

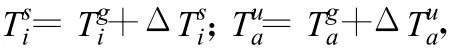
式中,ΔT=Δ-Δ为接收机钟面时与GPS时之差,则

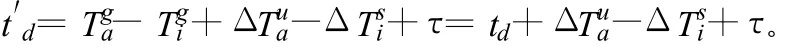
式中,td=-可认为是卫星信号的真实传播时间。

从而可得用户时钟偏差为:

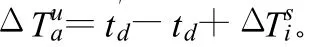
2.3 使用IGS和IGEX精密星历计算卫星位置

IGS(International GNSS Service)和IGEX(The International GLONASS Experiment)精密星历提供15 min和5 min间隔的精密星历钟差参数,而在实际接收机的采样率一般为30 s、15 s。因此,在数据处理中用户需选择合理的插值才能获得任意时刻卫星的位置。下面就拉格朗日插值的实现方法予以说明。

设在n+1个时间为t1,t2…tn+1,插值节点上卫星的坐标分别是x1(t1),x2(t2),…xn+1(tn+1),那么在任意时刻t卫星_的坐标可以表示为:

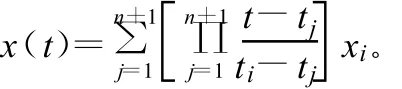
利用公式,在X、Y和Z方向上分别进行插值处理,即可得到任意时刻卫星的位置。

3 算例与分析

使用集成双模的GPS和GLONASS组合接收机在已知精确坐标的测站对GPS和GLONASS卫星进行观测。使用RINEX格式观测文件和SP3格式的IGS和 IGEX精密星历进行钟差解算。通过比较GPS和GLONASS系统下同一接收机的钟差来比较2个系统时间的差。

3.1 解算过程

测站坐标为WGS-84坐标系;使用伪距观测量ρ1、ρ2进行解算;确定观测时刻卫星位置使用拉格朗日插值法;IGEX精密星历所给坐标属于ITR97,与WGS-84坐标系差异很小,未进行坐标转换;IGEX和IGS精密星历给出的时间均为UTC时刻,所以计算过程中无须考虑时间系统整秒差异;对于电离层延迟的改正采用双频改正法:

对于GPS信号的改正为:

而对于GLONASS信号,因其不同卫星的频率不同,所以改正系数也不同。每颗卫星的频率为:

再根据公式进一步求得改正数;

采用Hopfield对流层改正模型来改正对流层折射延迟;卫星测量时刻的位置加入地球自转改正。

3.2 计算结果说明

通过软件对2009年12月22日双模GPS/GLONASS接收机获得的观测数据和IGS与IGEX提供的精密星历模拟计算出接收机钟差,其中:

将计算结果进行分析比较如下:

①解得的接收机钟差均在ms以内。在有些历元低至几μ s,在某些历元高至几百μ s;

②2个系统下的钟差之差(δt1,δt2)均为 μs级。这其中包含GPS和GLONASS时间系统的差异测量过程中的各种误差;

③接收机钟差均是随时间规律变化的。表1给出的结果显示接收机钟差的绝对值在不断减少。钟差之差(δt1,δt2)的变化不明显,保持较小的浮动。这也说明接收机的钟漂在2个系统中变化是一致的。

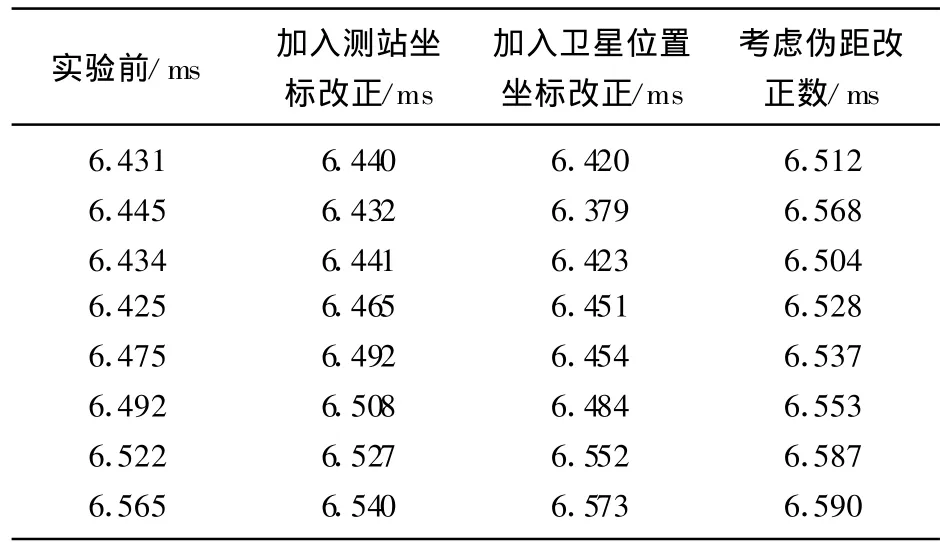
表1 不同误差源对结果的影响

其变化情况如图1、图2和图3所示。

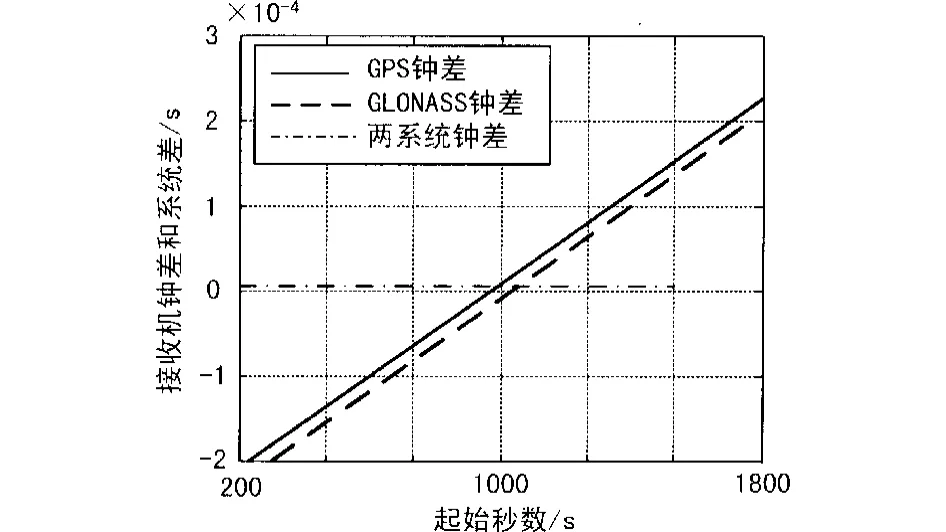
图1 GPS 30号与GLONASS 13号卫星钟差比较

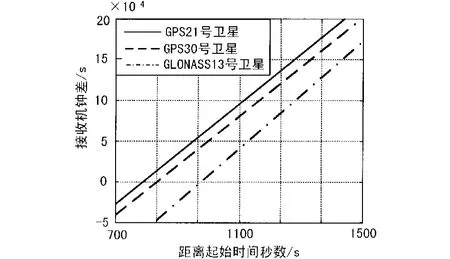
图2 GPS 21、30号和 GLONASS 13号卫星钟差比较

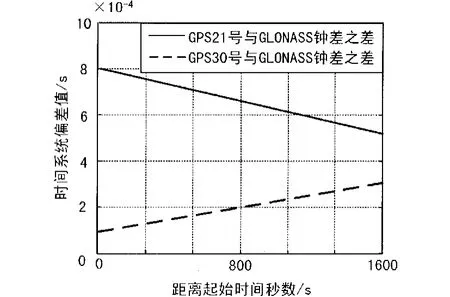
图3 GPS和GLONASS时间系统偏差值

3.3 计算结果

在以上计算中得到的时间系统的差异包含两部分:一部分是与测量、计算相关的可估计的差 δu;一部分是 2 个系统的真正差值 δt,即 δt′=δt+δu。

对可估计的那部分影响予以估值如下:

①已知点位坐标精度对测算精度的影响。已知点的坐标精度在分米级,对结果的影响在10 ns左右;

②卫星位置的影响。IGS精密星历对卫星位置的精度高达厘米级,对结果的影响低于0.1 ns.IGEX精密星历的精度低于米级,对结果的影响在10 ns左右;

③卫星钟差、电离层对流层延迟、多路径效应等等效伪距约10 m,结果变化在100 ns左右。

从以上分析中,可以得出GPS和GLONASS时间系统的差异除了3 h和闰秒外,约有μ s级的差值。

4 结束语

在实际工程应用中,若需要精确测定这些μ s级的具体差值,还应分别对GPS和GLONASS进行长期的观测来把握其随时间变化的规律,并选用相应得平差模型来得到更为精准的相差值,从而大幅提高双模接收机的定位精度,使其测量值更为可靠。该方法可以推广至基于多种卫星导航系统的多模接收机。

[1]J¨ORGEN B¨ORJESSON.GLONASS Contributions to Space Geodesy[J].GNSS Technical Report,2000(2):P35-37.

[2]PETERSON.GPS/GLONASS Time Difference Measurements and Test Bed Development[J].GRA,1995(1):19-21.

[3]BANERJEE P,MATSAKIS D.Time Transfer Through GPS,and the Harmonization of GPS,GLONASS and Galileo for Timing[J].GRA,2007(1):24-28.

[4]李天文.GPS原理及应用[M].北京:科学出版社,2003.