Kalman滤波在天线数字引导跟踪中的应用

刘国栋,李华伟,底 哲,张小龙

(中国电子科技集团公司第五十四研究所,河北石家庄050081)

0 引言

在无人机测控系统中,地面站的定向天线对飞行目标实现实时准确的跟踪是保证测控链路稳定可靠的关键。在天线伺服跟踪系统中,数字引导(简称数引)是重要的跟踪方式之一。数字引导的方法有:①通过惯导或GPS直接提供的飞行目标位置信息解算天线指向的引导方式;②通过高度表获取飞行目标高度并通过测距获取飞行目标距地面站距离解算天线指向的引导方式。不难看出,数字引导包括飞行目标上原始引导信息的获取、原始引导信息无线传输、地面原始引导信息的解算、天伺系统方位和俯仰角度控制执行等4个主要环节。而上述各个环节存在信息传输和处理延时。在跟踪目标大动态飞行,定向天线波束很窄的条件下,数字引导的时滞无法满足应用需求,因此需要对数字引导数据进行实时地外推、预测。

Kalman滤波是对运动目标进行跟踪的一种有效的算法,针对目标跟踪时滞问题,文献[3]采用Kalman一步预测对机动目标跟踪进行外推处理,文献[4]提出组合Kalman隔点预测法进行解决,对观测数据采取隔若干点抽样Kalman处理,等效加大了一步预测间隔。本文针对某测控系统工程实际情况,采取在Kalman滤波处理基础上,对滤波后数据进行平移外推的方法进行多点预测处理,进而解决时滞问题。

1 无人机测控系统数引延时分布

无人机测控系统数引的实现通常是通过将机载上GPS等定位设备提供的位置信息借助无线测控链路传送到地面测控站,测控站上的计算机解算出伺服方位、俯仰角度,经由地面测控通道送达天伺机构控制天线数引跟踪目标完成的。下面对数引信息处理流程各环节中的延时进行分析。

无人机测控系统数引延时分布如图1所示。包括机载上串口接收延时T1和编码调制延时T2;空间无线传输延时T3;地面解调译码延时T4、计算机接收延时T5、数引结算软件计算延时T6、伺服机构串口接收数引数据延时T7和伺服机构天线控制相应延时T8。其中延时T1和T7均是串口总线接收方式,其延时由传输数据帧长和总线传输波特率决定;延时T2和T4包括链路设备内数据编解码、信号调制解调、上下变频带来的延时;空间无线传输延时T3y由传输距离决定,以300 km距离计算,空间传输延时最大1 ms,基本可以忽略;随着计算机CPU运算速度的飞速发展,延时T5和T6相对其他延时基本可以忽略;延时T8由天伺控制机构传输响应函数决定。由此可得总延时为:

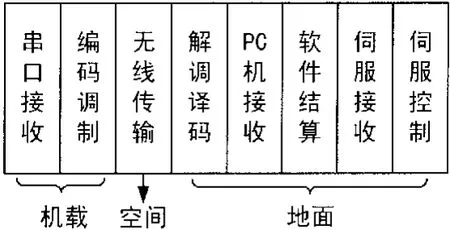
图1 无人机测控系统数引延时分布框图

2 Kalman滤波预测算法

Kalman滤波采用状态空间的概念,把信号过程视为白噪声作用下的线性系统的输出,输入输出关系用状态方程描述;借助信号过程的状态转移方程,根据前一时刻的估计输出量,得出当前时刻的预测估计量,并通过与当前输入量的误差,滤波修正预测估计,输出当前时刻的估计输出量;以这种不断预测-修正的线性递推方式获得逐点滤波结果。下面给出离散线性系统模型的Klaman滤波和实现平移预测的公式及必要的说明。

离散线性系统的n维状态方程和m维测量方程为:

式中,W(k)和 V(k)均值白噪声或高斯白噪声序列;W(k)和 V(k)的自协方差阵分别为 Qkδkj,互协方差阵为0。

状态向量的初始值 X(0)的均值为 μ0,方差为P0。并且,X(0)与 W(k),V(k)互不相关;Qk为非负定阵;Rk为正定阵;P0为非负定协方差阵。

上述系统的Kalman滤波计算公式为:

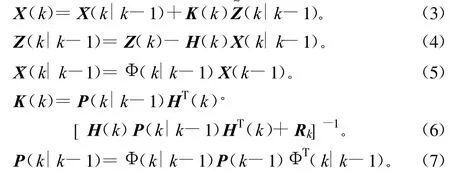
式中,^X(k)为滤波方程;˜Z(k|k-1)为新息方程;^X(k|k-1)为一步预测方程;K(k)为滤波增益阵方程;P(k|k-1)为预测估计误差方差阵;P(k)为滤波估计误差方差阵。只要给出状态变量初值X(0)、P(0),就可由上面公式逐点递推滤波获得状态估计量 ^X(k)。不难理解,^X(k)是经过一步预测,再经过滤波修正后的结果,并遵循最小方差迹的准则。为了实现多点预测,也就是说要将时间间隔适当的放大若干倍,对应一步状态转移矩阵 Φ(k|k-1)将修正为M步状态转移矩阵 Φ(k+M|k-1),在Kalman逐点滤波的同时,在k时刻得到M步预测估计量,其预测方程如下[1]:

3 天线数引跟踪模型

定向天线二维数引目标跟踪的状态变化量为天线的方位角和俯仰角,天线跟随飞行目标运动,可认为是变速运动,方位角(或俯仰角)离散变量可表示为x1(k),角速度离散变量可表示为x2(k),角加速度离散变量可表示为x3(k)。假设在等间隔h上进行测量获得角度数据,在k时刻得到的角度测量数据z(k)表示为[1]:

式中,v(k)为测量噪声且为零均值白噪声序列,方差E[v2(k)]=Rk。当测量时间间隔h很小时,方位角x1(k)可近似为:

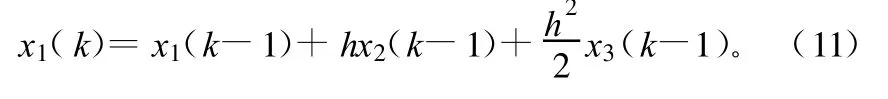
令

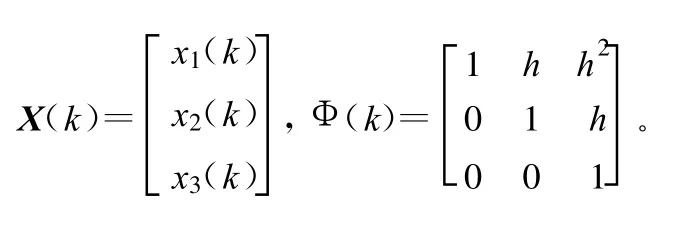
则

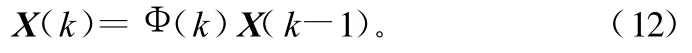
其近似性用对角加速度加以随机干扰进行补偿,所以数引数据的状态的动态方程为:

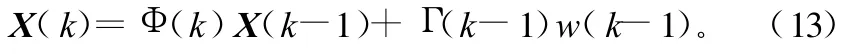
式中,Γ(k)=[0 0 1]T;状态噪声w(k-1)也是零均值白噪声;方差E[w2(k)]=Qk,同时测量方程改写为:

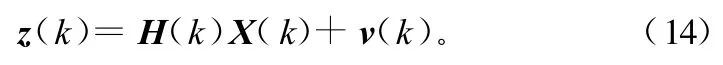
式中,H(k)=[1 0 0]。

这样,就得到天线方位角(或俯仰角)数引跟踪近似的线性时不变系统模型。

4 仿真与应用

4.1 模型仿真

依据上面的天线数引跟踪模型和Kalman滤波外推算法,采用Matlab软件进行仿真验证。工程中天线伺服系统的最大速度为30°/s,最大加速度为15°/s。这里为方便模拟天线转动的角度、角速度以及角加速度,采用正弦信号作为激励源来验证,并对存在和不存在测量噪声2种条件下进行仿真,角度模拟sin正弦信号表达式为:

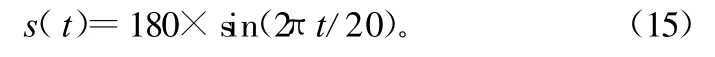
对应角速度和角加速度表达式为:

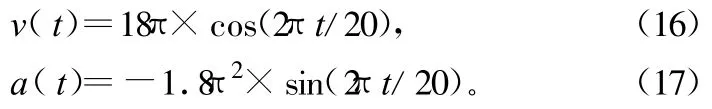
仿真参数大于实际的系统的角速度、加速度要求。输入观测样点时间间隔0.04 s,对滤波预测外推0步,5步、10步进行仿真,初始预测值 X(0)设为0向量,P(0)设为单位阵。在无测量噪声条件下,外推曲线同sin理论曲线对比图如图2(a)所示,并对状态噪声Qk取值1、10、100条件下的预测曲线和sin理论曲线匹配后的误差方差进行了统计,数据如表1所示。在存在测量噪声条件下,外推曲线同sin理论曲线对比图如图2(b)所示,状态噪声Qk取值1、10、100条件下的预测曲线和sin理论曲线匹配后的误差方差统计数据如表2所示。

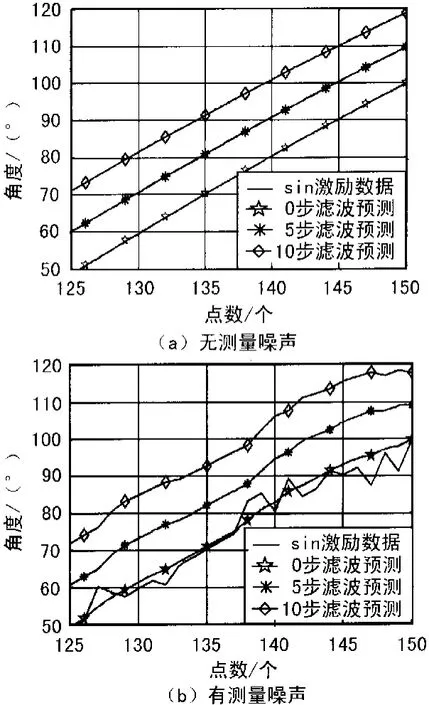
图2 外推曲线同sin理论曲线对比图

表1 外推与理论曲线误差方差统计表(无测量噪声)

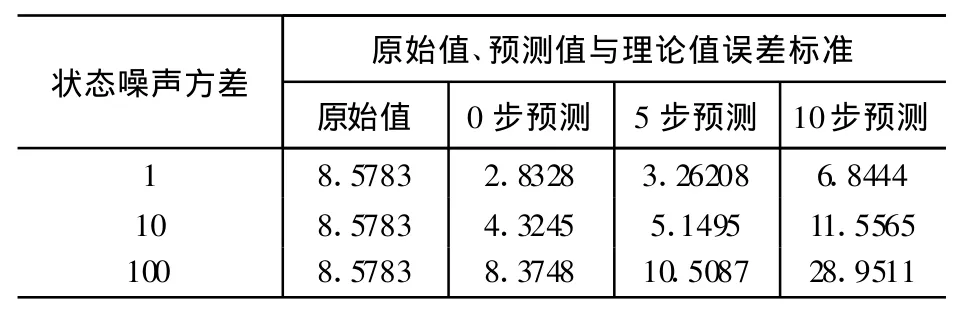
表2 外推与理论曲线误差方差统计表(有测量噪声)

从仿真计算结果可得如下结论:

①在无白噪声和干扰条件下,平滑数引数据进行适当点数的Kalman平移预测外推,外推数据与原始数据误差与状态噪声方差相关,合理调整状态噪声方差,误差可控在较理想范围;外推点数过大,则会引起数据发散;

②在存在白噪声和干扰条件下,Kalman滤波处理(0步预测)对数引数据具有一定的滤波效果;随平移预测外推点数增加,对数引数据的滤波性能逐渐减弱直至振荡发散,误差方差恶化;

③通过合理选取参数,使得设计模型尽可能与实际模型相似,可以实现多点Kalman预测外推,并且具有一定的滤波效果,当原始数据受到干扰越小,外推逼近效果越好。

4.2 工程应用

通过对某测控系统数引数据延时进行链路延时测试,获得数引延时在240 ms左右,数据间隔40 ms,Kalman外推点数为6,对某次目标方位角度数引原始数据和Kalman 6步预测的数据截取一段对比如图3所示。从图中曲线可以看出,通过Kalman 6步预测使得方位角度数引数据得到平移外推;并对数据小幅度波动具有滤波效果,如A点区域;对较大数据断点也有一定平滑效果,如B点区域。

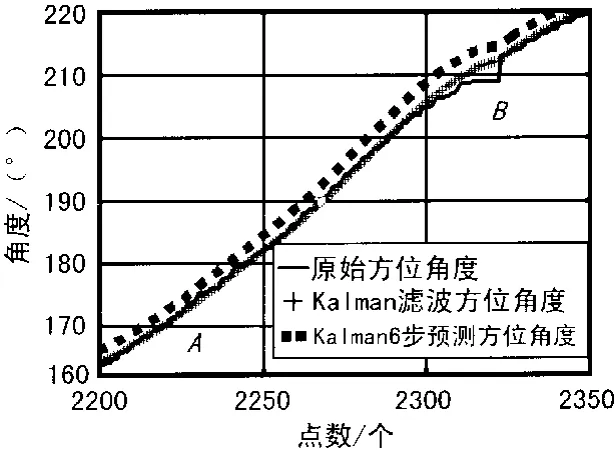
图3 数引方位角度数据曲线图

5 结束语

在上述仿真验证的基础上,对某测控系统天线数引跟踪数据进行Kalman滤波平移预测外推处理,较好地解决了时滞问题。当然,实际获取的数引数据不可避免地存在错数、野值以及多种数据融合带来的数据不连续等问题,仅通过Kalman滤波是无法全面的解决。对此,诸多相关文献[5,6]已进行了大量的研究,并提出许多实际工程解决方案可以采用,只有将这些技术、方法综合起来,才能圆满解决实际工程问题。

[1]刘 豹.现代控制理论[M].北京:机械工业出版社,1983.

[2]王志贤.最优状态估计与系统辨识[M].西安:西北工业大学出版社,2004.

[3]袁洪印,郭丽虹.Kalman预测方法用于跟踪机动目标的仿真研究[J].吉林农业大学学报,2003,25(6):679-681.

[4]袁洪印,郭立红.组合Kalman隔点预测法用于跟踪机动目标的仿真研究[J].光学精密工程,2004,12(2):169-173.

[5]祝转民,杨宜康.Ka lman滤波工程应用问题分析及改进方法研究[J].宇航学报,2002,23(3):44-47.

[6]孙书鹰,段修生.目标跟踪系统中野值的判别与剔除方法[J].火力与指挥控制,2004,29(6):85-87.