动力学在交通事故处理中的应用

孙 伟

（山西省临汾人民警察学校，山西 临汾 041000）

近年来，我国就职业教育进行了大量的投资，职业教育也越来越受到人们的重视，但目前我国职业教育的现状仍有许多不足之处，尤其职业教育特色不明显，缺乏活力和吸引力。现就职业教育教学中的经验谈自己的一点体会。

在公安教育教学中，物理作为一门基础学科，笔者认为它应该处处体现为专业课程的教学服务，更重要的是，在物理教学中，应使基础知识和技能转化为学生的综合素质和科学技能。例如，在交通事故处理当中，常常需要事故处理部门对肇事车辆的行驶速度作出科学的鉴定。对事故车辆碰撞前后的速度分析及推算，实质上就是要最终推算出临近事故，采取措施前的车辆行驶速度。推算这种行驶速度的目的，首先是可以确定该车是否超过了规定速度，因为超速行驶是造成汽车事故的重要原因之一；其次是分析在推算出的速度下，驾驶员是否采取了与这一速度不相适宜的操作方式，从而根据车辆行驶速度的高低确定当事人在交通事故中有无违章行为（超速）存在，为进一步判定对当事人在事故中责任的大小提供准确依据。对肇事车辆行驶速度作出科学的鉴定，不仅是交通专业必需掌握的知识，也是刑事侦察专业必需掌握的知识。在现场勘察中，如何就事故现场的实况，判断肇事车辆的速度，在这里笔者从动力学的角度谈几点看法：

1 转弯过程中的极限度的估算

1.1 不侧滑时的转弯极限速度的估算

车在转弯过程中，汽车的受力情况：见图1，汽车受3个力作用，重力G，方向竖直向下；地面对汽车的支持力N，方向垂直于地面向上，由于汽车向左转弯时，有相对于地面的向右的运动趋势，所以受地面对轮胎向左的水平方向的滑动摩擦力f，为汽车的转弯提供向心力，即指向圆心的方向。

图1 汽车的受力情况

假设汽车在水平路面上做匀速圆周运动，则重力G和支持力N，大小相等，方向相反，彼此平衡，物体所受的合力等于水平方向所受到的滑动摩擦力f，即合力F合=f，设路面和轮胎间的摩擦系数M是一定的，又因为N=G，由摩擦力的概念可知f=μG，因此f是一定的，即F合是恒定的。

要保证车辆在转弯过程中不至发生侧滑，则车辆的线速度与路面提供的向心力必须满足：

由公式可见，滑动摩擦系数和转弯半径越小，则转弯的极限速度越低。式中摩擦系数为固定常数，可通过实验测定，关于弯道半径可用如下的简易方法测量，见图2，在弯道的路沿或路中线上截取一段圆弧，测量其弦长AC和弦高BD，设圆弧的半径为R，由图可知：

R2=（AB2+（R-BD2））

图2 弯道半径的测量

所以，利用上式可估算出转弯过程中不侧滑时的转弯极限速度。

1.2 转弯时有横向正坡度的转弯及速度的估算

见图3，在弯道有横向坡度时，且为正坡度，此时车辆向左转弯，临界速度时，车辆受重力G，支持力N，同时车辆有相对于斜面斜向上的运动趋势，所以还受沿斜面斜向下的摩擦力f。

由于车辆竖直方向的加速度为零，则在竖直方向的合力为零，水平方向的合力F合为车辆的转弯提供向心力，于是:

图3 转弯时有横向正坡度

由（1）（2）得：

F向=F合=

将（4）代入（3）得：

在临界速度时，车辆的线速度和向心力满足如下关系：

整理得：

此为曲率半径与极限转弯速度的关系。

1.3 转弯时有横向负坡度的转弯极限速度的估算

见图4，当弯道有负坡度时，此时车辆向右转弯，临界速度时，车辆有沿斜面斜向下的运动趋势，故车辆受斜向上的摩擦力f，同正坡度时相比较，此时车辆在竖直方向的合力为零，水平方向的合力为车辆的转弯提供向心加速度，则有：

图4 转弯时有横向负坡度

由①②得：

将（4）代入（3）得：

F向=F合=

则在临界速度时，车辆的线速度和向心力之间满足如下关系：

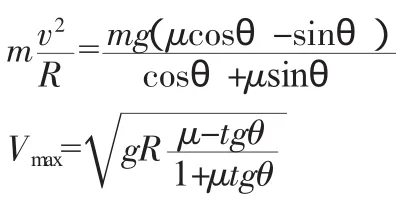
整理得：

此为曲率半径与极限转弯速度的关系。

可见，在横向坡度为正坡度时，极限转弯速度，要比没有横向坡度的道路大；横向坡度为负值时，极限转弯速度，比没有横向坡度的道路小。

2 不倾翻时的最大极限转弯速度的估算

2.1 水平路面上不倾翻的最大极限转弯速度的估算

假设车辆与路面相对静止，且车辆与路面一起绕弯道曲率的圆心作圆周运动，取路面为非惯性系，则在非惯性系中，车辆处于静止状态，则此时车辆受重力G，地面对轮的支持力 NA、NB，及惯性力 F，地面对轮的滑动摩擦力 fa、fB，当汽车处于不倾翻时的最大极限速度时，NA等于零。

图5 水平路面的转弯速度的估算

设两轮间距离为b，重心高度为h，则不倾翻时汽车绕B轮在竖直平面内顺时针转动，由力矩的平衡条件及力矩的概念可知，此时重力G与轮间距b的一半，及惯性力F与重心高h所构成的一对力矩相对平衡，其余力矩力矩均为零，即:

惯性离心力矩：

M1=-Fh=-mh

重力力矩：

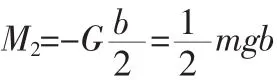
所以有:M1+M2=0

即:

整理得:Vmax=

此为临界状态时，汽车不倾翻的最大极限速度。

2.2 横向坡度为正坡度时，不倾翻的最大极限转弯速度的估算

假设斜路面与车辆一起绕弯道曲率的圆心作向左的圆周运动，取斜路面为非惯性系，在非惯性参照系中，车辆处于静止状态，见图6则车辆受重力G，地面对轮的支持力NA、NB，地面对轮的静摩擦力fa、fB以及惯性力的作用F。

图6 正坡度时转弯速度的估算

设汽车处于不倾翻时的最大极限速度，则车辆相对于非惯性系绕支点B轮转动，此时NA、NB、fa、fB所产生的力矩均为零，且车辆处于平衡状态，所以重力矩和惯性离心力矩的代数和为零，则重力和惯性离心力正交分解，其所产生的力矩分别为：

重力力矩：

惯性离心力矩：

由力矩的平衡条件，汽车最大极限速度，即临界状态时满足：

MG+MF=0，即：

整理得：

即：

此时的速度，即为横向正坡度时，汽车不倾翻的最大极限速度。

图7 负坡度时转变速度的估算

2.3 横向坡度为负坡度时，不倾翻的最大极限转弯速度的估算

见图7，假设倾斜路面与车辆一起绕弯道曲率的圆心作向右的匀速圆周运动，取倾斜路面为非惯性系，则倾斜路面为非惯性参照系，车辆处于静止状态，汽车受到重力G，地面对轮的支持力NA、NB，地面对轮的静摩擦力fa、fB，以及惯性离心力F的作用。

汽车处于不倾翻时的最大极限速度时，车辆相对于非惯性系绕支点A轮在竖直平面内转动，同上述正坡度相比较，此时NA、fa、fB所产生的力矩为零，NB等于零，即这部分力所产生的力矩不作考虑，所以重力矩和惯性离心力矩的代数和为零，同理将重力和惯性离心力正交分解，其所产生的力矩于是有：

重力力矩：MG=

由转动平衡的条件可知，汽车最大极限速度，即临界状态时满足：MG+MF= 0，即：

这就是横向负坡度时，汽车不倾翻的最大极限转弯速度。

由此可见，在横向坡度为正坡度时，不倾翻时的最大极限转弯速度，要比没有横向坡度时的速度大。反之，若横向坡度为负坡度时，其不倾翻时的最大转弯速度比没有横向坡的水平道路的速度小。

综上所述，测量出汽车转弯过程中的曲率半径和路面与轮胎间的摩擦系数，即可求出汽车转弯过程中不侧滑时的转弯极限速度；测量出汽车的重心高度及轮间距，还可求出转弯过程中不倾翻时的最大极限转弯速度。