有理函数模型在光学卫星影像几何纠正中的应用

2010-06-11祝小勇唐新明

航天返回与遥感 2010年4期

关键词：检查点控制点光学

张过李扬祝小勇唐新明

(1武汉大学测绘遥感信息工程国家重点实验室,武汉430079)

(2湖北省环境科学研究院环境规划研究所,武汉430072)

(3国家测绘局卫星测绘应用中心,北京100830)

1 引言

随着航天科技的发展,我国资源卫星和遥感卫星陆续发射升空,国内测绘卫星数据应用越来越广泛。国产光学卫星如“资源一号”、“资源二号”和“遥感二号”等都已稳定在轨运行。虽然国产光学卫星影像分辨率在不断提高,但影像的几何定位精度仍然较低,这在一定程度上影响了影像的有效利用,造成卫星资源的巨大浪费。因此,研究提高国产光学卫星影像的几何定位精度的方法具有重要意义。

“资源二号”卫星(ZY-2)是推扫式光学遥感卫星,其全色影像空间分辨率为3m,面幅为30km×30km,主要用于国土资源勘查、环境监测与保护、城市规划、农作物估产、防灾减灾和空间科学实验等领域。“遥感二号”卫星也是推扫式光学卫星,其全色影像空间分辨率为2m,面幅为24km×24km,主要用于科学实验、国土资源普查、农作物估产和防灾减灾等领域[1]。

线阵推扫式光学传感器是逐行以时序方式获得二维卫星影像。首先,在像面上形成一条线图像;然后,卫星沿着预先设定的轨道向前推进,逐条扫描后形成一幅二维影像。影像上每行像元在同一时刻都以中心投影的方式成像,所以整个影像为多中心投影[2-3]。为了对这种新型传感器遥感影像进行几何处理,必须重建三维立体模型并进行测量工作。原有的基于多项式拟合和共线条件方程的遥感影像几何纠正和定位方法已经无法准确表达推扫式传感器的成像本质了,必须建立成像几何模型,也称成像数学模型。目前,国外光学卫星都普遍采用严密成像几何模型或其他通用成像几何模型对影像进行几何处理。

有理函数模型(Rational Function Model,RFM)是一种通用成像几何模型,它具有良好的内插特性和连续性并独立于传感器和平台之外。本文分析了国产光学卫星影像的严密成像几何模型和RFM,并对“资源二号”和“遥感二号”影像做了几何纠正试验。

2 国产光学卫星影像的严密成像几何模型

所谓成像几何模型,是指建立影像点(x,y)和地面点(XD,YD,ZD)之间的数学关系[4]。对任何一个传感器成像过程的描述都可以通过一系列点的坐标来进行。建立推扫式光学严密成像几何模型需要利用坐标系之间的转换,最后将影像坐标与地面坐标联系起来,这种关联就构成了模型的正反算。

对于国产光学卫星,利用GPS测定GPS相位中心的位置,利用星敏感器测定星敏本体在J2000坐标系下的指向。为了得到相机后节点的位置和相机光轴的姿态,需将GPS和星敏感器测定的数据转换为相机后节点的位置和相机光轴的指向。因此在不考虑大气折射影响的条件下,可以构建国产高分辨率光学遥感影像的严密几何成像模型[5-6]:

文献[2]对模型误差进行了详细分析。从中可知,卫星遥感影像几何纠正的理论精度为:在沿轨道方向主要受到星历数据、时间误差、俯仰角和航偏角等因素的影响;在垂直轨道方向主要受到星历数据、滚动角、侧视角、时间误差等因素的影响;在轨道面上受到星历数据、姿态、侧视角、时间误差等因素的影响。

3 国产光学卫星影像的有理函数模型

有理函数模型将地面点大地坐标D(经度Longitude,纬度Latitude,高程Height)与其对应的像点坐标d(行Line,列Sample)用比值多项式关联起来。为了增强参数求解的稳定性,将地面坐标和影像坐标标准化到-1～1之间。对于一个遥感影像,可定义为比值多项式[7]:

式中 NL(P,L,H),DL(P,L,H),NS(P,L,H),DS(P,L,H)为P,L,H的三次多项式;(P,L,H)为正则化的大地坐标经度、纬度、高程;(X,Y)为正则化的影像像素坐标。

研究表明,在有理函数模型中,光学投影系统产生的误差可以用有理多项式中的一次项表示,地球曲率、大气折射和镜头畸变等产生的误差能用有理多项式中的二次项进行模型化,其他一些未知的具有高阶分量的误差如相机振动等,可以用有理多项式中的三次项表示[3]。

3.1 求解有理函数模型参数算法

为了将有理函数模型中参数的求解转换为线性方程,将式(1)变形为

则误差方程为:

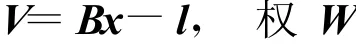
其中

式中 ai,bj,ci,dj(i=1,2,3…,20;j=2,3,4…,20)为式(1)中分子分母三次多项式的系数;W为权矩阵,在有理函数模型参数求解中,一般为单位权矩阵,在形成法方程时省略。根据最小二乘平差原理,可将误差方程变换为法方程,即

本文采用王新洲教授提出的谱修正迭代法求解法方程[8],不论法方程呈良态、病态或秩亏,其运算程序都不需要任何变化。当法方程呈良态时,经几次迭代就可以收敛到精确解;当法方程呈病态时,收敛速度稍慢,但估计结果无偏。具体表述为:

设有(BTWB)x=BTWl,两边同时加 x,得到

其中 E为和BTWB同阶的单位矩阵。

通过对公式(4)迭代求解,获得无偏的x。

3.2 求解有理函数模型参数的流程

有理函数模型参数求解有与地形无关和与地形相关2种方式。在严密成像几何模型已知的情况下,可采用与地形无关的求解方式。用严密成像几何模型建立地面点的立体空间格网和影像面之间的对应关系作为控制点,来求解有理函数模型参数。该方法不需要详细的地面控制信息,仅仅需要该影像覆盖地区的最大高程和最小高程,所以称之为与地形无关的求解方法[7,9]。

与地形无关的方法求解有理函数模型参数的流程可以概括为:首先,根据影像的覆盖范围,利用美国地质调查局提供的全球1km分辨率DEM(Global 30-arc-second Digital EvaluationModel),计算该影像覆盖区域的最大和最小椭球高;其次,在高程方向以一定的间隔分层,在平面上,以一定的格网大小建立地面规则格网,生成控制点地面坐标;再次,利用影像严密成像几何模型的反变换模型,计算控制点的影像坐标;然后,加密控制格网和层,建立独立检查点;进而,利用控制点坐标计算影像坐标和地面坐标的归一化参数,将控制点和检查点坐标归一化;最后,采用谱修正迭代法,求解有理函数模型从而可以获得影像的有理函数模型参数,并用检查点进行检查。

4 几何纠正试验

国产光学卫星影像几何纠正的基本流程为:严密模型建立—有理函数模型参数求解—精化有理函数模型—像元灰度值重采样—精度检查。具体描述如下:

首先,建立影像的严密成像几何模型;其次,利用严密成像几何模型建立地面点立体空间格网和影像面之间的对应关系作为控制点求解有理函数模型参数;再次,依据影像面上的仿射变换关系[10-11],通过少量的地面控制点计算变换参数,以提高有理函数模型精度,在上述过程中要用到相应地区正射影像图和DEM作为参考数据;然后,采用双线性内插法对像元灰度值进行重采样;最后,待几何纠正完成后,在纠正影像和参考影像上对比选取一定数量的同名检查点,比较它们的坐标来验证纠正精度。

下面依据上述方法分别对两景“资源二号”卫星影像(平原和山区)和一景“遥感二号”卫星影像进行几何纠正试验。“资源二号”影像的地面分辨率为3m,可以满足1∶50 000的测绘制图需求;“遥感二号”影像的地面分辨率为2m,可以满足1∶25 000的测绘制图需求。因此采用1∶10 000的DEM和DOM作为控制数据是合理可行的。试验中选取的控制点误差均在1个像元以内,且符合分布均匀,密周边布点原则。

4.1 “资源二号”平原地区影像几何纠正试验

试验数据为“资源二号”卫星影像,对应地区为北京城区,影像标称分辨率3m,影像大小为10 002×10 000像元。首先,利用本文提出的方法求解该景影像有理函数模型参数;其次,利用北京地区1∶10 000正射影像图选取了一定数量的控制点对有理函数模型进行精化;最后,采用对应地区1∶10 000DEM对试验影像进行正射纠正。

为了评价纠正精度,试验在纠正影像和参考正射影像上分别对比选取了8个同名检查点,比较坐标差值并计算中误差。中误差为观测值与真值偏差的平方与观测次数比值的平方根,在几何纠正中,观测值就是纠正结果点位的坐标值,真值为对应的参考正射影像的坐标值。“资源二号”北京城区影像几何纠正控制点与检查点分布如图1所示,具体纠正精度见表1。

图1 “资源二号”北京城区影像几何纠正控制点与检查点分布

表1 “资源二号”北京城区影像几何纠正精度表m

4.2 “资源二号”山区影像几何纠正试验

试验数据为“资源二号”卫星影像,对应地区为北京山区,影像标称分辨率3m,影像大小为10 002×10 000像元。首先,利用本文提出的方法求解该景影像有理函数模型参数;然后,利用北京地区1∶10 000正射影像图选取了一定数量的控制点对有理函数模型进行精化;最后采用对应地区1∶10 000DEM对试验影像进行正射纠正。

为了评价纠正精度,与4.1节试验相同,在纠正影像和参考正射影像上分别对比选取了8个同名检查点,比较坐标差值并计算中误差。“资源二号”北京山区影像几何纠正控制点与检查点分布如图2所示,具体纠正精度见表2。

图2 “资源二号”北京山区影像几何纠正控制点与检查点分布

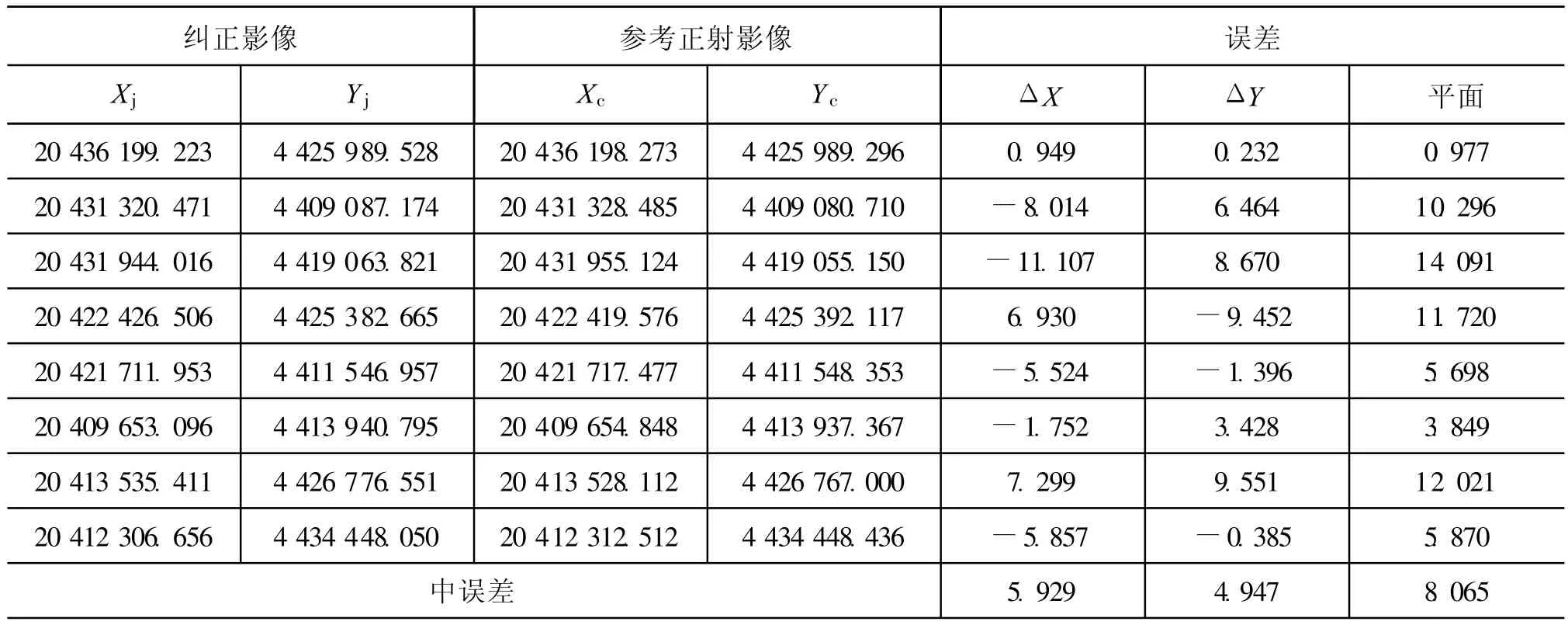
表2 “资源二号”北京山区影像几何纠正精度表m

4.3 “遥感二号”台湾地区影像几何纠正试验

试验数据为“遥感二号”卫星影像,对应地区为台湾地区,影像标称分辨率2m,影像大小为12 271×12 000像元。首先,利用本文提出的方法求解该景影像的有理函数模型参数;其次,利用台湾地区1∶10 000正射影像图选取了一定数量的控制点,对有理函数模型进行精化;最后,采用对应地区1∶10 000DEM对试验影像进行正射纠正。

为了评价纠正精度,试验同样在纠正影像和参考正射影像上分别对比选取了8个同名检查点,比较坐标差值并计算中误差。“遥感二号”台湾地区影像几何纠正控制点与检查点分布如图3所示,具体纠正精度见表3。

图3 “遥感二号”台湾地区影像几何纠正控制点与检查点分布

表3 “遥感二号”台湾地区影像几何纠正精度表m

5 结束语

4.1 节试验和4.2节试验分别针对“资源二号”平原和山区2种影像进行了几何纠正,从试验结果来看,平原影像纠正精度达到2个像元以内,山区达到3个像元以内。4.3节试验对“遥感二号”台湾地区一景影像进行了几何纠正,从试验结果来看,纠正精度达到了3个像元以内。上述试验所用的控制数据均为1∶10 000的正射影像和DEM。从文献[1]中可以了解到,采用同等精度的控制数据,国外光学卫星,如SPOT-5影像的纠正精度能达到1个像元以内,IKONOS影像纠正精度能到1个像元左右。

通过分析上述试验结果可以得到以下结论:

1)有理函数模型能正确拟合严密成像几何模型对国产光学卫星影像进行几何处理工作。

2)虽然国产光学卫星的空间分辨率在逐步提高,但几何定位精度仍无法与国外光学卫星相比,这说明国产光学卫星在内检校工作方面依然不够完善。

[1]孙承志,唐新明,翟亮.我国测绘卫星的发展思路和应用展望[J].测绘科学,2009,34(2):5-7.

[2]张过.缺少控制点的高分辨率卫星遥感影像几何纠正[D].武汉:武汉大学,2005.

[3]张永生,巩丹超,刘军,等.高分辨率遥感卫星应用[M].北京:科学出版社,2004

[4]孙家柄.遥感原理与应用[M].武汉:武汉大学出版社,2003.

[5]袁修孝,张过.缺少控制点的卫星遥感对地目标定位[J].武汉大学学报(信息科学版),2003,28(5):505-509.

[6]江万寿,张剑清,张祖勋.三线阵CCD卫星影像的模拟研究[J].武汉大学学报(信息科学版),2002,27(4):414-419.

[7]祝小勇,张过,秦绪文.国产光学卫星影像RPC制作[J].国土资源遥感,2009,2:32-34.

[8]王新洲,陶丰藻,邱卫守,等.高等测量平差[M].北京:测绘出版社,2006.

[9]巩丹超,张永生.有理函数模型的解算与应用[J].测绘学院学报,2003,20(1):39-42.