基于HHT边际谱熵和能量谱熵的心率变异信号的分析方法
2010-06-09董红生邱天爽张爱华郝晓弘
董红生 邱天爽 张爱华 郝晓弘
1(兰州理工大学电信学院,兰州 730050)
2(兰州工业高等专科学校电气工程系,兰州 730050)
3(大连理工大学电信学院,大连 116024)
引言
心率变异(heart rate variability,HRV)是指人体心脏搏动周期存在的微小变异,通常情况下是指连续心跳间RR间期的微小涨落,其信号包含了有关心血管系统神经及体液调节的大量信息。大量研究表明自主神经系统(交感神经和副交感神经)与心率变异性之间存在着重要的联系[1]。因此,HRV分析常被用来作为判断自主神经活动的非侵入性指标,在评价心血管系统功能和预测心血管疾病突发方面有重要意义[2]。传统的HRV分析包括线性时域和频域分析方法,其分析理论成熟、算法简单,已有商业仪器应用于临床和医学实验中[3-5]。心率波动易受到如运动、呼吸、血压、体温及情绪等诸多因素的影响,还会受到微小干扰(如心室早收缩等)的影响,这些都使得HRV信号表现出高度的非平稳性和复杂性,普遍认为HRV信号是混沌的或是含有混沌成分的信号,并不能用线性方法完全解释[6]。基于非线性动力学方法的HRV信号研究引起了国内外学者的关注,非线性方法主要包括Lyapunov指数、分数维、测度熵以及多种复杂性测度等[7-10],其中复杂性测度在生物医学信号分析中取得的成果尤其引起了广泛的关注[11-14]。
熵的概念源于热力学(热力学熵),1984年Shannon将熵的概念引入信息论,定义了信息熵(香农熵)作为某事件的不确定性测度。虽然香农熵是针对信息论提出的,但其具有广义熵的意义,被广泛用来表征信号的信息量和复杂性。在信号处理领域中,认为信号越不规则,熵值越高;信号越规则,熵值越低;信号完全规则时,熵值为零。常用的测度熵,如 Kolmogrov-Sinai(KS)熵,是通过计算新信息的平均产生率来表征信号的复杂性;近似熵(ApEn)则来源于KS熵,适用于短时序列复杂性分析;而样本熵(SampEn)是对近似熵的修正。近年来,关于熵的研究一直是国内外研究的热点,但主要集中于时域熵,如近似熵、样本熵[15-19]。与时域分析表示相比,信号的频域表示往往更能体现信号的本质特征[20],功率谱熵就是基于频域的熵分析方法,在频域上表示了信号的不确定性,但其理论依据仍是傅里叶(FT)变换,因此在分析非线性、非平稳信号信号时(如HRV),不可避免地会出现某些缺陷,如虚假频率问题。Huang等提出了一种全新的信号分析方法——希尔伯特-黄变换(HHT),创造性地提出固有模式函数(IMF)为组成信号的基本信号,并给出了经验模式分解(EMD)、Hilbert谱和边际谱等新概念。理论上,HHT能精确给出信号中频率随时间变化的规律,避免虚假频率等冗余现象,对于处理非线性、非平稳信号有清晰的物理意义,能够得到信号的振幅-时间-频率分布特征,且具有自适应性[21-23]。
本研究基于 HHT理论,依据广义信息熵的定义,提出基于HHT边际谱熵和能量谱熵的概念,以及基于上述熵的HRV信号分析方法。对几种常规信号进行复杂性分析,仿真结果表明,本方法和常用的信号复杂度分析方法有相同的结论,且更好地反映信号复杂程度的变化。利用Logistic映射进入混沌后的87个序列,在每个序列加入随机脉冲干扰,评价了本方法的抗干扰性能,仿真结果表明,本方法对噪声较为敏感,但性能好于多值粗粒化的LZ复杂度和功率谱熵的方法。对MIT-BIH标准数据库中健康年轻人、健康老年人及房颤病人的HRV信号仿真分析表明,本方法对于HRV信号复杂度分析十分有效,明显地区分了3组HRV信号,统计学性能优于传统的功率谱熵的方法。
1 原理
1.1 经验模式分解
HHT包含两个过程:经验模态分解(EMD)和Hilbert变换。EMD的目的是通过对非线性、非平稳信号的分解,获得一系列表征信号特征时间尺度的固有模态函数(IMF),使得各个IMF分量为窄带信号,以便进行Hilbert变换。IMF分量必须满足两个条件:一是在整个数据集中,其极值点的个数和零交叉点的个数相同或至多相差一个点;二是在时间序列的任意时刻,其极大值点和极小值点构成的上下包络线的均值为零。
通过EMD分解,任何复杂信号都可以表示为有限个IMF之和,即有
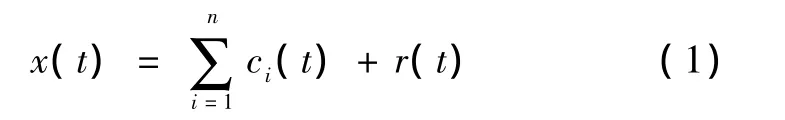
式中:ci(t)(i=1,…,n)为 n个 IMF模态分量,r(t)为残差(或趋势项)。
在实际计算中,必须确定一定的误差准则使EMD过程能够中止,一般是利用两个连续处理结果之间的标准差SD作为判据,SD的取值在0.2~0.3之间为宜,既保证IMF分量的线性稳定性,又使IMF分量具有相应的物理意义。
1.2 Hilbert变换和Hilbert谱分析
设c(t)是实信号 x(t)的一个 IMF分量,做Hilbert变换得
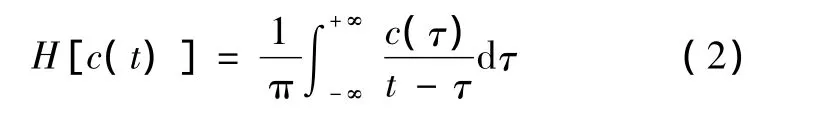
Hilbert变换可以在不造成信息损失的前提下,将一个实信号构造成一个复信号(解析信号),记生成的解析信号为z(t),则有
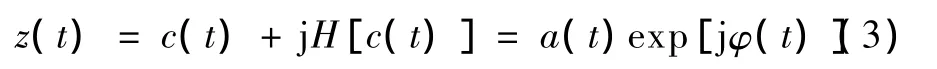
其中,幅值 a(t)和相位φ(t)分别为
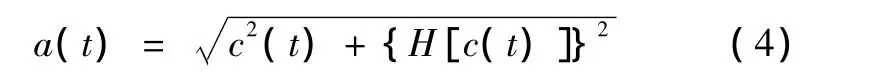
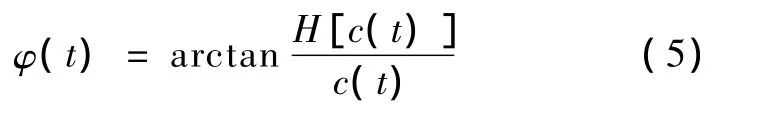
由瞬时相位可求得c(t)的瞬时频率为
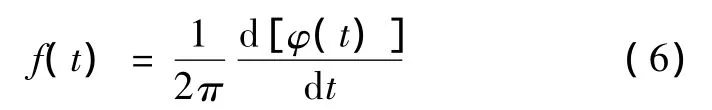
对式(1)的每个 IMF分别应用Hilbert变换,则信号x(t)可表示为
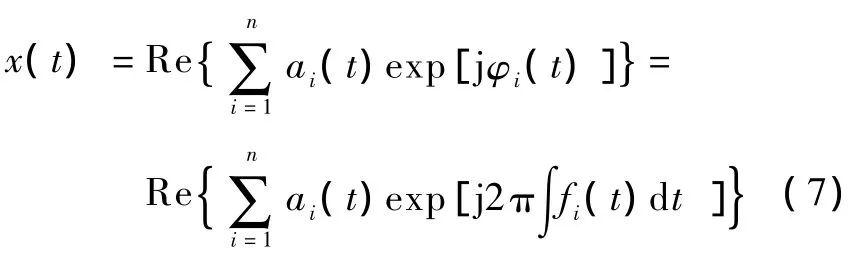
式中,Re表示取实部,n为IMF分量个数,省略了残差函数r(t)。
由式(4)、式(6)可以看出,由 Hilbert变换得到的幅值和频率都是时间的函数,故可将信号幅度在三维空间中表示成时间和频率的函数 H(f,t),称之为Hilbert幅值谱,即

H(f,t)精确地描述了信号的幅值随时间和频率的变化规律。将H(f,t)对时间积分,即可得 Hilbert边际谱,有
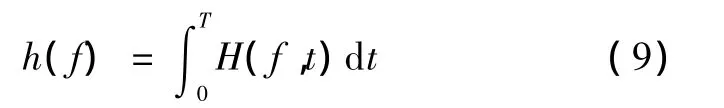
边际谱提供了对每个频率的幅值量测,表示在整个时间长度内统计意义下的幅值累积。将幅值的平方对时间积分,还可得到Hilbert能量谱,即
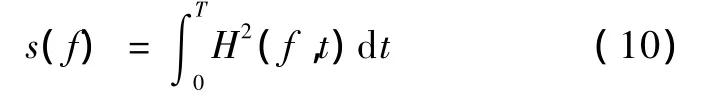
Hilbert能量谱是对于每个频率的能量量测,表示在整个时间长度内每个频率所累积的能量。
1.3 HHT边际谱熵和HHT能量谱熵
信息熵是从平均意义上描述信源的总体特征的,表征了信源的平均不确定性,也可看作对系统信息量的不确定性量测。信息熵越大,表示信号的平均信息量越大,信号的不确定性越大,即信号越复杂。
在离散的频率点f(kΔf),有

式中,n是信号在分析频带内的频率离散点数。
按照信息熵定义,给出HHT边际谱熵为
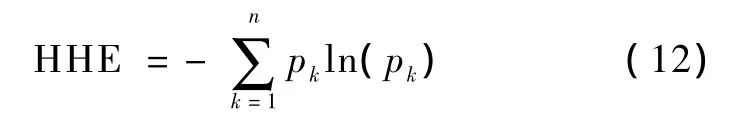
其中,pk=h(k)/∑h(k),表示第k个频率对应幅值出现的概率。熵值归一化为0~1,则有

式中,N是h(k)序列长度。
同理,可以定义HHT能量谱熵,用来描述HHT能量谱的不确定性。HHT能量谱熵为:
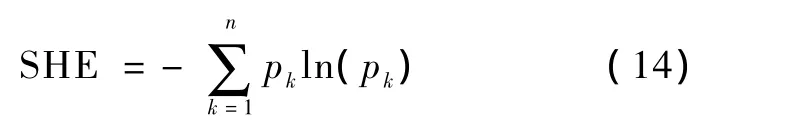
式中,pk=s(k)/∑s(k),表示第k个HHT能量谱在整个谱中所占的百分比。熵值归一化为0~1,则有

式中,N是s(k)序列长度。
HHT边际谱熵和能量谱熵表示信号在频域上的不确定性,可作为信号复杂性的一种度量,刻画了时间序列的谱结构情况。信号的幅值(能量)在整个频率成分上分布越均匀、信号越复杂,不确定性程度也就越大。
2 实验方法
2.1 基于HHT边际谱熵和能量谱熵的常规信号分析
为了考察HHT边际谱熵和能量谱熵对不同随机程度信号的识别能力,选取如下具有不同随机程度的常规信号序列(序列长度N=3 000)进行复杂性计算[24]:
1)正弦信号y=sin(10x),采样间隔为10 ms;
2)正弦信号与白噪声信号的混合序列,y=y1+qy2,其中y1为正弦序列,y2为白噪声序列,q为随机成分的混入比例,分别取q=0.2,0.5,0.7;
3)实高斯白噪声序列;
4)利用Lorenz映射方程,得到Lorenz信号。
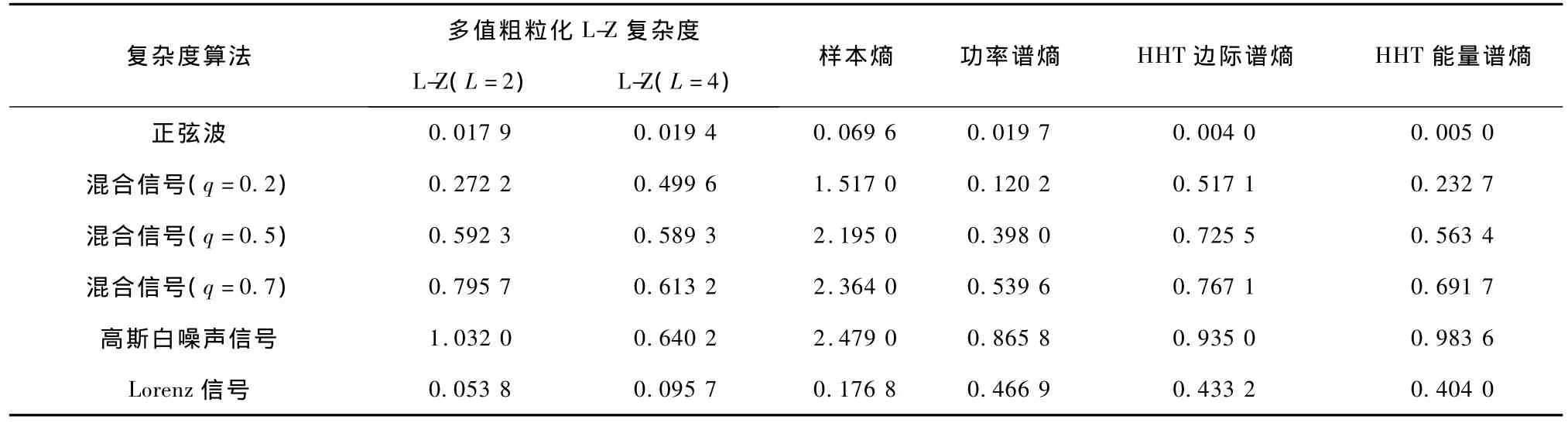
上述常规信号序列波形(数据长度截取1 000点)如图1所示。对每种信号分别用Lempel-Ziv复杂度、样本熵、功率谱熵、HHT边际谱熵和能量谱熵计算其复杂度,其中Lempel-Ziv复杂度分别采用2符号和4符号多值粗粒化方法,样本熵中取嵌入维m=2,矢量匹配容差 r=0.15SD(SD为序列标准差)。通过对几种常规信号的测试,可以说明HHT边际谱熵和能量谱熵对具有不同复杂程度信号的识别能力及效果。
2.2 HHT边际谱熵和能量谱熵的抗干扰性能分析
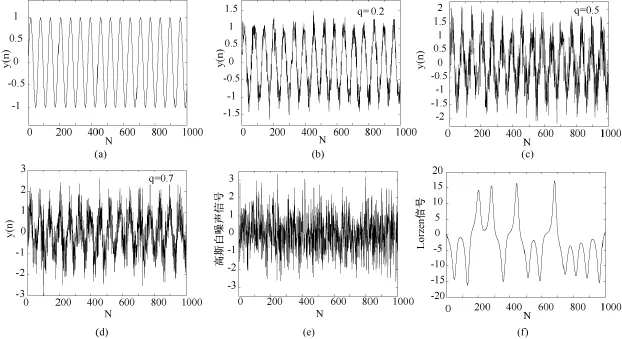
图1 几种常规信号。(a)正弦信号序列;(b)混合序列(q=0.2);(c)混合序列(q=0.5);(d)混合序列(q=0.7);(e)实高斯白噪声序列;(f)Lorenz信号序列Fig.1 Several conventional signals.(a)sine signal sequence;(b)mixing sequence(q=0.2);(c)mixing sequence(q=0.5);(d)mixing sequence(q=0.7);(e)real Gaussian white noise sequence;(f)Lorenz signal sequence
在实际非线性时间序列(如心率变异 HRV、脑电信号等)中,常常存在一些脉冲干扰,这些干扰数据会很大程度地影响复杂度和熵值的计算。
考虑Logistic映射,它随时间的演化是一个典型的非线性动力学系统,其方程为

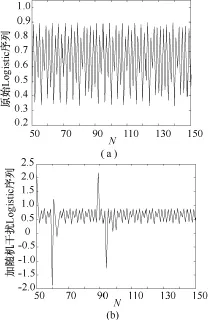
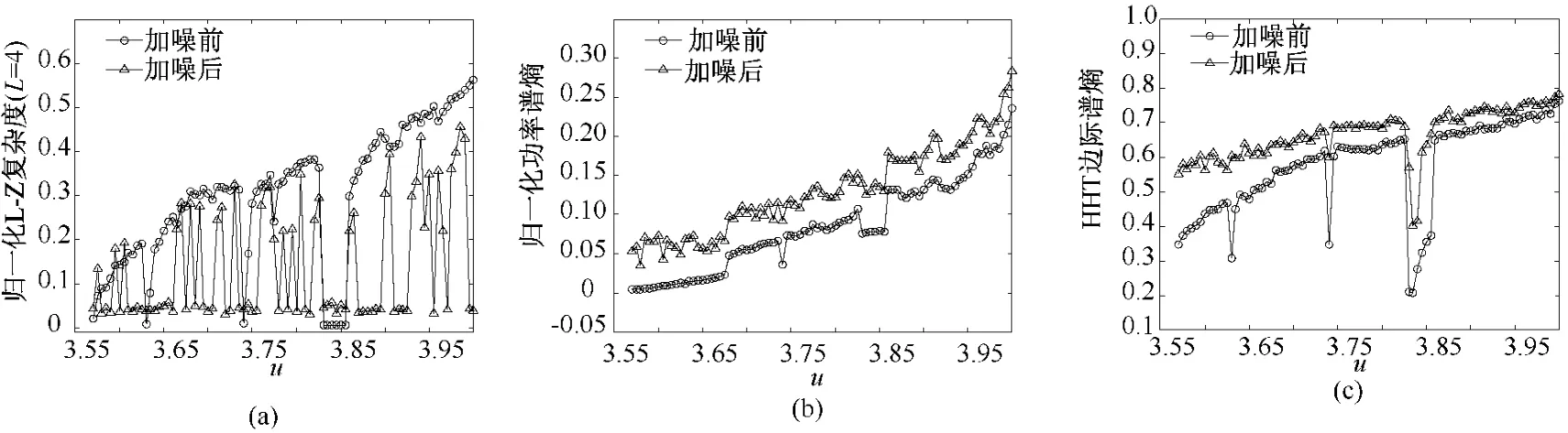
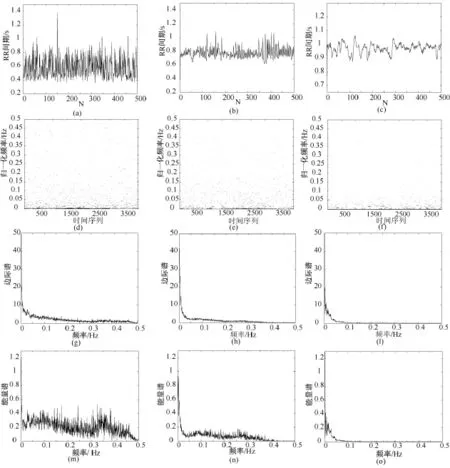
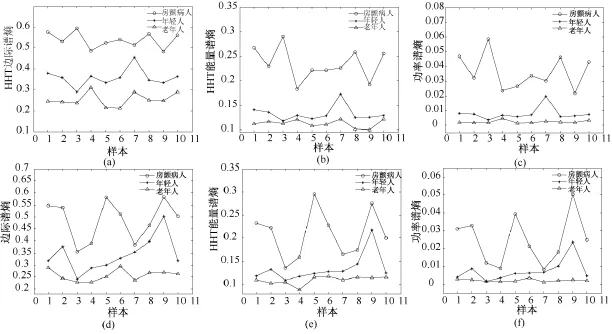
式中,x(i)∈[0,1],u 为控制参数,当 3.569 实验数据取自Logistic映射进入混沌后的87个序列,序列长度N=3 000,均去掉了前100次迭代的数据,控制参数 u=3.57~4.00,步长0.005。按文献[13]的方法随机加入强脉冲干扰信号,随机干扰信号的幅值大小为±3,相对于Logistic序列数值的大小是很强的脉冲干扰。加噪前后的波形如图2所示(截取了第5个序列的100个数据点)。分别利用多值粗粒化的L-Z方法、功率谱熵方法及HHT边际谱熵和能量谱熵方法,计算87个序列加噪前后的复杂度和熵值。 为了度量干扰对复杂度和熵值大小的影响,以加噪前的复杂度序列为参考序列,定义加噪后复杂度序列的相对变异系数为 式中,C0为参考序列的复杂度和熵,C1为加噪序列的复杂度和熵,n为复杂度序列的长度。 图2 Logistic序列加随机强干扰前后的波形。(a)原始序列;(b)加随机干扰序列Fig.2 Logistic sequence and Logistic sequence with random strong interference. (a)the original sequence;(b)adding random interference 通过对抗脉冲干扰性能的分析,可以反映本方法对实际的生物医学信号分析的稳定性。 从MIT-BIH心电数据库中,取20名健康年轻人、20名健康老年人和20名房颤病人的HRV信号为测试信号。20名健康年轻人(21~34岁)和20名健康老年人(68~85岁)的HRV信号取自 MITBIH的Fantasia Database(简称FD数据库),分为f1y(01~10)、f1o(01~10)和 f2y(01~10)、f2o(01~10)两组。10名房颤病人的HRV信号取自 MITBIH的 The MIT-BIH Atrial Fibrillation Database(简称MBAF数据库),另外10名房颤病人的 HRV信号取自The Long-Term AF Database(简称LTAF数据库)。HRV信号的数据长度均取为 N=3 000点,随机在MBAF数据库中抽取10名房颤病人,和FD数据库的f1y(01~10)、f1o(01~10)构成一个实验对象组;随机在LTAF数据库中抽取10名房颤病人,和FD数据库的 f2y(01~10)、f2o(01~10)构成另一个实验对象组。分别计算两个实验组HHT边际谱熵和能量谱熵,并与功率谱熵做对比。 几种常规信号的复杂度和熵值的归一化计算结果如表1所示。可以看出,几种描述信号复杂度的方法的计算结果是一致的:周期正弦信号的复杂度最低,完全随机的高斯白噪声的复杂度最高;混合信号根据其随机成分的增加复杂度逐步增大,介于正弦信号和高斯白噪声之间;Lorenz信号的Lempel-Ziv复杂度和样本熵高于周期正弦信号而低于混合信号,其功率谱熵和混合信号(q=0.5、0.7)接近;HHT边际谱熵及能量谱熵低于混合信号,且有较大差异,更好地区别了信号复杂性程度。 表1 几种常规信号的复杂度计算结果Tab.1 The complexity of the several conventional signal 多值粗粒化的L-Z方法、功率谱熵方法及HHT边际谱熵方法在序列加噪前后的复杂度和熵值变化如图3所示。可以看出,加噪前3种方法均能较好地反映信号复杂度的变化,加噪后L-Z复杂度方法受干扰的影响很严重,不能反映信号复杂度的变化情况。功率谱熵和HHT边际谱熵在加噪后熵值有一定增加,但仍能表征信号复杂度变化趋势。 表2是几种方法的复杂度和熵值的相对变异系数v,分析可知,HHT边际谱熵和能量谱熵抗扰性能要好于功率谱熵和L-Z复杂度方法。必须指出,基于频域的熵分析方法的抗干扰能力有限,对于存在强脉冲干扰的信号序列必须对信号进行一定的预处理,方可获得较好的性能。 图3 Logistic序列加噪前后复杂度和熵变化。(a)加噪前后L-Z复杂度变化;(b)加噪前后功率谱熵变化;(c)加噪前后HHT边际谱熵变化Fig.3 The complexity and entropy of Logistic sequence before and after adding noise.(a)L-Z complexity change;(b)power spectrum entropy change;(c)HHT marginal spectrum entropy change 表2 加噪前后复杂度和熵序列的相对变异系数Tab.2 Relative variation coefficient of complexity and entropy before and after adding noise 图4 HRV信号、Hilbert谱、Hilbert边际谱及 Hilbert能量谱。(a)~(c)房颤病人/年轻人/老年人的HRV信号;(d)~(f)房颤病人/年轻人/老年人的 Hilbert谱;(g)~(l)房颤病人/年轻人/老年人的Hilbert边际谱;(m)~(o)房颤病人/年轻人/老年人的Hilbert能量谱Fig.4 HRV signal,Hilbert spectrum,Hilbert marginal spectrum and Hilbert energy spectrum.(a~c)The HRV signal of patient with atrial fibrillation,young and elder;(d~f)The Hilbert spectrum of patient with atrial fibrillation,young and elder;(g~l)The Hilbert marginal spectrum of patient with atrial fibrillation,young and elder;(m ~o)The Hilbert energy spectrum of patient with atrial fibrillation,young and elder 在实验组中取一组数据,绘制年轻人、老年人和房颤病人的 HRV信号、Hilbert谱、Hilbert边际谱及Hilbert能量谱,如图4所示。从 Hilbert谱、边际谱和能量谱图中,可以看到年轻人、老年人和房颤病人的幅度(能量)随频率分布的情况,HRV信号的大部分幅值(能量)分布在极低频和超低频范围,房颤病人在整个频率范围内都有幅值(能量)的分布,年轻人在频率大于0.4 Hz后几乎没有幅值(能量)分布,而老年人在频率大于0.1 Hz后也几乎没有幅值(能量)分布。因此,从频域角度看,房颤病人的HRV信号最为复杂,年轻人的HRV信号复杂性高于老年人,这与人体神经自律能力随年龄老化而逐渐下降,导致其对心脏的控制能力下降、心脏电活动的混沌程度降低的观点是一致的。房颤病人的HRV信号有较大复杂性,其隐含的生理意义有待深入研究。可见,Hilbert谱、Hilbert边际谱及 Hilbert能量谱不但给出了HRV信号的能量分布,也从频域角度定性地刻画了HRV信号的复杂度。 利用HHT边际谱熵和能量谱熵方法评价三类HRV信号的复杂性,并与功率谱熵方法进行比较。两个实验组的熵值计算结果如图5所示,其中(a)~(c)为第一实验组的HHT边际谱熵和能量谱熵及功率谱熵的计算结果,(d)~(f)为第二实验组的计算结果。可以看出,两组实验对象三种熵值的变化趋势基本一致,说明本研究的熵分析方法是可行的,而且HHT边际谱熵在区分房颤病人、年轻人和老年人的性能方面明显好于HHT能量谱熵和功率谱熵。 将两实验组合并进行统计分析,使用均值±标准差对各参数进行描述,实验对象的熵均值及统计分析如表3所示。实验对象的3种熵值组间进行双边t检验,在工程技术检验中,一般显著水平α取为0.001。当显著性概率 P<α(0.001)时,认为组间存在统计学上的显著性差异,P值越小,组间的差异越明显。实验对象的双边 t检验结果见表3注,结果显.3种熵分析方法的显著性概率P均远小于0.001,说明3组对象之间存在显著差异。比较组间显著性概率P的大小,可以看出:HHT边际谱熵显著性概率 P最小,HHT能量谱熵次之,因此,HHT边际谱熵的区分性能最优,HHT能量谱熵好于功率谱熵的性能。实际数据分析表明,两种新的熵分析方法在频域上量度信号的不确定性更加清晰,可以作为信号复杂性的一种有效的度量方法。由于本方法能有效地区分房颤病人和健康人,说明不仅可以用于评价老年化对于HRV信号的影响,而且可以用于临床疾病的辅助诊断,其分析性能优于常用的功率谱熵分析方法。 图5 两组实验对象HHT边际谱熵、能量谱熵及功率谱熵。(a)~(c)第一实验组熵;(d)~(f)第二实验组熵Fig.5 HHT marginal spectral entropy and energy spectrum entropy and power spectral entropy for two groups of the experimental sample.(a~c)The first group entropy;(d~f)The second group entropy 心率变异性(HRV)分析作为一种间接评价心脏自主神经功能的分析方法,具有无创性、敏感度高和可定量的优点,在心血管系统功能评价和突发性心血管疾病预测方面有重要的临床医学研究价值。对于非线性、非平稳性的HRV信号分析,传统的线性分析方法有一定的局限性。HHT是一种新的具有自适应的时频分析方法,它可根据信号的局部时变特征进行自适应的时频分解,具有很高的时频分辨率和良好的时频聚集性,非常适合于非平稳、非线性信号的分析。熵分析方法被广泛用来表征信号的复杂性,通过信号复杂度指标的刻画,有利于揭示一些非线性、非平稳信号的本质特征。 表3 三组对象HHT边际谱熵、能量谱熵和功率谱熵的均值及统计(均值±标准差)Tab.3 The mean of HHT marginal spectral entropy,energy spectrum entropy and power spectral entropy for three groups of sample(mean±SD) 本研究在HHT理论的基础上,结合非线性熵分析方法,提出基于HHT边际谱熵和能量谱熵的信号分析方法,从表1给出的几种常规信号的分析结果来看,HHT边际谱熵和能量谱熵在区分信号复杂性上优于其他方法。从表2反映的Logistic混沌映射序列加噪前后熵值的相对变异系数来看,HHT边际谱熵和能量谱熵的抗扰性能要好于L-Z复杂度和功率谱熵。需要指出的是,对于有强噪声干扰的信号,其抗扰能力有限,要获得好的分析效果,需要进行一定的数据预处理。图5直观地显示了HHT边际谱熵和能量谱熵应用于MIT-BIH标准数据库中实际HRV信号的分析结果,可以看出其熵值的变化趋势和功率谱熵相同,对于年轻人、老年人和房颤病人的区分度非常显著。表3所反映的统计特性表明,其区分性能优于功率谱熵的方法,同时注意到功率谱熵的大小较前两者小很多。从几种熵的计算方法上易推算这一结论,也可从几种熵的物理意义上得到解释。HHT边际谱熵及能量谱熵是基于信号的HHT边际谱和能量谱定义的,而功率谱熵是基于功率谱定义的,在应用于非平稳的HRV信号分析时,功率谱、HHT边际谱和能量谱所反映的信号能量(幅值)的频域分布特性大致相同,但功率谱中的频率(Fourier频率)和HHT边际谱(能量谱)中的频率(瞬时频率)有本质的区别。Fourier频率是用整个正弦或余弦信号定义,而瞬时频率却是一个局部性概念,HHT边际谱(能量谱)的实际含义是信号中瞬时频率的总幅值(总能量)大小。文献[22]的研究表明,HHT边际谱(能量谱)能更准确地反映信号幅值(能量)在频域上的真实分布。这样,对于以边际谱(能量谱)作为信号频域的一种划分而定义熵运算时,各对应谱在整个谱中占的百分比较大(与功率谱熵运算相比),依据广义信息熵的定义所计算的熵值较大,这一结论也可从本研究中几种常规信号的熵值分析直观地看出。总之,实际HRV信号分析的有效性表明,本方法在充分发掘蕴含在HRV信号中的生理病理信息及临床医学的应用,有一定的实际意义。 [1]Clifford GD,Azuaje F,McSharry PE.Advanced methods and tools for ECG data analysis[M].London:Artech House,2006. [2]Malik M.Heart rate variability:standards of measurement,physiological interpretation and clinical use [J].Circulation,1996,93(5):1043-1065. [3]Mietus JE,Peng CK,Henry I,et al.The pNNx files:re-examining a widely used heart rate variability measure [J].Heart,2002,88(4):378-380. [4]Serrador JM,Finlayson HC,Hughson RL.Physical activity is a major contributor to the ultra low frequency components of heart rate variability[J].Heart,1999,82(e9):547 -555. [5]中华心血管病杂志编委会心率变异性对策专题组.心率变异性检测临床应用的建议[J].中华心血管病杂志,1998,26(4):253-255. [6]Clifford GD,McSharry PE.Generating 24-hour ECG,BP and respiratory signals with realistic linear and nonlinear clinical characteristics using a nonlinear model[J]. Computers in Cardiology,2004,31:709 -712. [7]Bogaert C,Beckers F,Ramaekers D,et al.Analysis of heart rate variability with correlation dimension method in a normal population and in heart transplant patients[J].Autonomic Neuroscience,2001,90(1):142-147. [8]Bian CH,Ning XB.Evaluating age-related loss of nonlinearity degree in short-term heartbeat series by optimum modeling dimension[J]. PhysicaA:StatisticalMechanicsand its Applications,2004,337(1-2):149-153. [9]Ivanov PC,Amaral LAN,Goldberger AL,et al.Multifractality in human heartbeat dynamics[J].Nature,1999,399(3):461-465. [10]李锦,宁新宝.短时心率变异性信号的基本尺度熵分析[J].科学通报,2005,50(14):1438-1441. [11]Costa M,Goldberger AL,Peng CK.Multiscale entropy analysis of biological signals[J].Physical Review,2005,71(2):1539-3755. [12]Xu Lisheng,Zhang David,Wang Kuanquan et al.Arrhythmic pulses detection using Lempel-Ziv complexity analysis[J],EURASIP Journalon Applied SignalProcessing,Article ID18268,2006:1 -12. [13]张佃中.Lempel-Ziv复杂度算法中粗粒化方法分析及改进[J].计算物理,2008,25(4):499 -504. [14]白冬梅,邱天爽,鲍海平.基于经验模式分解与样本熵的癫痫预测方法[J].中国生物医学工程学报,2006,25(5):527-531. [15]Lewis MJ,Short AL Sample entropy of electrocardiographic RR and QT time-series data during rest and exercise[J].Physiol Meas,2007,28(6):731-744. [16]Costa M, Golderger AL, Peng CK.Multiscaleentropyto distinguish physiologic and synthetic RR time series [J].Computers in Cardiology,2002,29:137-140. [17]杨福生,廖旺才.近似熵:一种适于短数据的复杂性度量[J].中国医疗器械杂志,1997,21(5):283 -286. [18]Lake DE,Richman JS,Griffin MP,et al.Sample entropy analysis of neonatal heart rate variability[J].Am J Physiol Regul Integr Comp Physiol,2002,283(3):789-797. [19]庄建军,宁新宝,都思丹,等.过速型室性心律失常事件的短时非线性心率变异性预测[J].科学通报,2008,53(5):520-527. [20]Qian Shie,Chen Dapang.Joint time-frequency analysis[J].IEEE Signal Processing Magazine,1999,16(2):52-67. [21]Huang NE,Shen Zheng,Long SR,et al.The empirical mode decompo-sition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proceedings of Royal Society,1998,454:903 -995. [22]钟佑明,秦树人,汤宝平.希尔伯特-黄变换中边际谱的研究[J].系统工程与电子技术,2004,26(9):1323 -1326. [23]陈涛,李正媛,陈志遥,等.Hilbert-Huang变换在固体潮分析中的应用[J].大地测量与地球动力学,2009,29(4):131-139. [24]金宁德,董芳,赵舒.气液两相流电导波动信号复杂性测度分析及其流型表征[J].物理学报,2007,56(2):720-729.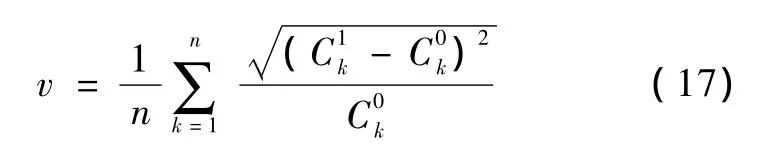
2.3 基于HHT边际谱熵和能量谱熵HRV信号分析
3 结果
3.1 几种常规信号的分析结果
3.2 抗干扰性能的分析结果

3.2 HRV信号的分析结果
4 讨论和结论

