奶牛9分制体型线性评分数据的正态性分析
2010-06-09李培娟安永福2王继华刘松柏
李培娟,安永福2,,王继华,刘松柏
(1.河北工程大学农学院,河北 邯郸 056002;2.河北省畜牧兽医研究所,河北 保定 071000;3.华中农业大学动物科技学院,湖北 武汉430070)
近年来通过体型线性鉴定选择高产、具有标准体型的奶牛群已成为各国的研究重点。鉴于体型的重要性,国内外关于体型性状对产奶性能、繁殖性能、健康性能、终身效益等影响的研究[1~6]也越来越多,这为奶牛的选种选配提供了依据。正态分布是一个重要的连续型随机变量的概率分布。生物现象中有许多变量是服从或近似服从正态分布的,如家畜的体长、体重、产奶量等[7]。奶牛的体型性状作为连续型随机变量,研究其转化为9分制后的数据分布具有一定的意义。
1 材料与方法
1.1 数据来源
本研究的数据来自2006~2007年间对华中某牧场处于1~5个泌乳期、1~11个泌乳月的971头奶牛进行体型线性鉴定的记录。所评定的23个主要性状分别为体高、前段、体躯大小、胸宽、体深、腰强度、尻角度、尻宽、蹄角度、蹄踵深度、骨质地、后肢侧视、后肢后视、乳房深度、乳房质地、悬韧带、前乳房附着、前乳头位置、乳头长度、后乳房附着高度、后乳房宽度、后乳头位置、棱角性[1]。
1.2 数据的测定
按照《中国荷斯坦牛体型线性鉴定规程》(2006)的要求,采用9分制评定方法,对23个线性性状和40个缺陷性状进行线性鉴定[3]。
1.3 数据的整理
利用SPSS16.0软件及FORTRAN90语言自编程序,对23个体型性状转化为9分制评分后的数据进行平均数和方差分析,检验其正态性。
2 结果与分析
2.1 标准差区间的频率检验
通过对23个线性体型性状的9分制体型评分数据进行整理,得出各性状平均值在1~3个标准差区间的次数与频率值,结果见表1。
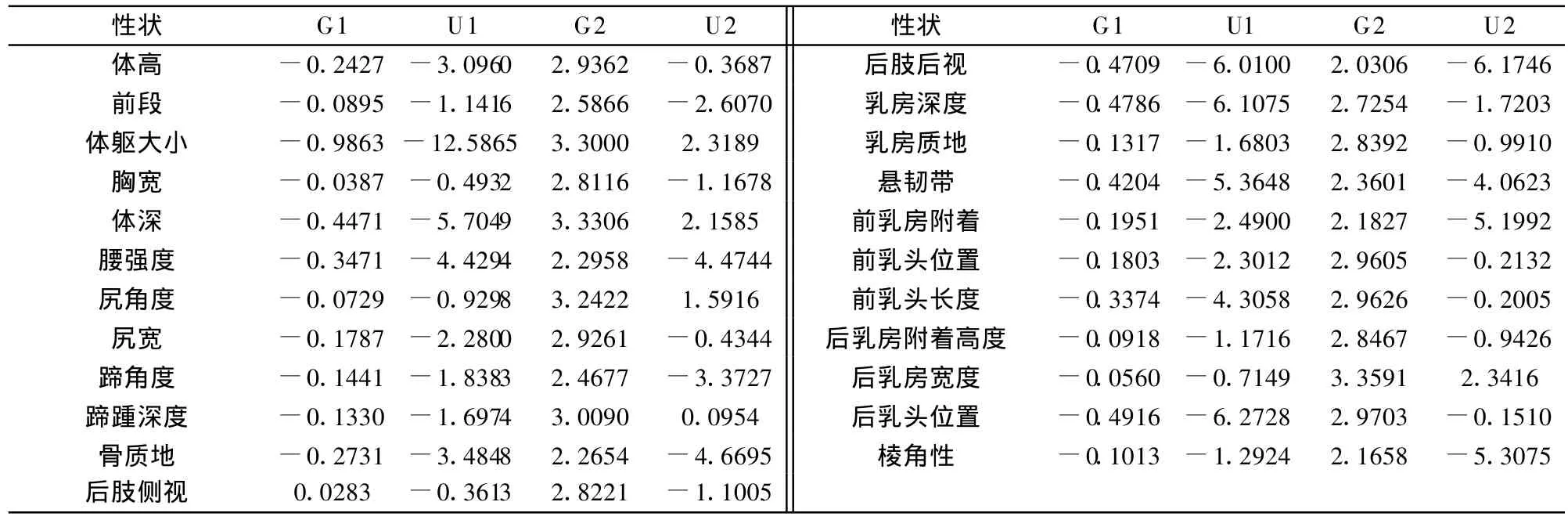
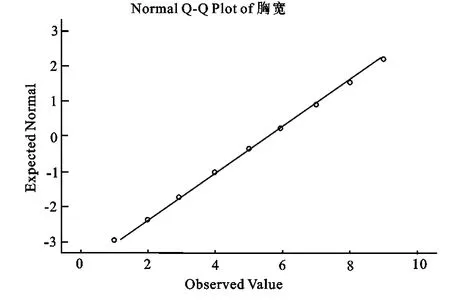
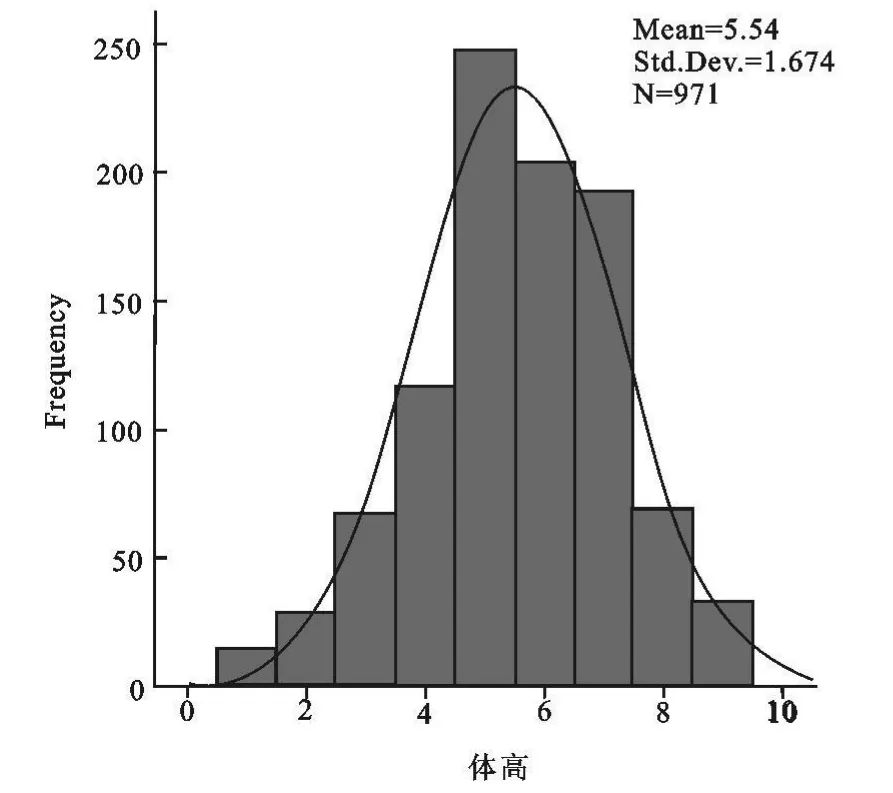
服从正态分布的连续型随机变量[7],在 X±KS的区间上,应该符合这样的概率值:P( X-1S≤X 矩法正态性检验又称偏度峰度检验,是应用随机变量X的标准化变量的三阶矩和四阶矩作为样本偏度(G1)和样本峰度(G2)的检验。 若总体X为正态分布,则可证明当样本含量n足够大时,近似地有[9]:G1~N(0,C1);G2~N(T2,C2)。 其中:C1=6(n-2)/[(n+1)(n+3)];C2=24n(n-2)(n-3)/[(n-1)2(n+3)(n+5)];T2=3-6/(n+1);U1=G1/C1;U2=(G2-T2)/C2 当X为正态分布且n足够大时,近似有U1~N(0,1),U2~ N(0,1)。根据 U检验原理,当 U1、U2的绝对值均小于U0.05时,则接受正态性的假设;否则拒绝。根据上述原理,用FORTRAN 90语言编写程序,计算23个性状的G1,G2,U1,U2(表2),C1,C2,T2值,结果如下: C1=0.0784;C2=0.1562;T2=2.9938。由表2可以看出,服从 1)标准正态分布(U1,U2绝对值都小于U0.05)的性状有:胸宽、尻角度、蹄踵深度、后肢侧视、乳房质地、后乳房高度。 2)正态平阔峰(U2小于0,U2绝对值大于U0.05)的性状有:前段、蹄角度、后乳房附着高度。 3)负偏态正峰(U1小于0,U1绝对值大于U0.05)的性状有:体高、尻宽、乳房深度、前乳头位置、后乳头位置。 4)不服从正态分布(U1,U2绝对值都大于U0.05)的性状有:体躯大小、体深、腰强度、骨质地、后肢后视、悬韧带、前乳房附着。 该结论与1.1检验最接近正态分布的性状和偏离正态分布的性状的结论,除了骨质地有较大差距外,其余基本一致。 表1 23个体型性状9分制评分数据的标准差区间的频率检验 正态Q-Q图检验是根据散点落在给定斜线周围程度来判断样本是否符合正态分布的检验。若大部分点落在斜线周围则表明服从正态分布;否则不服从。按照2.2检验结果,在4种结果中各选取1个代表性状(胸宽、前段、体高、体躯大小)作为例子图:图中横坐标为性状观测值,纵坐标为正态期望值。从图1~图4可以看到:图1~图3多数数据都集中分布在斜线周围,表明这些性状的分布基本近似服从正态;图4绝大多数点偏离斜线,表明该类性状分布不服从正态。 表2 23个体型性状9分制评分数据的矩法检验表 图1 胸宽Q-Q概率正态检验图 图2 前段Q-Q概率正态检验图 图3 体高Q-Q概率正态检验图 图4 体躯大小Q-Q概率正态检验图 例子图所选性状同上:图中横坐标为性状观测值,纵坐标为频率值。图中右上角标明了该性状的平均值(MEAN)、标准差(STD.DEV)、样本含量(N)等统计量。从图5~图8可以看到:图5~图7代表的性状分布基本近似服从正态分布,图8代表的性状明显不服从正态分布。 标准差区间的频率检验定量的分析出前段、胸宽、尻角度、蹄踵深度、骨质地这几个性状值最接近标准正态分布给定区间的概率值;体躯大小、体深、腰强度、后肢后视、前乳房附着值相对偏离。矩法检验结果与标准差区间的频率检验结果除了骨质地外,均一致。Q-Q概率图检验、直方图模拟的正态分布曲线检验,符合正态与不符合正态分布的性状与上面两种方法(2.1,2.2)的结果一致,但是根据矩法正态性检验得到的符合正态平阔峰和负偏态正峰里的体高、尻宽两性状也近似服从正态分布。乳房深度、前乳头位置、前乳头长度、后乳头位置4种检验结果均是负偏态正峰分布。 图5 胸宽直方图 图6 前段直方图 图7 体高直方图 图8 体躯大小直方图 综合上述分析,本次试验结果可得出如下结论: 而且,这与刘松柏(2008)[8]的结论,武汉荷斯坦牛体型具有尻部理想、四肢强健的优点恰好一致。说明该地区奶牛的这些性状不仅服从正态分布而且发育优秀,可以根据它进行选配以改良其它地区奶牛的该性状。 体高、尻宽等性状虽然矩法正态性检验检验方法证明这些性状呈现负偏态,但是根据Q-Q图和直方图来看,这些性状也近似服从正态分布。造成这种结果的原因可能是地理因素,为适应南方炎热高湿的环境[1],所以体型偏小;另外,据程郁昕等(2005)[10]研究表明:体高随胎次升高有下降趋势。 造成这种结果的原因初步分析主要有以下几点:①鉴定员评定误差;②抽样误差;③检验方法;④体型评分的9分制转化问题;⑤测定年、季节、胎次及管理因素。这些性状在刘松柏(2009)[8]分析中都不是理想性状,这可能也与该性状的分布没有达到正态有关。这也给我们提供了一个用性状的分布来检测性状是否理想的依据。 造成这种结果的原因初步分析原因同上3。另外体躯大小的性状是由胸围估测体重,由于体重受到体高、胸围、胸宽等多种因素的影响,仅由胸围来估测体重,可能有一定的误差;而体深、腰强度等性状主要由鉴定员判定为准,可能也会造成一定的误差。 鉴于有多种因素对奶牛9分制体型评分后数据有影响,所以对于奶牛体型评分转换为9分制后的分布问题还有待进一步研究。奶牛体型性状经9分制评分后,数据仍然多数近似服从正态分布,可以从这一事实出发,完善现行奶牛的体型评分制度,为奶牛育种的全面发展提供参考。 [1]刘松柏.武汉地区荷斯坦牛体型线性性状的遗传分析[D].湖北.华中农业大学,2008. [2]师守堃,刘仲贤等.奶牛体型线性评定[M].中国奶协,1990,7-10. [3]De Groot B J,Keown J F,Van Vleck L D,et al.Genetic Parameters and Responses of Linear Type,Yield Traits,and Somatic Cell Scores to Divergent Selection for Predicted Transmitting Ability for Type in Holsteins[J].J Dairy Sci,2002,85:1578-1585. [4]Sewalem A,Kistemaker G J,Miglior F,et al.Analysis of the Relationship Between Type Traits and Functional Survival in Canadian Holsteins Using a Weibull Proportional Hazards Model[J].J Dairy Sci,2004,87:3938-946. [5]Sewalem A,Kistemaker G J,Van Doormaal B J,et al.Relationship Between Type Traits and Longevity in Canadian Jerseys and Ayrshires Using a Weibull Proportional Hazards Model[J].J Dairy Sci,2005,88:1552-1560. [6]Dal Zotto R,De Marchi M,Dalvit C,et al.Heritabilities and Genetic Correlations of Body Condition Score and Calving Interval with Yield,Somatic Cell Score,and Linear Type Traits in Brown Swiss Cattle[J].J Dairy Sci,2007,90:5737-5743. [7]明道绪主编.生物统计附试验设计[M].北京:中国农业出版社,2001,45-46. [8]刘松柏,易建明,晏邦富,等.武汉地区荷斯坦牛体型性状的遗传参数估计[J].湖北农业科学,2009,7(43):1690-1693 [9]盛 骤,谢式千,潘承毅.概率论与数理统计[M].第四版.北京高等教育出版社,2008,206-208. [10]程郁昕,方必春,高士宝,等.淮南地区荷斯坦奶牛15个一级体型性状的线性评定[J].中国奶牛,2005,5:19-22.2.2 矩法正态性检验

2.3 正态Q-Q概率图检验
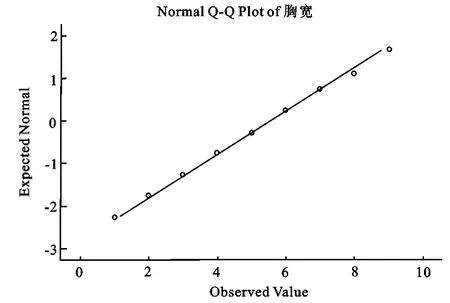


2.4 直方图模拟正态分布检验
3 讨论与小结

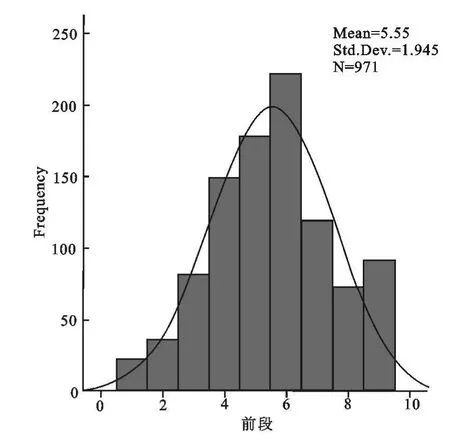

3.1 前段、乳房深度、尻角度、胸宽、后肢侧视等性状符合正态分布
3.2 体高、尻宽等性状近似服从正态分布
3.3 乳房深度、前乳头位置、前乳头长度、后乳头位置等性状经检验为负偏态正峰
3.4 体躯大小、体深、腰强度、悬韧带、后乳房附着高度等性状不服从正态分布
