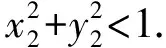谈高考数学试题对运算能力的考查

● (宁波万里国际学校中学 浙江宁波 315040)

高考《考试大纲》中明确指出运算能力的要求是：会根据法则与公式进行正确运算、变形和处理数据；能根据问题的条件，寻找与设计合理、简捷的运算途径；能根据要求对数据进行估计和近似计算. 本文对此举例分析，供考生复习时参考.

1 运算要准确

运算准确是运算的第一要求.

例1若向量a⊥b，且a⊥c，d=λb+μc(λ,μ∈R,λμ≠0)，判断向量a与d

( )

A.a⊥dB.a∥d

C.a=dD.a∥d或a⊥d

错解由a⊥b，且a⊥c，得

a·b=0,且a·c=0，

于是

a·d=a·(λb+μc)=λ(a·b)+μ(a·c)=

λ×0+μ×0=0，

得a⊥d.故选A.

分析由a·d=0，可得a=0或d=0或a⊥d,并不一定能够得到a⊥d. 因此，上面的解答是错误的，即当a与b都是非零向量时，

a⊥b⟺a·b=0.

正解由a⊥b，且a⊥c知a≠0，于是：

(1)当d≠0时，由a·d=0，得a⊥d；

(2)当d=0时，由规定知a∥d.

综合(1)，(2),得a∥d或a⊥d.

故选D.

点评在解答计算型问题时，运算要准确，这是第一要求，务必要牢记，这也是最低要求.

2 运算要合理

运算合理是运算的第二要求.

例2已知函数f(x)是定义在[-1,1]上的增函数，且同时满足：

①f(x)是奇函数；

②对任意的a,b∈[-1,1]，且a+b≠0，都有

(1)试判断函数f(x)的单调性，并给予证明；

(2)若f(1)=1，且不等式f(x)≤m2-2bm+1对所有的x∈[-1,1],b∈[-1,1]恒成立,求实数m的取值范围.

解(1)设-1≤x1

即

f(x1)

故f(x)在[-1,1]上是增函数.

(2)由f(1)=1，得

f(x)max=f(1)=1.

若f(x)≤m2-2bm+1对所有的x∈[-1,1],b∈[-1,1]恒成立,则

f(x)max≤m2-2bm+1,

即

1≤m2-2bm+1,

得

m2-2bm≥0.

(1)

讨论如下：

①当m=0时，式(1)显然恒成立；

②当m>0时，得m-2b≥0，即m≥2b，又-1≤b≤1，所以m≥2.

③当m<0时，得m-2b≤0，即m≤2b，又-1≤b≤1，所以m≤-2.

综上所述,实数m的取值范围是(-∞,2]∪{0}∪[2,+∞).

点评对于数学解答题(特别是立体几何中的计算问题)，往往是先判断后证明，然后才能应用这一解题程序. 就本题而言，先判断函数f(x)在[-1,1]上是增函数，从而有最大值f(1)=1, 最后将恒不等式进行等价转化，从而解决问题.

3 运算要简捷

运算简捷是运算的第三要求.

解由a≠0,b≠0,且

可知c,d都不是零向量.由c⊥d,得c·d=0，即

c·d=[a+(sinα-3)b]·[-ka+(sinα)b]=

-ka2+[sinα-k(sinα-3)](a·b)+

(sinα-3)sinα·b2=0,

得

又由

-1≤sinα≤1，

得

又k≠0，故实数k的取值范围是

点评本题若先计算向量c,d的坐标，然后再用向量数量积的坐标表示去计算，容易出错.因此，运算一定要简捷，这样可节省大量的书写时间，并能有更充足的时间去思考其他题目.

4 运算要巧妙

运算巧妙是运算的第四要求.

例4已知平面上的3个单位向量a,b,c，两两夹角均为120°.若|ka+b+c|>1，求实数k的取值范围.

解由向量加法的平行四边形法则，结合已知条件，得

a+b+c=0，

于是

ka+b+c=(k-1)a+a+b+c=(k-1)a.

又由|ka+b+c|>1，得

|(k-1)a|>1,

即

|k-1|>1，

解得

k>2或k<0.

故实数k的取值范围是(-∞,0)∪(2,+∞).

注意本题若按常规方法往往是将|ka+b+c|>1转化为(ka+b+c)2>1，然后再用数量积去解决，十分繁杂.

例5已知圆x2+y2+x-6y+m=0与直线x+2y-3=0相交于点P,Q，其中Q为原点，且OP⊥OQ，求实数m的值.

解OP⊥OQ等价于以PQ为直径的圆经过原点O.过圆x2+y2+x-6y+m=0与直线x+2y-3=0交点的曲线系方程为

x2+y2+x-6y+m+λ(x+2y-3)=0,

即x2+y2+(1+λ)x+(2λ-6)y+m-3λ=0.

要使此圆以PQ为直径，且过原点O(0,0)，则

解得

m=3.

点评在运算过程中，能巧解的要巧解，不要受“通性通法”的约束与限制，运算巧妙是运算的最高要求.

高考对考生运算能力的要求无处不在,而多数考生在高考中失分的最重要原因是运算能力不过关.因此，加强对运算能力的训练是备考中的重头戏，在复习中不仅要熟悉运算的一些常见方法，更要归纳总结运算技巧，譬如整体处理、估算或近似计算、数形结合、以算代证等.

精题集粹

( )

2.据2002年3月5日九届人大五次会议《政府报告》：2001年国内生产总值达到95 933亿元，比上年增长7.3%.如果“十五”期间(2001—2005年)每年的生产总值都按此年增长率增长，那么到“十五”末我国国内生产总值约为

( )

A.115 000亿元 B.120 000亿元

C.127 000亿元 D.135 000亿元

( )

(2007年天津市数学高考文科试题)

5.设等比数列{an}的公比为q，前n项和为Sn，若Sn+1，Sn，Sn+2成等差数列，则q的值为________.

(2005年湖北省数学高考试题)

6.设P1(x1,y1),P2(x2,y2)是圆x2+y2=1内相异的2个点，(x,y)是以P1P2为直径的圆上任意一点，求证：x2+y2<2.

7.设集合A={x|x2+(a+2)x+1=0,x∈R}，若A∩{x|x>0}=φ，求实数a的取值范围.

参考答案

1. C 2. C 3.D

6.证明由P1(x1,y1),P2(x2,y2)是圆x2+y2=1内相异的2个点，得

(2)

(3)

因为(x,y)是以P1P2为直径的圆上任意一点，所以(x,y)满足方程

整理得

x2+y2-(x1+x2)x-(y1+y2)y+x1x2+y1y2=0.

于是

x2+y2= (x1+x2)x+(y1+y2)y-x1x2-y1y2≤

x1x2-y1y2=

将式(2)，式(3)代入，得

x2+y2<2.

7.解设使A∩{x|x>0}≠φ的实数a的取值集合为M. 由于二次函数y=x2+(a+2)x+1的图像过点(0,1)，因此

解得

a≤-4.

故所求实数a的取值范围是CRM={a|a>-4}.