立体几何中的折叠、展开与动点问题

● (绍兴市第一中学 浙江绍兴 312000)

1 考查要求

立体几何中的折叠、展开与动点问题着眼于对学生空间思维能力的考查，立体几何中有许多形式各异的折叠问题.一个平面图形经折叠后成为一个空间图形,此时图形的结构发生了突变,从二维的平面图形一跃成为三维的空间图形.而以立体几何为载体的轨迹问题能将立体几何与解析几何巧妙地结合起来，常常涉及函数、数形结合、建模、化归等数学思想与方法,立意新颖，综合性强,能力要求高,教师在教学中可集中讲解这类问题.

2 考点回顾

近几年的高考试题比较注重考查知识的整体性和交汇性.立体几何中的轨迹问题将立体几何与解析几何有机地结合起来,解决此类问题的关键是把空间问题转化为平面问题，然后再根据曲线的定义或用解析法求出轨迹方程.立体几何中的折叠、展开问题则要特别注意空间图形与平面图形之间的相互联系.一般地，在同一半平面内的几何元素之间的关系是不变的，涉及到2个半平面内的几何元素之间的关系是要变化的，分别位于2个半平面内,但垂直于翻折棱的直线翻折后仍然垂直于翻折棱.在浙江省近3年的数学高考试题中，最近2年考查这方面的问题有所抬头，2008年考查1个选择题，2009年考查1个填空题，问题立意新、思维能力要求高，值得关注.

3 命题走势

立体几何中的折叠、展开问题需要学生有空间想象力，难度大且思维能力要求高.动点轨迹问题是较为新颖的一种创新命题形式，它重点体现了在解析几何与立体几何的知识交汇处设计图形，不仅能考查立体几何点、线、面之间的位置关系，而且能巧妙地考查求轨迹的基本方法.由于知识点多，数学思想和方法考查充分，因此笔者预计2010年高考会出这方面的试题.

4 典例剖析

4.1 折叠问题

例1一张正方形的纸ABCD，BD是对角线，过AB,CD的中点E,F的线段交BD于点O，以EF为棱，将正方形的纸折成直二面角，则∠BOD等于

( )

A.120° B.150° C.135° D.90°

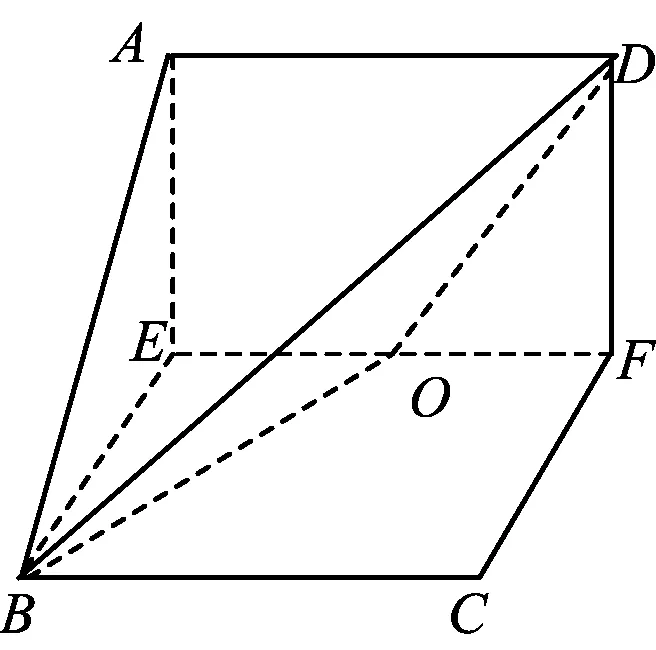
图1

又在△BOD中，由余弦定理可得

所以

∠BOD=120°.

评注本题为折叠问题中的空间角问题，此类问题要求学生清楚折叠前后的哪些量发生了变化，此外，还要注意找出空间转化为平面的途径和几何计算的准确性等.

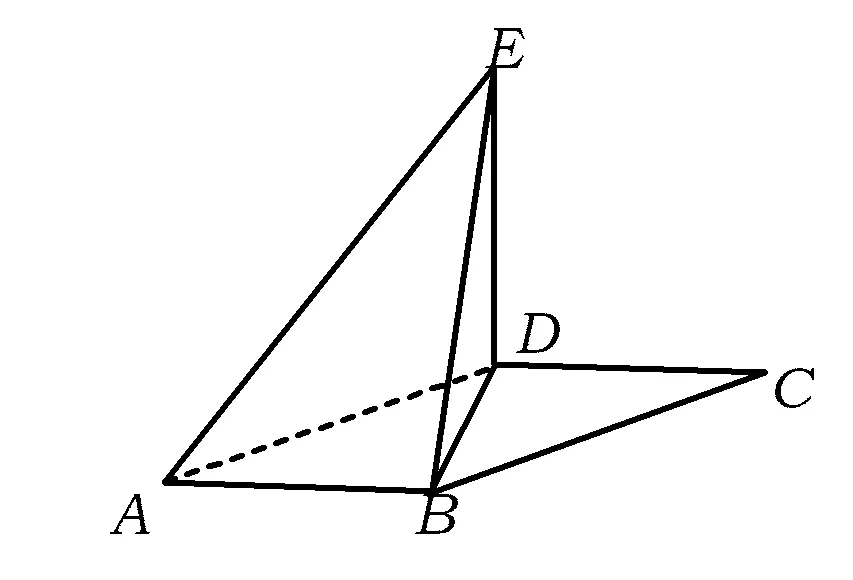
图2

例2如图2，在平行四边形ABCD中，∠DAB=60°，AB=2,AD=4,将△CBD沿BD折起到△EBD的位置，使平面EDB⊥平面ABD.

(1)求证：AB⊥DE;

(2)求三棱锥E-ABD的侧面积.

(2009年福建省数学高考文科试题)

分析(1)在△ABD中，由AB=2,AD=4,∠DAB=60°，得

于是

AB2+BD2=AD2,

得

AB⊥BD.

又平面EBD⊥平面ABD，平面EBD∩平面ABD=BD,AB⊂平面ABD，得AB⊥平面EBD.由DE⊂平面EBD,得AB⊥DE.

(2)由第(1)小题知

AB⊥BD,CD∥AB,

从而

CD⊥BD,

于是

DE⊥DB.

在Rt△DBE中，由

得

又由AB⊥平面EBD,BE⊂平面EBD，得AB⊥BE.因为

BE=BC=AD=4,

所以

由DE⊥BD,及平面EBD⊥平面ABD，得ED⊥平面ABD,而AD⊂平面ABD,从而ED⊥AD.因此

评注本题为折叠中的面(体)积问题，解决折叠问题的关键：

(1)画好2个图——翻折前的平面图和翻折后的立体图，常常画在一起；

(2)分析好2个关系——翻折前后哪些位置关系和度量关系发生了变化，哪些没有改变.

4.2 展开问题

(2006年江西省数学高考试题)

分析连结A1B，沿BC1将△CBC1展开与△A1BC1在同一个平面内，如图4所示.连结A1C，则A1C的长度就是所求的最小值.

通过计算可得∠A1C1C=90°.由∠BC1C=45°，得

∠A1C1C=135°,

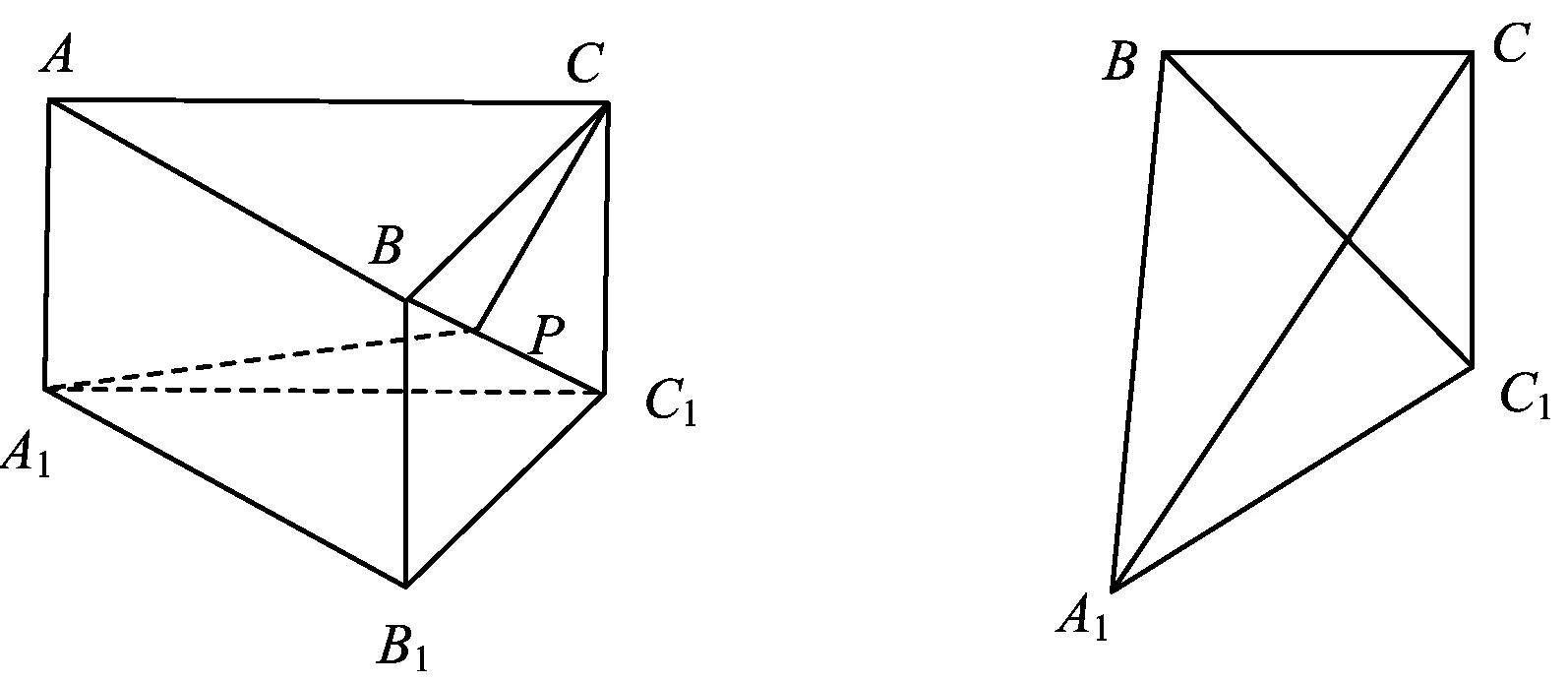
图3 图4

评注本题是展开问题中的两点距离问题，即求从一点出发沿几何体表面到另一点的最短距离问题，通常把几何体的侧面展开转化为平面图形中的两点距离问题.

(1)请在图中设计一种虚线，沿虚线翻折可成原来的三棱锥(指三棱锥的3个面);

(2)求这个三棱锥外接球的体积.

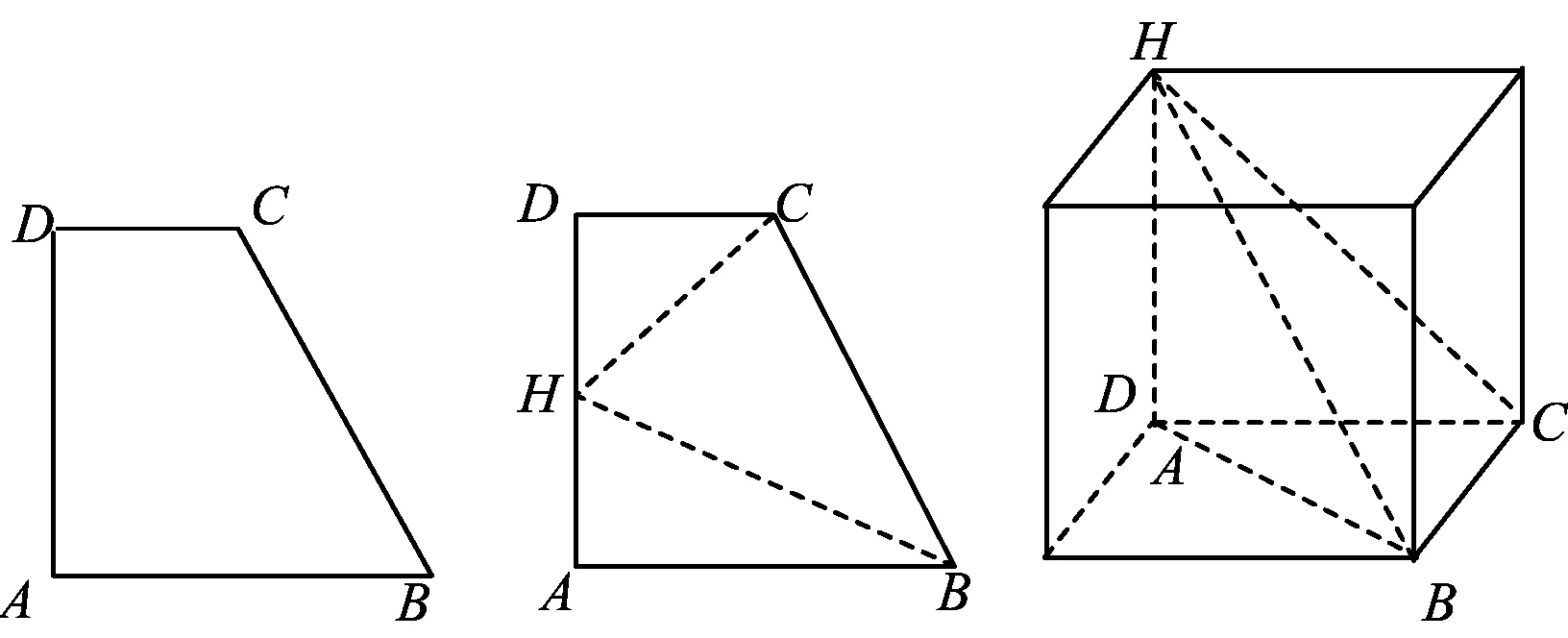
图5 图6 图7

分析(1)如图6,取AD的中点H，连结HC，HB，则HC，HB为设计的虚线.

(2)如图7,将三棱锥补成长方体.可视长方体的对角线为HB，其长度就是外接球的直径

因此

故

评注本题是展开问题中的体积问题，要解决此剪拼问题,必须弄清4个面都是直角三角形的三棱锥形状，仔细观察发现其中有3个直角三角形必须有1条直角边长相等.对第(2)小题还可以利用取BH的中点O，证明OB=OH=OA=OC的方法来求外接圆的体积.

4.3 轨迹问题

例5平面α的斜线AB交α于点B，过定点A的动直线l与AB垂直，且交α于点C，则动点C的轨迹是

( )

A．1条直线 B．1个圆

C.1个椭圆 D.双曲线的1支

(2006年北京市数学高考试题)

分析设l与l′是其中的2条任意的直线，则这2条直线确定一个平面，且斜线AB垂直于这个平面.由过平面外一点有且只有一个平面与已知直线垂直可知,过定点A与AB垂直的所有直线都在这个平面内，故动点C都在这个平面与平面α的交线上.故选A．

评注本题利用定义法，借用2个平面相交有1条交线的定义，以空间直线与平面的位置关系为依据，研究平面解析几何的点的轨迹问题，立意新颖、构思巧妙，是深入考查学生思维能力的上乘之作.

例6P为四面体S-ABC的侧面SBC内一点，若动点P到底面ABC的距离与点P到点S的距离相等，则动点P的轨迹是侧面SBC内的

( )

A．椭圆的一部分

B．椭圆或双曲线的一部分

C．双曲线或抛物线的一部分

D．抛物线或椭圆的一部分

分析(1)当面SBC⊥面ABC时，过点P作PH⊥BC于点H，则PH⊥面ABC，于是|PH|=|PS|.由抛物线定义知，点P的轨迹为抛物线在面SBC内的一部分.

(2)当面SBC不垂直于面ABC时，过点P作PG⊥面ABC于点G，过点G作GH⊥BC，则BC⊥PH.因此在Rt△PGH中，

又

所以由椭圆定义知点P的轨迹为椭圆在面SBC内的一部分.

故选D．

评注对于立体几何中的轨迹问题，我们往往会想到用圆锥曲线的第二定义去解决，关键是要找到有关的定点与相应的定直线.本例通过回归定义法，将空间问题平面化，通过动中找定，寻找定点与定直线,从而达到解题的目的.

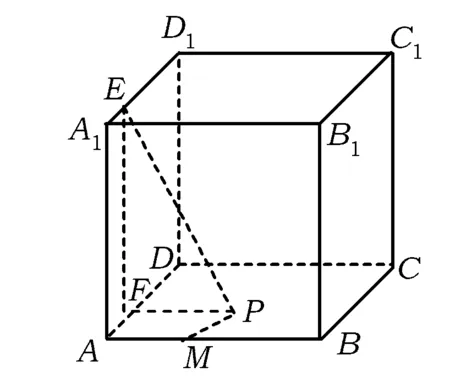
图8

( )

A．抛物线B．双曲线

C．直线 D．圆

分析过点P作PF⊥AD于点F，连结EF，则PE是点P到直线A1D1的距离.由题意得

PE2-PM2=1.

因为

PE2=PF2+1，

所以

PM=PF.

在平面ABCD内，由抛物线定义知所求点P的轨迹是抛物线.故选A.

评注本例是用解析法求出轨迹方程，把立体几何中的轨迹问题转化成解析几何中曲线的定义加以求解，其实质就是解析几何中曲线定义的平面的立体化，还得紧紧抓住解析几何中曲线的定义，通过解析几何中曲线的定义达到解答立体几何中轨迹问题的目的.

精题集粹

1．如图9，在正三角形ABC中，D，E，F分别为各边的中点，G，H，I，J分别为AF，AD，BE，DE的中点.将△ABC沿DE，EF，DF折成三棱锥以后，GH与IJ所成角的度数为

( )

A．90° B．60° C．45° D．0°

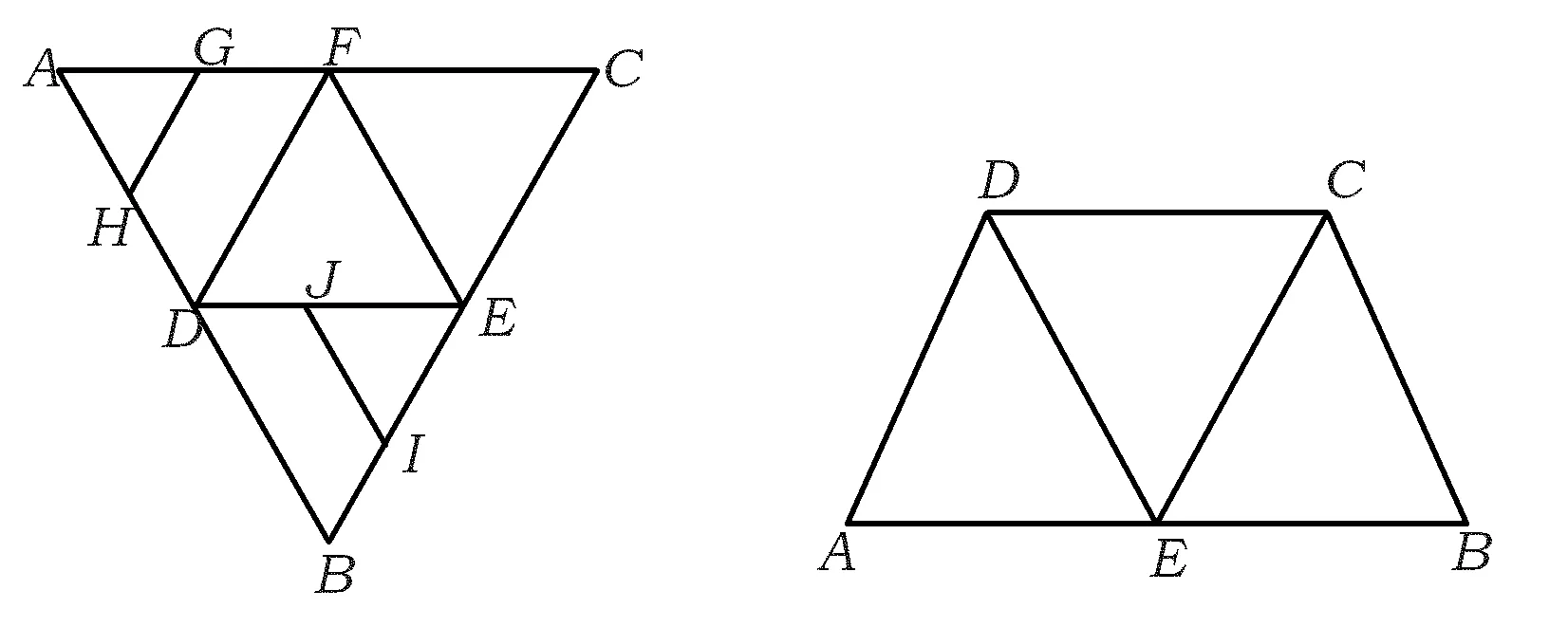
图9 图10

2．如图10，在等腰梯形ABCD中，AB=2DC=2,∠DAB=60°,E为AB的中点，将△ADE与△BEC分别沿ED，EC向上折起，使点A，B重合于点P，则P-DCE三棱锥的外接球的体积为

( )

( )

A．4个点 B．2条直线

C．双曲线的1支 D．1个圆

4．已知在菱形ABCD中，AB=2，∠A=120°，沿对角线BD将△ABD折起，使二面角A-BD-C为120°，则点A到△BCD所在平面的距离等于________．

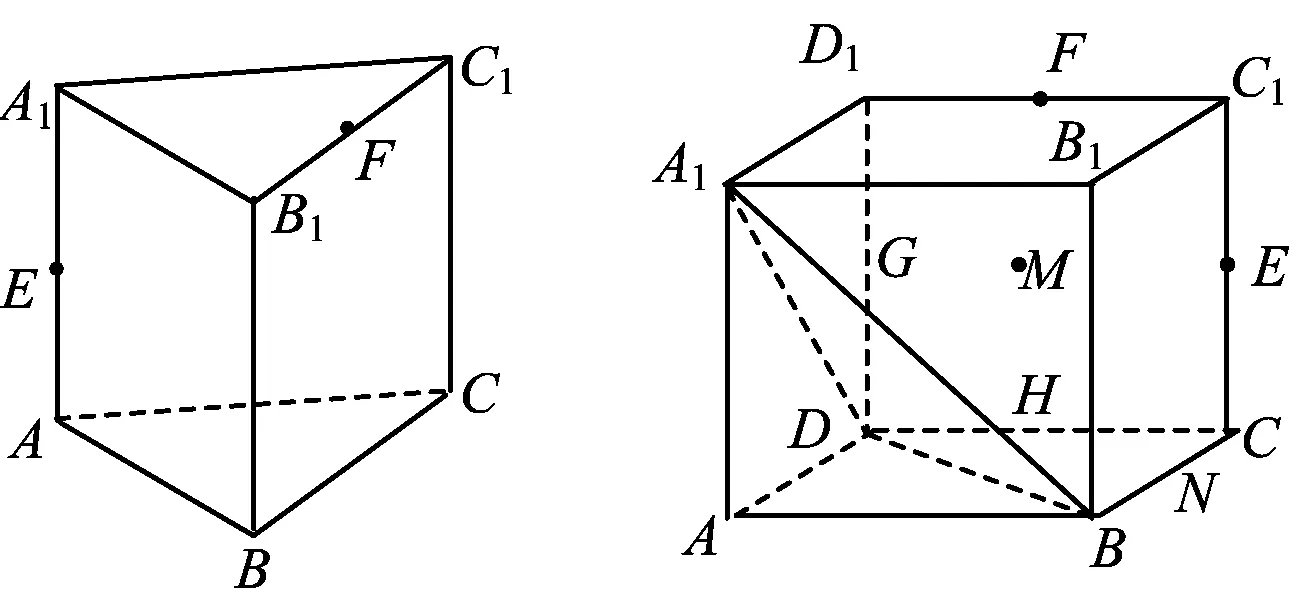
图11 图12

6．如图12,在正方形ABCD-A1B1C1D1中,边长为a,E,F,G,H分别是CC1,C1D1,D1D,CD的中点，N是BC的中点，M在四边形EFGH上及其内部运动.若MN∥平面A1BD，则点M轨迹的长度是________.

参考答案

1.B 2.C 3.A

图13

从而

(1-λ,-λ,λ-1),

(-λ,1-λ,λ-1).

显然∠APC不是平角，因此∠APC为钝角等价于

(1-λ)(-λ)+ (-λ)(1-λ)+(λ-1)2=

(λ-1)(3λ-1)<0，

解得