承力筒模态分析与测试
2010-06-08张红英
姚 骏,张红英,崔 伟,杜 胜
(上海卫星工程研究所,上海 200240)
1 前言
承力筒承载卫星主要载荷,是卫星结构组装的核心,是影响卫星结构强度、连接刚度和整星动态频率特性等性能的关键主承力结构[1]。承力筒设计与制造的质量成为卫星研制过程中关注的焦点。
模态试验可以确定结构的传递特性(包括模态频率、模态振型、模态阻尼比等模态参数);检查结构动态特性是否符合设计要求,发现其结构设计缺陷,为结构修改提供依据;为结构数学模型的验证和修改、响应预示、振动控制、稳定性分析以及航天器与运载火箭的动力学耦合分析等提供依据[2-4]。因此,对承力筒进行模态试验是了解其结构特性的重要手段。
本文分别用悬挂和固支两种测试方法对某卫星的两种结构设计的承力筒进行了模态测试与分析,并阐述了这两种测试方法对测试结果的影响。
2 承力筒的结构设计
某卫星承力筒是采用整体形式,由筒体、端框、贮箱安装框和纵向连接件(桁条)等组成。其中,筒体推进舱段为锥形,服务舱段为柱形,下端外径为φ910 mm,上端外径为φ500 mm,整筒高度为1 238 mm。承力筒筒体是由碳纤维T300-3K面板和铝蜂窝组成的夹层结构。承力筒除下端框采用铝合金锻材LD10CS之外,其他端框(上端框、中端框、贮箱上安装框、贮箱下安装框)、端框加强件和纵向连接件均采用 T700S-12K碳纤维模压成型。承力筒设计质量为22.5 kg。
根据型号的研制需要,先后对承力筒进行了两轮设计。承力筒Ⅱ是在承力筒Ⅰ上进行的改进和优化,两种设计的外形尺寸保持一致。两种承力筒结构见图1,它们技术状态的差异性比较见表1。
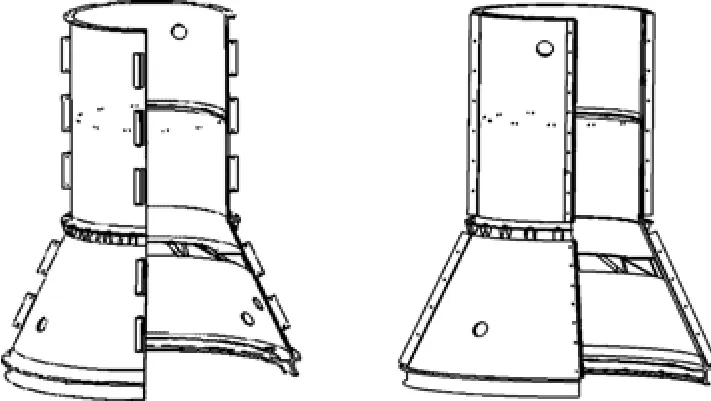
图1 承力筒结构示意图(左为承力筒Ⅰ,右为承力筒Ⅱ)Fig.1 Structure schematic diagram of the loaded cylinder(before and after optimization)
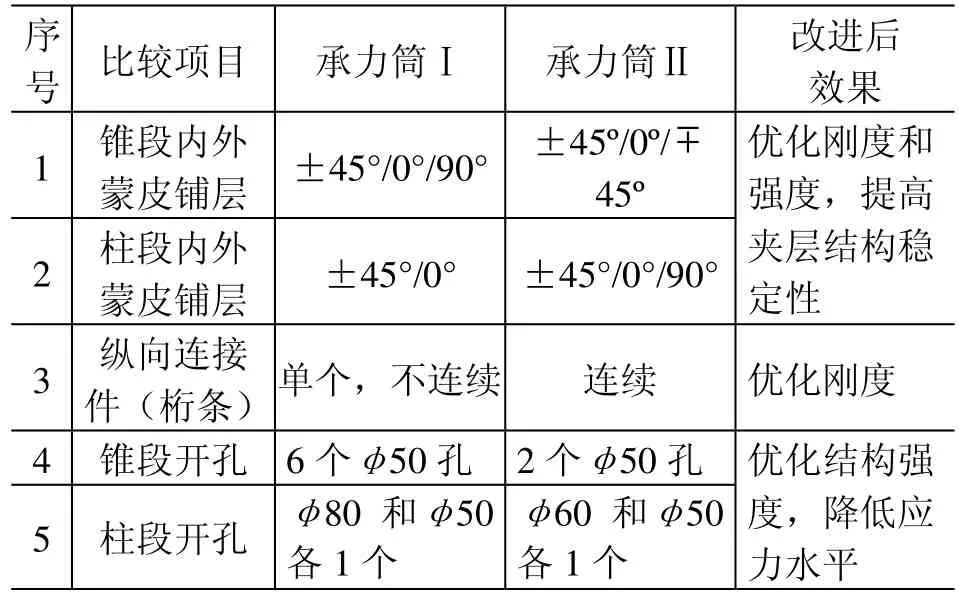
表1 承力筒两种状态的结构设计差异性比较表Table 1 The structure differences of the loaded cylinder before and after optimization
3 承力筒的模态分析与试验
3.1 模态分析(固支法)
根据设计参数,利用MSC/Patran软件建立了承力筒Ⅰ、承力筒Ⅱ的有限元模型,端框及桁条离散成梁单元,筒体按层合板离散成板壳单元。利用MSC/Nastran软件分别对两个模型进行了固定于地基的模态计算。承力筒Ⅰ、Ⅱ的有限元模型见图2,其振型参见图 3、图 4,分析结果见表 2。从理论分析可以看出承力筒Ⅱ的基频大于承力筒Ⅰ。
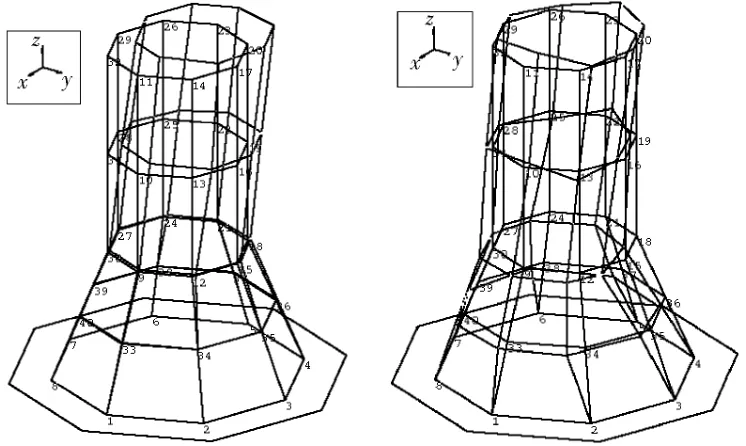
图2 采用固支法的承力筒有限元模型(左为承力筒Ⅰ,右为承力筒Ⅱ)Fig.2 The FEM model of the cylinder by fixing method (before and after optimization)
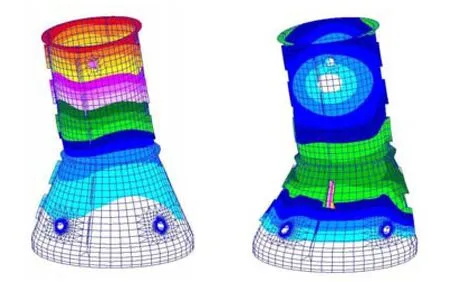
图3 承力筒Ⅰ采用固支法的模态分析振型图(左为一阶,右为二阶)Fig.3 The calculated modal shapes of the loaded cylinder Ⅰ(before optimization) by fixing method (the left is mode 1, the right is mode 2)
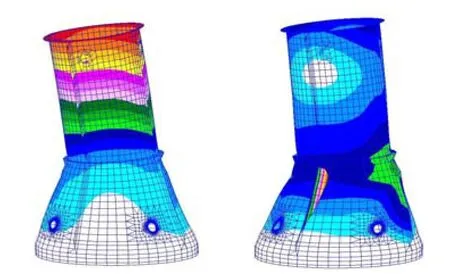
图4 承力筒Ⅱ采用固支法的模态分析振型图(左为一阶,右为二阶)Fig.4 The calculated modal shapes of the loaded cylinder Ⅱ(after optimization) by fixing method (the left is mode 1,the right is mode 2)

表2 采用固支法的模态分析结果Table 2 The modal analysis results of the cylinder by fixing method
3.2 模态试验
为了验证承力筒产品整体模态特性与分析导出值的一致性,为修正整星分析模型和鉴别承力筒频率特性对整星总体模态特性的影响分析、进一步对承力筒优化设计提供依据,进行了单筒状态下的模态试验。
对于产品的模态试验,一般采用固支法或悬挂法。采用固支法时,要求支承基础的固有频率一般应高于结构分析最高阶固有频率的5倍,支撑基础的质量一般应大于卫星质量的10倍。采用悬挂法时,要求悬挂系统的固有频率应小于试件一阶固有频率的1/5。
3.2.1 承力筒Ⅰ的模态试验(悬挂法)
在上海交通大学进行了承力筒Ⅰ的模态试验。由于上海交通大学试验室的地基频率约为300 Hz,而承力筒的基频在 200~300 Hz之间,因此当时不能采用固定于地基的方法,只能采用悬挂法,所以选取的试验方法是带底座的近似悬挂法。底座采用钢材制成,质量为163 kg。试验状态参见图5,测试结果见表3,振型见图6。

图5 承力筒Ⅰ采用悬挂法的模态试验现场图Fig.5 The modal test scene of the loaded cylinder I by hanging method
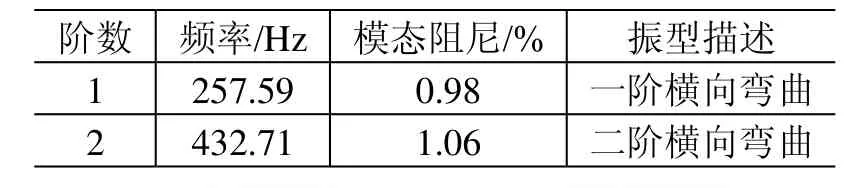
表3 承力筒Ⅰ采用悬挂法的模态试验结果Table 3 The modal test results of the loaded cylinder I by hanging method
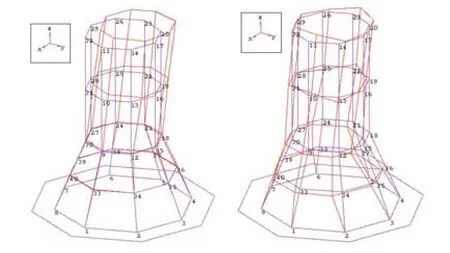
图6 承力筒Ⅰ采用悬挂法的模态试验振型图(左为一阶,右为二阶)Fig.6 The test modal shapes of the loaded cylinder I by hanging method (the left is mode 1, the right is mode 2)
3.2.2 承力筒Ⅱ的模态试验(固支法)
承力筒Ⅱ在上海卫星工程研究所进行了模态试验。该试验地基基频为980 Hz,远大于承力筒一阶固有频率,因此将承力筒固定于地基上进行模态试验,即承力筒通过三段120°的压环压在下端框与地基固连;激振方法为锤击法,锤击位置位于承力筒上端面。试验状态参见图7,测试结果见表4,振型见图8。

图7 承力筒Ⅱ采用固支法的模态试验现场图Fig.7 The modal test scene of the loaded cylinder II byfixing method
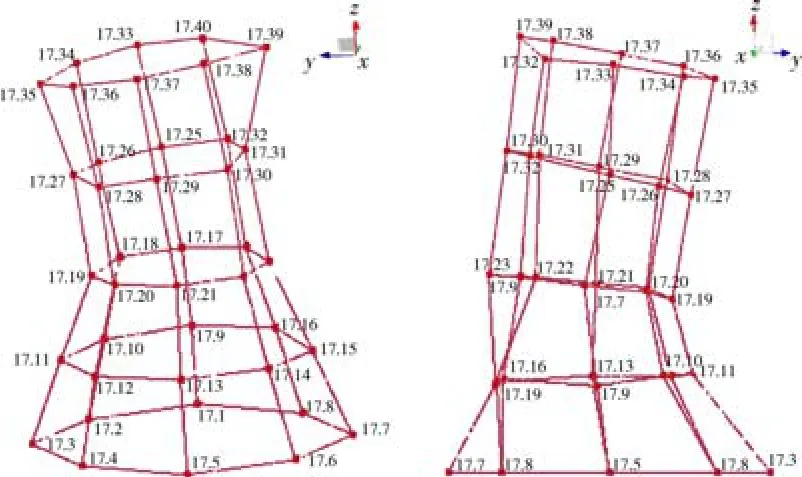
图8 承力筒Ⅱ采用固支法的模态试验振型图(左为一阶,右为二阶)Fig.8 The test modal shapes of the loaded cylinder Ⅱ by fixing method
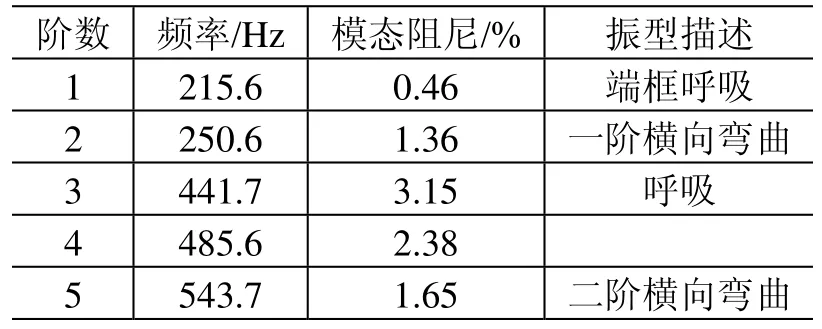
表4 承力筒Ⅱ采用固支法的模态试验结果Table 4 The modal test results of the loaded cylinder II by fixing method
从表3、表4可以看出,对于整星频率影响最大的一阶弯曲,优化后的承力筒Ⅱ的频率没有提高,反而有一定程度的下降,这与最初的设计分析不相符。经分析,承力筒两种试验状态的差别是造成该问题的主要原因。
3.3 补充模态分析(悬挂法)
根据承力筒Ⅰ带底座的近似悬挂法试验时的技术状态,对承力筒Ⅰ、Ⅱ分别建立了带悬挂工装的有限元模型,随后进行了模态计算。承力筒Ⅱ的有限元模型见图9,两个承力筒的模态分析振型分别见图10、图11,分析结果见表5。分析结果表明,承力筒在不同的状态下模态特性存在一定的差异性。比较表2、表5的结果可以看出,通过悬挂法得到的承力筒模态频率较通过固支法得到的模态频率偏高。
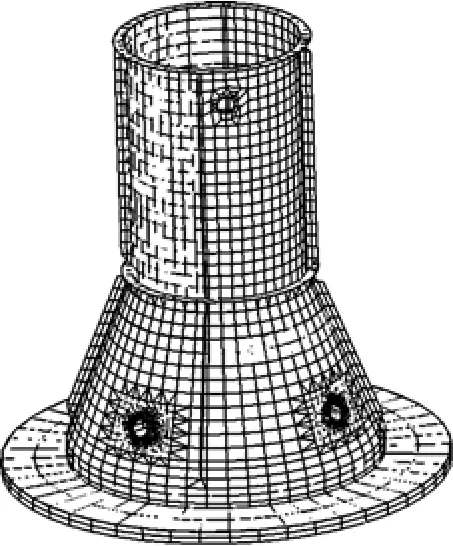
图9 承力筒Ⅱ采用悬挂法的有限元模型图Fig.9 The FEM model of the loaded cylinder II by hanging method
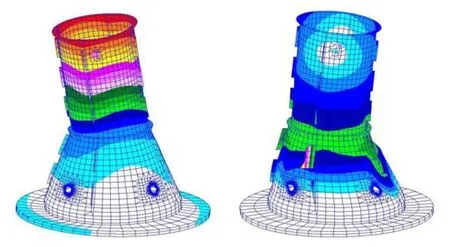
图10 承力筒Ⅰ采用悬挂法的模态分析振型图(左为一阶,右为二阶)Fig.10 The calculated modal shapes of the loaded cylinder Ⅰ by hanging method (the left is mode 1,the right is mode 2)
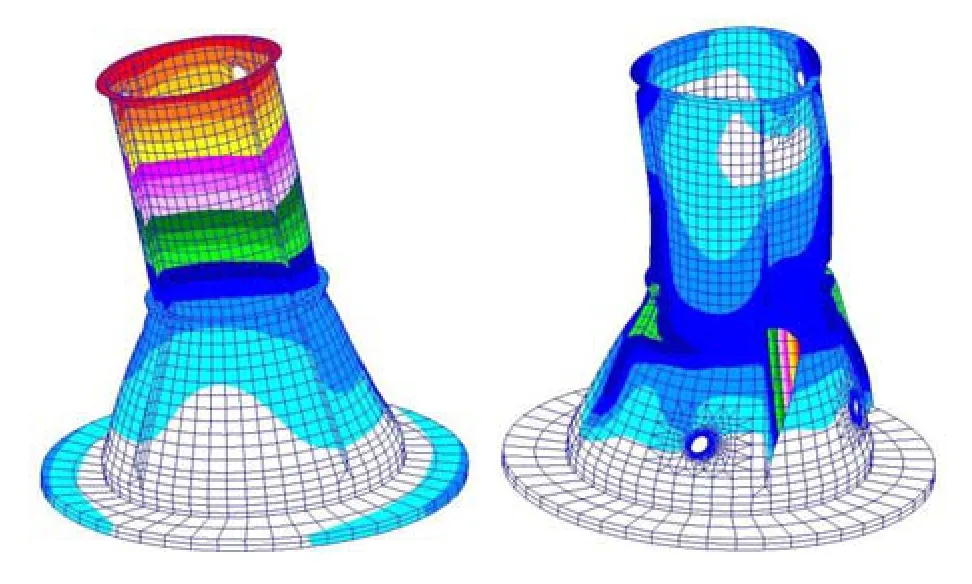
图11 承力筒Ⅱ采用悬挂法的模态分析振型图(左为一阶,右为二阶)Fig.11 The calculated modal shapes of the loaded cylinderⅡby hang method (the left is mode 1, the right is mode 2)
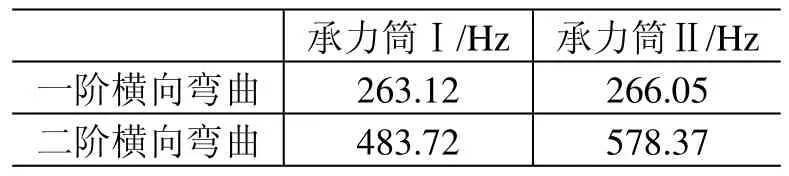
表5 承力筒采用悬挂法的模态分析结果Table 5 The modal analysis results of the loaded cylinder by hanging method
3.4 补充模态试验(悬挂法)
为了进一步验证分析结果、更加深入细致地比较承力筒Ⅰ、Ⅱ的差别,在上海卫星工程研究所利用与承力筒Ⅰ模态试验状态一致的底座、采用悬挂法进行了承力筒Ⅱ的模态试验。试验状态见图12,测试结果见表6,振型见图13。

图12 承力筒Ⅱ采用悬挂法的模态试验现场图Fig.12 The modal test scene of the loaded cylinder II by hang method
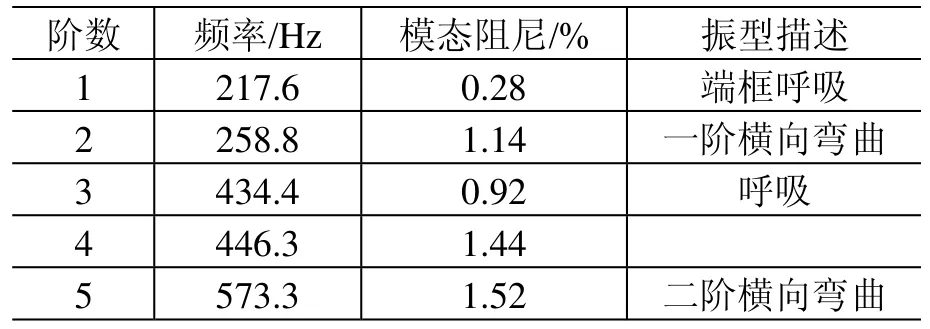
表 1 承力筒Ⅱ采用悬挂法的模态试验结果Table 6 The modal test results of the loaded cylinder II by hanging method

图13 承力筒Ⅱ采用悬挂法的模态试验振型图(左为一阶,右为二阶)Fig.13 The test modal shapes of the loaded cylinder Ⅱby hanging method (the left is mode 1, the right is mode 2)
3.5 模态分析与试验结果的比较
有关承力筒模态频率的分析与试验的主要数据见表7。由于悬挂法引入了附加系统,而附加系统的质量与刚度均远大于承力筒的质量与刚度,此时在悬挂法下的系统模态体现为承力筒的局部模态,因此与承力筒在固支法下的模态具有一定的可比性。承力筒在固支法和悬挂法两种不同的边界条件下得出的一阶、二阶横向弯曲的振型近似,分析与试验结果吻合。但毕竟导入了附加系统,悬挂法下承力筒的模态特性因其影响而有所差异,所以承力筒的模态特性应为通过固支法下得到的模态特性。
从表 7可以看出,承力筒Ⅱ相比承力筒Ⅰ在刚度特性上有一定的加强,这与设计的初衷是一致的。
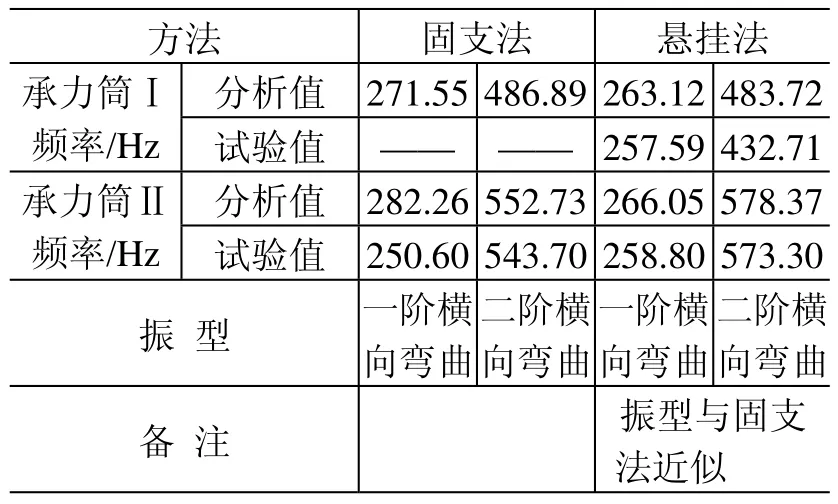
表7 承力筒模态频率的分析、试验数据汇总表Table 7 Comparison between analysis and test results for the loaded cylinder
4 结束语
模态试验的目的是确认模态分析的有效性,提供试验数据来修正有限元模型并重新进行分析。
对承力筒进行模态试验是确认卫星结构研制质量的关键环节,选择合理的试验手段和方法显得尤为重要,值得研制人员关注。
(References)
[1]袁家军.卫星结构设计与分析[M].北京: 中国宇航出版社, 2004-04
[2]GJB 2497—1995, 卫星结构试验方法[S]
[3]GJB 2706A—2008, 航天器模态试验方法[S]
[4]李宁, 冯咬齐, 岳志勇.卫星承力筒结构的模态试验方法探讨[J].航天器环境工程, 2009, 26(4): 365
