三维动态混合网格在AUV发射过程中的应用

吴利红，封锡盛，胡志强

（1中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳 110016；2中国科学院研究生院，北京 100049）

三维动态混合网格在AUV发射过程中的应用

吴利红1,2，封锡盛1，胡志强1,2

（1中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳 110016；2中国科学院研究生院，北京 100049）

为研究AUV从有界流场自航发射到无界流场的运动边界的扰流场，文章采用了三维动态混合网格方法进行数值模拟的策略。混合网格由三菱柱/四面体/六面体网格构成，当AUV运动时，靠近AUV的三菱柱网格随AUV运动，外层是静止的六面体网格,中部的四面体网格随AUV运动而变形或者重构。数值仿真结果给出了不同时刻AUV表面的压力分布、整个航程AUV的阻力系数变化，其值与理论结果吻合。同时研究了直径比对发射管航行的附加质量和阻力系数的影响，这为水下对接AUV提供了有效手段。

AUV；自航发射；三维混合网格；非结构动网格；水下对接

1 引 言

求解包含运动边界的非定常扰流场问题，如自由表面、多体相对运动和流体与结构耦合等问题，是计算流体力学中的一个难点。动态混合网格方法是近年来出现的解决运动边界的有效方法，即采用混合网格对复杂区域进行网格划分，采用非结构动网格实现运动边界的网格处理。

应用混合网格对定常扰流下复杂区域的网格划分较为成熟，已发展了多种混合网格：三菱柱/四面体、四面体/三菱柱/金字塔，四面体/自适应直角坐标网格、直角坐标网格/四面体/三菱柱[1]。应用非结构动网格对二维或者小振幅的运动边界仿真的文献也日益涌现，主要用于解决空气动力学中机翼的振荡摆动[2]、二维机翼—外挂物分离[3]和控制翼偏转[4]等问题。将并行计算应用到定常流动问题也日益广泛，代表性的有夏健[5]对DLR_F6带攻角定常飞行流场采用1～8个分布式内存计算节点进行计算；Cavallo[6]采用并行网格自适应策略仿真多体分离的相对运动扰流场。

而将混合网格用于非定常运动中的网格划分、将非结构动网格应用到三维大位移运动和将并行计算用于运动边界的非定常计算中的研究较少。

本文采用动态混合网格结合并行计算实现了AUV从有界流场航行到无界流场的三维大位移扰流场的数值模拟，这为当前三维大位移的运动边界移动较难采用数值仿真实现的问题提供了方法上的借鉴，同时弥补了有关AUV从有界流场中自航发射的扰流场只有理论研究而缺少数值研究的不足[7-8]。

2 动态混合网格方法

2.1 混合网格生成

假设有界流场为一端封闭的管道，简称发射管，AUV自航发射在初始时刻的几何模型如图1所示。AUV和发射管直径比为0.625，AUV直径333mm，长3.8m；管长为8m。初始时刻，AUV尾部离发射管端部A点0.4m，首部离发射管口B点3.8m。数值仿真AUV自航发射的三维大位移绕流场包括AUV从初始位置开始，以3Kn速度从发射管中航行到发射管外的无界流场中的绕流，AUV总航程约15m。载体坐标系Oxyz建立在AUV重心G处，O点与G点重合。

整个流场的网格采用混合网格构成，包含三菱柱、四面体、六面体三种网格。网格拓扑结构如图2所示，包含4个网格区域，其中区域1为绕AUV表面的三菱柱区域；区域2为四面体网格；区域3是靠近发射管壁面的六面体网格区域；区域4为填充无界流场的四面体网格。

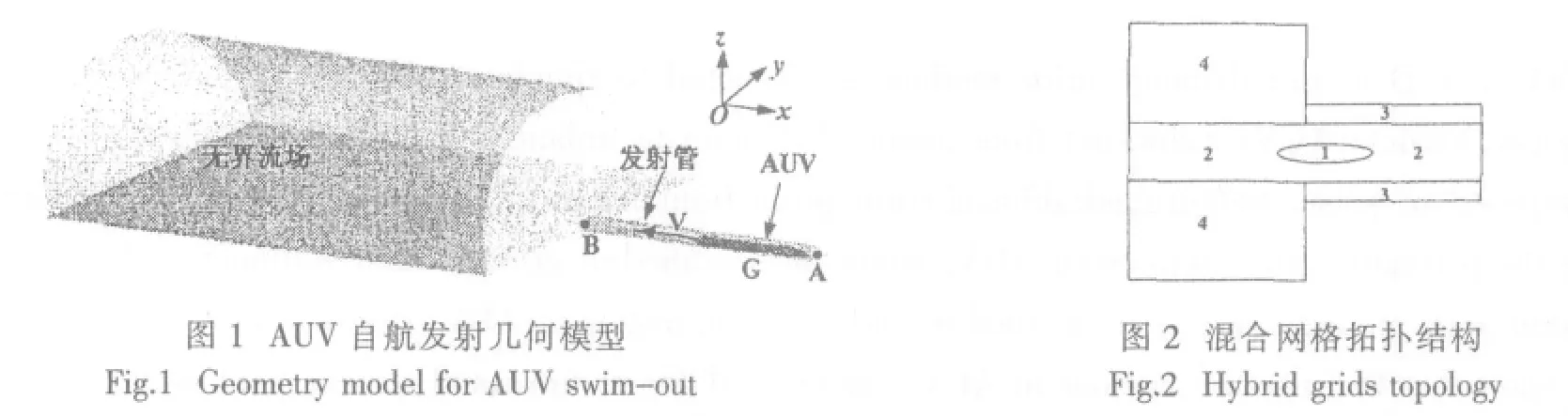
当AUV运动时，区域1随AUV运动；区域2变形；区域3和区域4静止不动。图3给出了初始时刻对称面上靠近AUV首部、AUV和发射管间隙处和靠近AUV尾部的网格分布，分别对应着图3中（a）、（b）、（c）图。

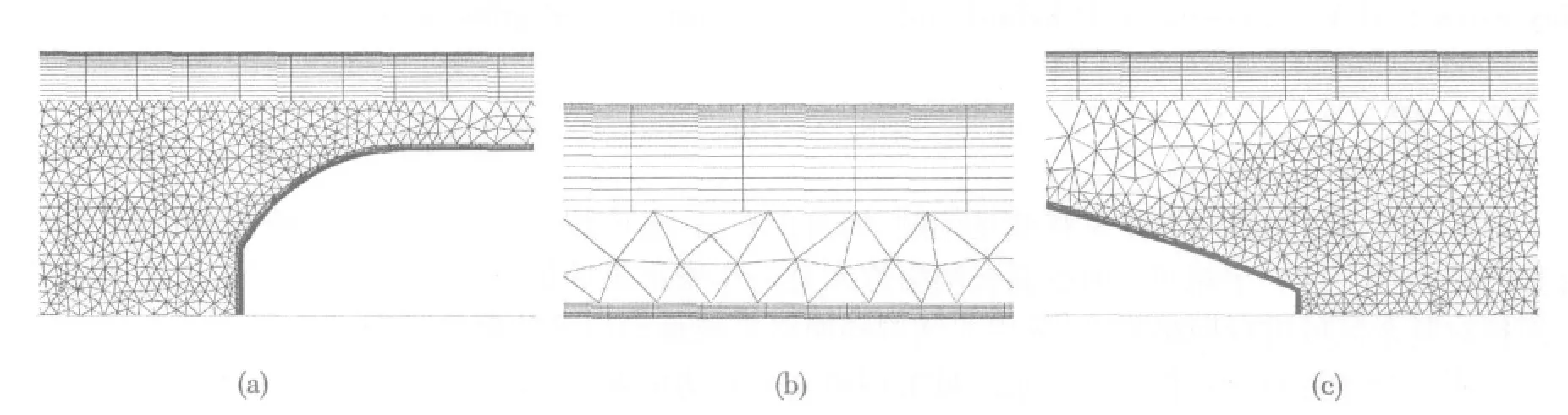
图3 初始时刻对称面上的网格分布Fig.3 Mesh in symmetry at initial time

2.2 动网格更新方法

动网格更新有三种方法：弹簧近似网格光顺法、动态层方法和局部网格重构方法。弹簧近似网格光顺法适用于小位移问题；动态层方法适应于单向运动；而局部网格重构方法适用于局部网格重构。第一种方法不改变网格的拓扑结构，这样能保证网格质量；后两种方法改变了网格的拓扑结构，新网格的变量需要从旧网格中插值得到。对于大位移和强切变问题仅靠节点松弛不能保证网格质量，而且有可能出现网格相交的情况。为了克服这一困难，本文采用弹簧近似网格光顺法和局部网格重构法相结合，解决大位移和强切变非定常流动的网格移动问题。

弹簧近似模型将四面体非结构网格看作是一个弹簧网格系统，每条边都认为是一根具有一定倔强系数的弹簧，初始状态下，每个节点都处于平衡状态，当边界运动时，节点i所受到的合力如公式（1）所示，节点i的网格更新后的位置如公式（2）所示，其中，分别表示节点i和临近节点j的位移，ni是节点i的临近节点数目，kij是连接节点i和邻近节点j的弹簧刚度系数。公式（2）中的， 分别表示n，n+1迭代时间步下的节点i的位置； 表示临近节点j在内循环m步后收敛后的位移，其中上标m，c分别表示内循环迭代步数，内循环收敛的状态。

当网格移动后，网格的品质会发生改变，表征网格的品质的参数如光顺性、正交性、节点分布特性，高宽比（aspect ratio）和单元尺寸会发生改变。局部网格更新通过设置网格控制参数如网格的最小、最大长度，网格单元的偏斜度、尺度函数参数可以控制网格移动后的品质，当网格不满足以上控制参数设置的值域时，网格被标示出，并在局部挖出一个小洞，取出洞的边界信息，然后利用阵面推进法重新生成网格并进行优化。为了使得重新生成的局部网格与全局网格保持一定的光顺性，对局部网格采用尺度函数进行控制。

3 并行计算

并行计算就是利用多个计算节点同时进行计算。合理的网格分区方法是有效并行计算的前提。网格分区时，需要选择生成网格的分割方法、设置分割数、选择区域和记录、以及使用的优化方法。其目标是生成等数量单元的网格分块、分割的接触面数最小、分割的领域数最小。本文通过对不同网格分区方法进行试验对比，确定出采用和初始网格拓扑结构一致的Cylindrical R axes的网格分区方法是合适的。

并行机的性能一般用加速比来评测。计算加速比的一般方法是：假设在一个处理器上运行某程序需时间T1，在P个节点（各节点的CPU性能一样）上运行此程序需时间Tp，则加速比Sr=T1/Tp，并行效率η=Sr/P。

本文将网格节点数分别为449,442和592,669的计算网格在1～12个计算节点上并行计算，获得其加速比如图4。从图4可以看出，加速比曲线与定常计算的正比曲线不一样[5]，采用8个计算节点具有最高加速比。

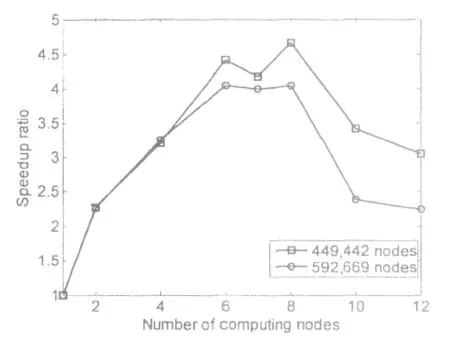
图4 并行计算加速比Fig.4 Speedup ratio for parallel computing

4 数值仿真

4.1 给定直径比的数值仿真结果

利用上述动态混合网格和动态并行计算方法，数值模拟了AUV从发射管中航行到无界流场的三维大位移运动边界的绕流，图5为t=2s时刻对称面上靠近首尾部的移动网格分布。

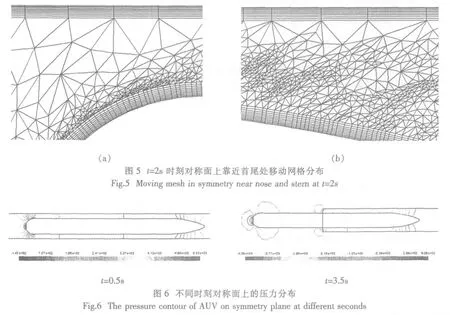
图6给出了不同时刻对称面上的压力分布，即t=0.5s时AUV在发射管内和t=3.5s时AUV通过发射管口的压力分布。图7是AUV从发射管航行到无界流场中全程约15m的阻力系数图，包括全程压差阻力系数Cp、摩擦阻力系数Cf和总阻力系数Ct，阻力系数与力的换算关系见公式（3），其中，F包含摩擦阻力、压差阻力和总阻力，C表示这三种系数，ρ为海水密度，V为AUV航速，A为AUV横截面面积。分析总阻力系数Ct，发现其在发射管内的阻力系数与Richard[7]采用控制体方法计算相应载体在无限长发射管中航行的阻力系数值2.58接近，Ct在无界流场中的阻力系数段与采用CFX软件计算定常来流获得的系数进行对比，其中摩擦阻力与CFX软件计算的定常值0.35接近。

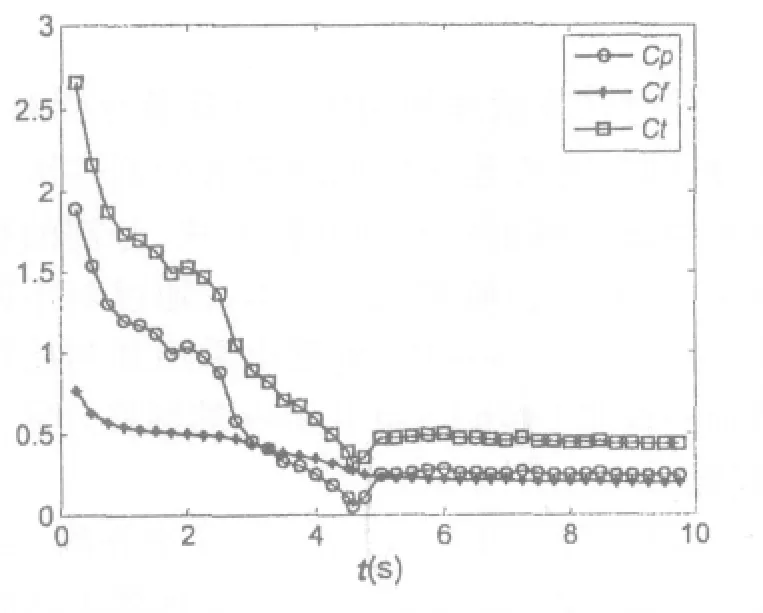
图7 AUV自航发射全程Cp，Cf和Ct Fig.7 Cp,Cf and Ct for AUV swim-out

从整个航程中还可以看出摩擦阻力系数的变化较小，而压差阻力变化较大，尤其是在发射管内，压差阻力占总阻力的71%，这主要是因为发射管内的有界边界的影响，导致两者的间隙流流速大大增加，压力大大下降。因此非常有必要研究在发射管中运动直径比对AUV航行阻力的影响。

4.2 改变直径比对AUV附加质量和航行阻力的影响

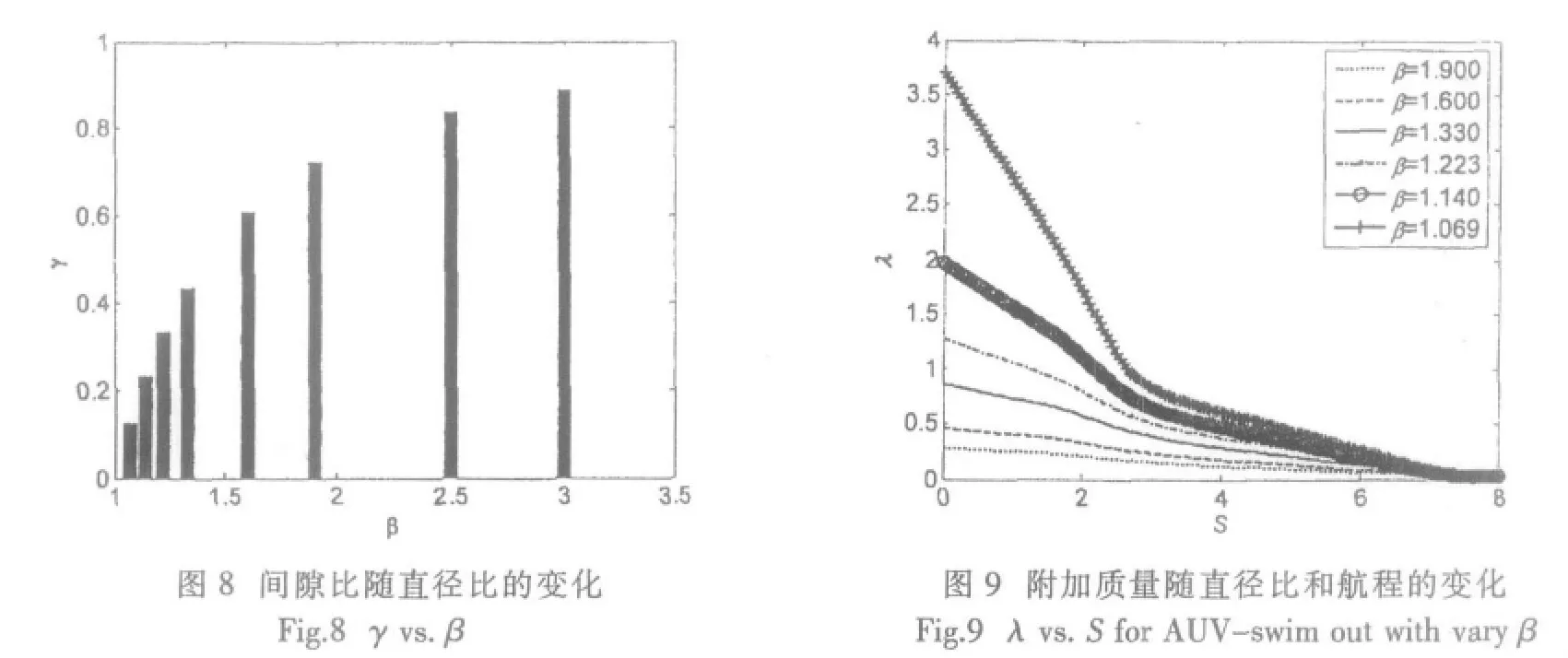
发射管中运动的直径比为β，如公式（4）所示，其中D为发射管直径，d为AUV直径。随着直径比的降低，间隙比γ（如公式（5）所示）越小，图8给出直径比与间隙比的关系。当AUV在不同直径发射管中航行时，其附加质量也会变化，附加质量mh与直径比的关系如公式（6）所示[7]，附加质量系数λ为附加质量与AUV所排开水的质量的比值，它与直径比的关系如公式（7）所示，附加质量随AUV航程S的关系见公式（8）所示。其中Λ为AUV排水体积；L为发射管长度，l为AUV长度,而且L＞l，l0为初始时刻AUV距离发射管底端长度。λ0为AUV完全在发射管内的附加质量系数。图9给出附加质量系数随航程和直径比的关系曲线，可以看出，随着直径比的减少，附加质量迅速增加；随着航程的增加，AUV渐渐靠近发射管口，其附加质量也减少。

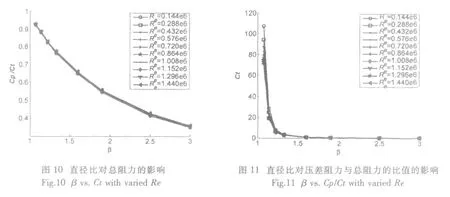
直径比不仅对附加质量有影响，对管道中航行的阻力也有较大的影响，其关系如图10所示，直径比减少，阻力迅速增加，当直径比小于1.223时，阻力曲线陡升，影响阻力的主要原因是间隙比减小，压差阻力大大增加，当直径比为1.07，间隙比为0.125时，压差阻力占总阻力的92.7%，如图11所示。从图10和图11可以看出相同直径比前提下，AUV以不同雷诺数Re航行，阻力系数变化较小。

5 结 论

本文采用三菱柱/四面体/六面体构成的动态混合网格数值仿真了AUV从发射管中自航发射的三维大位移运动过程，得到了如下结论：

（1）AUV从发射管航行到无界流场时，在发射管中的最大阻力约为无界流场中的7.4倍，阻力随着航程的增加而降低，当AUV尾部通过发射管发射管口时，阻力值降低到最小；

（2）发射管中运动时，当直径比小于2时，压差阻力占总阻力的主要成份，直径比为1.07，压差阻力约为总阻力的92.7%；

（3）发射管中运动时，附加质量和阻力系数都随直径比减小而迅速增大，而相同直径比下改变雷诺数对阻力系数影响较小，同时对于有限长发射管，附加质量还随航程增加而减小；

（4）移动网格数值仿真非常耗时，可以采用多机并行来加速求解，本文采用8个节点的多节点共享内存并行，可以获得最大加速比因子4.5。

本文数值仿真为AUV水下对接提供了数值仿真方法，同时数值仿真结果也为AUV水下对接工程提供了理论参考。

[1]Zhang L P,Yang Y J,Zhang H X.Numerical simulations of 3D inviscid/viscous flow fields of Cartesian/unstructured/prismatic hybrid grids[C]//Proceedings of the 4th Asian CFD Conference.Mianyang,China,2000.

[2]郭 正,刘 君,瞿章华.非结构动网格在三维可动边界问题中的应用[J].力学学报,2003,35(2):140-146.

[3]张来平,王振亚,杨永健.复杂外形的动态混合网格生成方法[J].空气动力学学报,2004,22(2):231-236.

[4]Mitsuhiro M Y,Kazuhiro N H.Unstructured dynamic mesh for large movement and deformation[C].AIAA,2002.

[5]夏 健,伍贻兆.基于混合网格的三维Navier-Stokes方程并行计算方法[J].航空学报,2005,26(3):290-293.

[6]Cavallo P A,Sinha N.Parallel unstructured mesh adaptation for transient moving body and aeropropulsive applications[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit.Reno,Nevada,AIAA,2004:1057-1067.

[7]Richard F H.The near-field flow and drag on cylindrical bodies moving concentrically inside very long tubes[R].NUSC,Newport Laboratory,1991:27-33.

[8]王燕飞,张振山,张 萌.自航发射鱼雷内弹道模型与仿真研究[J].系统仿真学报,2006,18(2):316-318,326.

Application of 3-D hybrid dynamic grids to simulate the flow in AUV swim-out

WU Li-hong1,2,FENG Xi-sheng1,HU Zhi-qiang1,2
(1 State key laboratory of Robotics,Shenyang Institute of Automation,Chinese Academy of Sciences,Shenyang 110016,China;2 Graduate School of the Chinese Academy of Sciences,Beijing 100049,China)

A 3-D hybrid dynamic grids method is presented to simulate moving boundary in Autonomous Underwater Vehicle(AUV)swim-out from bounded domain to unbounded domain.The 3-D hybrid grids are composed of prismatic/tetrahedral/hexahedral grids from inner to outer layer respecitvely.With AUV moving the prismatic grids move with AUV,while the hexahedral grids remain stationary.Meanwhile,the tetrahedral grids are deformed or re-meshed according to the motion of AUV.Results from the numerical simulation show that the pressure contour in AUV surface at different times,and the resistant coefficient of AUV at the whole sailing which agrees well with the theory are obtained.The relation between diameter ratio with AUV reistant coefficient and addmass coefficient in tube is also shown,which gives guide for AUV underwater docking to tube.

AUV;swim-out;3-D hybrid grids;dynamic unstructured grids;underwater docking

TP24

A

1007-7294（2010）07-0717-06

2009-04-29

机器人学国家重点实验室自主课题（RLZ200810）

吴利红（1978-），女，博士生，研究领域：水下机器人水动力分析，多体相对运动数值仿真。