θFXZ型测量机力变形误差分析
2010-06-07裘祖荣李醒飞向红标谭文斌赵成顺
陈 诚,裘祖荣,李醒飞,朱 嘉,向红标,谭文斌,赵成顺
θFXZ型测量机力变形误差分析
陈 诚,裘祖荣,李醒飞,朱 嘉,向红标,谭文斌,赵成顺
(天津大学精密测试技术及仪器国家重点实验室,天津 300072)
根据某θFXZ型特定结构测量机,研究其静力及动力变形误差的系统分析方法.在建立测量机非刚体数学模型的基础上,求解测量机由于力变形带来的测量误差值,并用激光干涉仪对测量机静力及动力状态下的误差分别进行了测量.利用所建立的数学模型对测量机存在的静力变形带来的测量误差进行补偿,使立柱在水平方向的偏摆带来的最大测量误差由补偿前的10.2.μm减小到1.0,μm.实验得到的动力状态变形结果可以用于测量机力变形误差补偿技术的进一步研究.
坐标测量机;力变形误差;非刚体模型;误差补偿
随着工业生产的发展,对坐标测量机的精度提出了越来越高的要求.单纯依靠提高测量机制作工艺、使用新材料来提高测量机精度,即使能够实现其目标,经济成本也会很高,因此误差补偿技术作为提高坐标测量精度的一个重要手段,得到了越来越广泛的应用[1].在研究测量机误差补偿的关键技术之前,分析其力变形引起的误差是一个重要环节.
坐标测量机实际结构和材料的特性使得测量机不可避免地存在静力和动力加速度引起的力变形误差[1-3].影响测量机力变形误差的主要因素有:①测量机各个部件存在相对运动时,其重力作用的变化使构件发生变形;②导轨联结处非刚性带来的构件偏摆;③动力加速度引起的变形等[4-5].
笔者基于θFXZ型[1]特定结构测量机,在准刚体模型基础上,建立其非刚体数学模型.系统地分析测量机力变形误差的来源,通过理论计算和有限元仿真得到其力变形误差值,最后使用双频激光干涉仪搭建实验系统以测量力变形误差,并对可以精确检定的力变形误差进行补偿.所研究的力变形误差分析方法对一般的坐标测量机也同样适用.
1 测量机的非刚体数学模型
所研究的测量机的结构如图1所示,共有4个做相对运动的部件.该测量机为θFXZ型[1]坐标测量机,由转台带动工件转动,立柱2做X方向移动,滑座3沿立柱2做Z方向移动.3个相对做直线运动的部件依靠滚动直线导轨副联结.

图1 θFXZ型坐标测量机Fig.1 Coordinate measuring machine with θFXZ structure
如图2所示,设滑座在立柱的高度为hz,由该机结构可以看出,由于立柱本身及立柱与底座间联结导轨副的非刚性变形,测头会在X方向产生位移误差.这表明测量机在X方向的测量误差是包括该变形的二元变量函数,需要建立非准刚体测量机数学模型.

图2 立柱非刚性变形情况Fig.2 Deformation of the non-rigid column
如图1所示,在底座、立柱与滑座上分别建立直角坐标系OXYZ、O1X1Y1Z1和O2X2Y2Z2.设在运动初始位置,3个坐标系的原点及X、Y、Z的方向重合[6].测量时,设测端在OXYZ坐标系中由点P(xp,yp,zp)分别沿X、Z方向移过x、z至点Q(xq,yq,zq),则测量误差Δx= xq-(x+xp),Δy= yq-yp,Δz= zq-(z+zp).
为了获得测量误差,需要求出点Q在OXYZ中的坐标(xq,yq,zq)[2],根据空间矢量转换关系,有

式中:1OO、12OO为坐标原点平移矢量;1-R为坐标旋转矩阵的逆矩阵;Δδ为力变形的附加位移;δx(x)为定位误差;δy(x)和δz(x)为Y、Z方向的直线度误差;εy(x,z)为引起立柱变形的附加转角;αxz为立柱和底座的垂直度误差;δx(x,z)和δz(x,z)均为引起立柱变形的X、Z方向附加位移.
将式(2)~式(5)代入式(1),且将式(1)右端展开,根据误差公式

可以得到

以上3式包含了测量机13项准刚体几何误差和由于力变形带来的附加误差.本文重点讨论力变形引起的误差Δδ.
2 测量机静力及动力状态分析
测量机力变形引起的误差较为复杂,需要分别分析静力和动力情况.为了方便分析计算,建立简化的力学模型.将测头及支架部分看作一个质量块D,其质量为mD、质心为oD,如图3所示.
2.1静力分析
将图3所示测头及支架部分进行简化,求出其综合质量及质心.
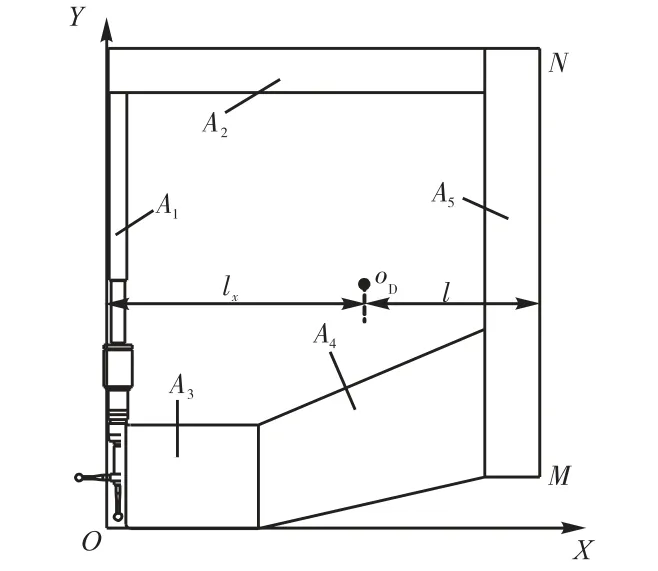
图3 测头及支架部分侧视图Fig.3 Side view of the probe and bracket
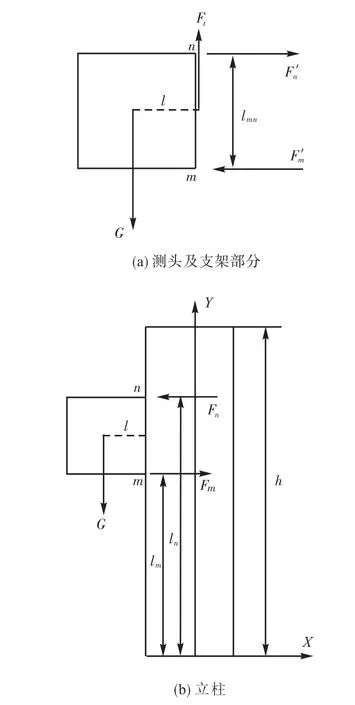
图4 测头及支架部分简化后立柱受力情况Fig.4 Force condition of the column after the simplification of probe and bracket
质量块D由Ai(i=1,2,3,4,5)5部分组成,其质心oD的求解方法为
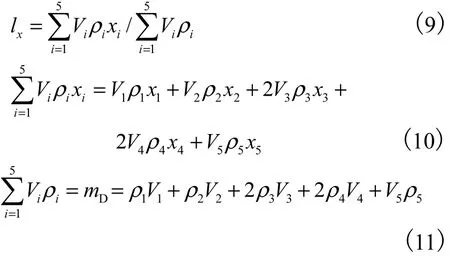
式中:lx为综合质心oD关于O点在X坐标方向的长度;Vi为各部分体积;ρi为各部分密度;xi为各自质心在X方向的坐标.
求得简化部分D后,首先将D从立柱分离出来单独分析受力,如图4(a)所示,以m为参考点,Ft为立柱对D施加的拉力,Fm΄和Fn΄是立柱对D施加的水平作用力.有
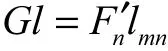
故

然后对立柱进行静力变形分析.D的重力G作用到m和n两点.根据力学平衡公式,D在X方向对立柱的作用力有2个:Fm和Fn. Fm、Fn和mF′、nF′是一对反作用力,如图4(b)所示.分别求解上述2个力对立柱n点在x方向变形的作用.Fn在点n作用,引起n点的挠度为
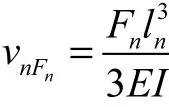
Fm在m点作用,在n点引起的挠度由挠曲线方程求解,即
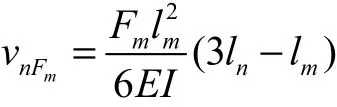
式中:E为材料弹性模量;I为立柱截面惯性矩.Fn和Fm对立柱的作用方向相反.由此求出静力状态下立柱变形引起的n点X方向偏移为

将测量机实际参数代入式(9)~式(11),求出mD为16.7,kg,lx为238,mm,l为72,mm.由式(12)求出Fn′和Fm′为±58N.最后由式(13)得到在静力状态下,由于D部分重力的作用,其在立柱不同高度hz处,立柱在X方向产生非刚性变形为0.3~4.5,μm;位置越高,其变形越大.
2.2 动力分析
机器运行时,驱动力作用于立柱下方,产生X方向的加速度a.立柱上端是没有任何约束的自由体,由于惯性力的作用,立柱上端会产生X方向的偏摆.D部分和立柱本身分别产生集中惯性力Fp和分布质量带来的均布惯性力q[7],如图5所示.

图5 立柱动态条件下受力分析Fig.5 Analysis of the column in dynamic situation
求解集中惯性力对立柱变形的作用.显然pF= -mDa ,设Fp在n、m两点的分力为P1和P2,P1=P2=.P1在n点作用,在n点引起的挠度为

P2在m点作用,在n点引起的挠度由挠曲线方程求解,即

综合P1和P2共同作用,集中惯性力在n点引起的挠度为

均布惯性力q在n点引起的挠度用均布载荷挠曲线方程求解,代入测量机参数,有

式中:s为立柱截面积;ρ为立柱材料密度;a为立柱水平运动加速度.
综合式(14)和式(15),求出立柱做水平运动时,惯性力使立柱产生的力变形误差,即在X方向上引起的挠度为

设仪器X轴方向速度为100,mm/s,加速度为100,mm/s2.通过式(16)可以求出D在Z轴hz处,产生的集中惯性力带来的立柱变形为0.16~2.3,μm,立柱的均布惯性力在不同的高度处引起的变形为0.2~2.9,μm.综合两力作用,D在立柱不同高度处,由于惯性力作用产生的X方向的变形为0.36~5.2,μm.
3 力学仿真及结果分析
运用有限元分析软件Ansys,建立测量机有限元模型进行数值仿真.模拟测量机立柱在静力条件下由于测头及支架部分重力以及立柱水平运动时动力作用产生的X方向变形.
图6(a)描述的是D部分在Z方向hz不同时,立柱在X方向产生的变形.结果显示,立柱在X方向的变形为0.5~4.7,μm.

图6 立柱变形有限元仿真结果Fig.6 Finite element analysis of the column deformation
动力状态仿真如图6(b)所示,给定立柱水平加速度为100,mm/s2,综合集中惯性力和均布惯性力的作用,当测头及支架部分hz变化时,立柱在X方向产生的变形为0.5~5.7,μm.
可以看出,仿真结果与计算结果很接近.
4 误差检定实验
采用HP双频激光干涉仪搭建实验系统,对上文分析和仿真的关于测量机在静力和动力状态下立柱变形进行测量,实验系统如图7所示.

图7 激光干涉仪测试实验系统Fig.7 Detection experiment system with laser interferometer
4.1静力条件下立柱变形
静力状态下,为了能够系统、准确地测量立柱在不同hz处相对安装在底座上光栅尺的水平方向偏移,将测量滑座X方向偏移的距离转化为测量立柱变形产生的绕Y轴的微小角度变化.角度反射镜随着滑座上下移动,位于立柱下端的角度干涉镜保持位置不变,保证不同高度处测量基准的一致.最后,将测量所得角度变化通过计算转化为滑座处X方向水平位移量即可.
基于所设计的实验系统,进行了15组相同条件下的实验,取实验数据的平均值进行处理,如图8所示.静力条件下,立柱非刚性变形带来的最大误差为10.2,μm,这个值比理论计算和仿真的数值大.原因在于,此误差不仅包含了引起立柱弯曲变形的附加位移δx(x,z),同时还包含了导轨联结处非刚性变形引起的附加转角εy(x,z).

图8 立柱及导轨滑块非刚性变形误差及补偿Fig.8 Error caused by deformation of the column and the joints and error compensation
需要注意的是,附加位移δx(x,z)和附加转角εy(x,z)在引起立柱结构的变形方面是存在差异的.附加位移δx(x,z)是一个关于测头及滑座部分在立柱上高度值的3次函数,其变形曲线可以根据实验测得的数据进行拟合.对于附加转角εy(x,z),这个角度变化体现在立柱底部的导轨联结处.本文研究的测量机由于测头及滑座部分重心偏离支撑中心轴,存在偏转力矩,所以会绕y轴产生角度偏转,也就是附加转角εy(x,z).在静力状态下,因为立柱的变形和偏摆幅度很小,当测头及滑座部分在立柱的上下位置不同时,对导轨联结处的作用力臂的变化可以忽略.因此附加转角εy(x,z)的值在静力状态下,测头滑座部分不同高度时,也是基本保持不变的.它对于立柱形变的作用就是要利用式(6)中zεy(x,z)来计算,在不同的高度z处,误差值不同;且随着滑座的升高和z值的增大,附加转角εy(x,z)引起的立柱在X方向的偏移值呈线性增大趋势.
为了将导轨联结处的非刚性变形带来的误差从立柱整体变形量中分离出来,设计实验,对滚动直线导轨副非刚性引起的立柱偏摆进行测量,实验原理如图9所示,在立柱底端加载质量块,其重力引起的扭矩大小与测头及支架部分引起的立柱扭转扭矩相等.
在hz高度,测量立柱的水平位移,可以得到由于滚动直线导轨副的非刚性引起的立柱偏摆.hz不同,偏摆误差值范围为0.2~4.7,μm.这个结果证明了导轨联结处的非刚性会带来力变形误差.
在实际情况中,立柱本身的弯曲变形和导轨联结处的非刚体变形是同时存在的,其综合作用如图8所示.根据实验结果,针对附加位移和转角综合引起的误差进行补偿,在静力条件下,可以将立柱复杂变形引起的测量误差减小到±1,μm以内.
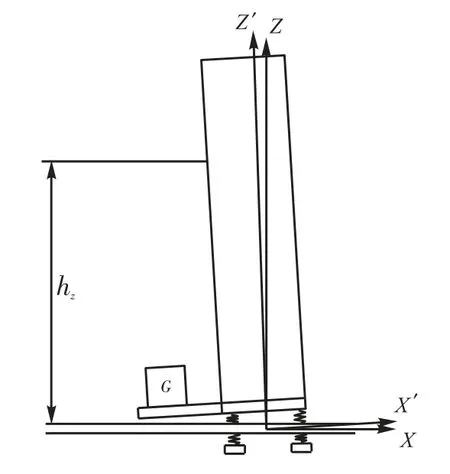
图9 滚动直线导轨副非刚性带来的立柱偏摆Fig.9 Error caused by deformation of the joints
4.2动力状态下立柱变形
动力状态下的立柱形变是一个随时间实时变化的动态量,相比静力变形,不易精确测量[8].针对动力加速度引起的力变形误差测量,设计了2组实验来观察其动力变形状态[9-10].第1组是D部分在立柱不同hz处,给立柱施加不同的水平加速度使其运动,观察D部分产生的集中惯性力在不同条件下对立柱变形的作用.第2组是D部分在立柱的hz位置固定,立柱水平运动时,用激光干涉仪测量D部分在X方向实时偏摆的位移值.
第1组实验的测量手段与静力测量实验相同,也是通过偏转角度的测量来实现位移测量.给定测量机立柱在X方向不同的加速度值,同时改变D的hz值,观察集中惯性力由于力臂的变化对立柱变形的影响.通过设计程序,让测量机立柱在X方向的两点之间做往复直线运动.在立柱运行的同时,激光干涉仪动态采集数据,每0.1,s采集1次.当立柱沿直线运动到换向时,立柱的偏摆角度最大,运用激光干涉仪软件的数据分析功能可以得到其不同条件下的最大角度值[11],通过计算将角度值转化为不同hz处立柱的偏摆位移.
实验结果如图10所示,图形显示了由于加速度和集中惯性力力臂的不同而引起的立柱动力变形误差变化趋势.

图10 加速度和hz不同的条件下立柱变形情况Fig.10 Deformation of the column with different motion parameters
第2组实验是将激光器升高至与D部分同样的高度,运用激光干涉仪测距原理测量D在X方向的实时力变形误差.设定运行速度为200,mm/s,加速度为150,mm/s2,立柱水平加速运行一段距离后停止,观察立柱在动力加速度作用下的力变形的动态特性.由图11可以看出,由于立柱本身惯性力和联结部分的非刚性,当立柱加速启动时,会产生延迟于运动方向的振动;当立柱运行停止时,立柱会在目标位置两侧来回振动,经过3,s左右时间,立柱才能相对静止.为了减小动力加速度引起的力变形对测量误差的影响,可以在立柱水平运行时尽量使D保持较低的位置,同时优化控制参数,减小启动和停止时的动力加速度.

图11 立柱动力状态特性Fig.11 Dynamic characteristics of the column
5 结 语
本文在建立特定结构测量机非刚体误差补偿模型的基础上,提出了系统分析静力及动力变形误差的方法.仿真和实验结果证明,该方法分离了静力和动力加速度带来的误差.将实验检测得到的静力变形误差,代入误差补偿模型,利用测量机软件进行补偿后,测头及支架部分在Z轴450,mm(200~650,mm)运行范围内,立柱在X方向的静力变形误差的最大值由补偿前的10.2,μm下降到1.0,μm.实验得到由动力加速度引起的立柱变形误差,相对静力变形误差更加复杂和难以精确检定.其主要来源是各个运动部件及其联结处的弱刚性引起构件本身的弹性弯曲和偏摆,以及测量机运动过程中由于各个构件惯性力引起的微小振动.可以通过改进测头运动路径、调整控制参数等手段减小测量机动力变形误差.该力变形误差分析、检定及补偿方法对一般的坐标测量机也同样适用.
[1] 张国雄. 三坐标测量机 [M]. 天津:天津大学出版社,1999.
Zhang Guoxiong. Coordinate Measuring Machine [M]. Tianjin:Tianjin University Press,1999 (in Chinese).
[2] Zhang G,Veale R,Charlton T,et al. Error compensation of coordinate measuring machines[J]. CIRP Annals,1985,34(1):445-448.
[3] 林述温,吴昭同,李 刚. 三坐标测量机非刚性效应测量误差分布特征[J]. 仪器仪表学报,2001,22(2):172-175.
Lin Shuwen,Wu Zhaotong,Li Gang. Volumetric distribution feature of measuring coordinate errors integrating with nonrigid errors [J]. Chinese Journal of Scientific Instrument,2001,22(2):172-175(in Chinese).
[4] 赵英剑,张国雄. 坐标测量机非刚体误差补偿模型中附加函数的研究[J]. 组合机床与自动化加工技术,1999(6):28-32.
Zhao Yingjian,Zhang Guoxiong. A study of additional functions in non-rigid body model for error compensation of CMMs [J]. Modular Machine Tool and Automatic Manufacturing Technique,1999(6):28-32(in Chinese).
[5] 董晨松,穆玉海,张国雄. 用激光干涉仪测量三坐标测量机的动态特性 [J]. 天津大学学报,1998,31(5):623-626.
Dong Chensong,Mu Yuhai,Zhang Guoxiong. Assessing the dynamic characteristics of CMMs with a laser interferometer [J]. Journal of Tianjin University,1998,31(5):623-626(in Chinese).
[6] Soons J A,Theuws F C,Schellekens P H. Modeling the errors of multi-axis machines:A general methodology [J]. Precision Engineering,1992,14(1):15.
[7] Sriyotha Pinet,Yamazaki Kazuo,Zhang Xingquan,et al. An experimental study on the vibration-free,high-speed operation of a three-dimensional coordinate measuring machine [J]. Journal of Manufacturing Systems,2004,23(3):173-181.
[8] Weekers W G,Schellekens P H J. Compensation for dynamic errors of coordinate measuring machines [J]. Measurement,1997,20(3):197-209.
[9] Castro H F F. Uncertainty analysis of a laser calibration system for evaluating the positioning accuracy of a numerically controlled axis of coordinate measuring machines and machine tools [J]. Precision Engineering,2008,32(2):106-113.
[10] Castro H F F,Burdekin M. Evaluation of the measurement uncertainty of a positional error calibrator based on a laser interferometer [J]. International Journal of Machine Tools and Manufacture,2005,45(3):285-291.
[11] Agilent Technologies,Inc. Agilent 5529A Dynamic Calibrator Measurement Guide [M]. USA:Agilent Technologies,Inc,2006.
Analysis of Force-Induced Errors of Measuring Machine with θFXZ Structure
CHEN Cheng,QIU Zu-rong,LI Xing-fei,ZHU Jia,XIANG Hong-biao,TAN Wen-bin,ZHAO Cheng-shun
(State Key Laboratory of Precision Measuring Technology and Instrument,Tianjin University,Tianjin 300072,China)
According to the structural characteristics of the coordinate measuring machine with θFXZ structure,a systematic analysis method of its errors induced by static and dynamic forces has been proposed. Based on the non-rigid body model of the measuring machine,its force-induced measuring errors were theoretically calculated and then measured with a laser interferometer under static deformation and dynamic deformation. Furthermore,with compensation of the measured error induced by static force using the mathematical model,the maximum error of the column deformation in X direction was reduced from 10.2 μm to 1.0 μm. Results of the dynamic deformation obtained from the experiment can be applied to further studiesof force-induced errors of the measuring machine.
coordinate measuring machine;force-induced error;non rigid body model;error compensation
TB92;TB93
A
0493-2137(2010)01-0064-07
2009-04-10;
2009-06-22.
国防预研基金资助项目(9140A0902210TJW1401).
陈 诚(1980— ),男,博士研究生,ccchina@163.com.
李醒飞,lixf@tju.edu.cn.
