基于遗传算法的混凝土湿度场特征参数求解及反分析

郭利霞，朱岳明，钟 锐，许 朴，钟 凌

(1. 河海大学水利水电工程学院，南京 210098；2. 河海大学水文水资源学院，南京 210098)

基于遗传算法的混凝土湿度场特征参数求解及反分析

郭利霞1，朱岳明1，钟 锐1，许 朴1，钟 凌2

(1. 河海大学水利水电工程学院，南京 210098；2. 河海大学水文水资源学院，南京 210098)

为了求解干燥环境中混凝土内部湿度分布，提出了利用遗传算法来求解混凝土湿度场特征参数．根据室内实验实测的湿度值，运用遗传算法对混凝土试块湿度场进行反演计算，得到反映混凝土湿度扩散性能的参数．利用这些参数和三维有限元仿真计算程序对湿度场进行分析，将计算值和实测值进行对比得知二者变化规律一致，各组数据相关系数大于0.98，说明利用反演的参数仿真计算是完全合理的，可以指导施工，同时说明遗传算法作为一种优化算法，具有收敛速度快、效果好等特点．

遗传算法；湿度；湿度扩散参数；反分析

在水利工程中，混凝土结构往往由于温度和湿度的变化而产生很大的拉应力，正是由于这个原因，在混凝土结构中会出现裂缝，严重危害到建筑物的安全，所以对混凝土结构来说温度裂缝和干缩裂缝的研究是具有重要意义的．相对于温度场及温度应力，混凝土湿度扩散及干缩应力的计算很复杂．虽然近年来人们对水分扩散和干缩应力的研究颇多，如Rahman[1-2]等通过实验进行了混凝土中干缩的有限元仿真分析，国内朱岳明和梁建文等[3-4]也就湿度变化而引起干缩应力进行了三维仿真分析，但是在实际工程中的应用还鲜见报道，其主要原因是湿度场计算的相关参数到目前来说还是很难确定的．笔者利用实验实测湿度数据，通过三维有限单元法和遗传算法对混凝土湿度场特征参数进行反分析，得到能反映混凝土扩散规律的湿度特征参数，用于工程实践．

1 计算原理与方法

1.1 湿度场计算

混凝土内部湿度变化主要取决于自干燥和水分扩散，其微分方程[5-7]可表示为

相应的初始条件为

在与空气接触的边界上，边界条件为

式中：h为相对湿度；Dx、Dy和Dz是湿度扩散系数，一般假设湿度扩散系数是各向同性的，表示为D(h)；hs为绝湿环境下水泥水化时消耗湿度；h0(x,y,z)为已知的相对湿度；β为表面湿度转移系数；ha为空气的相对湿度．利用变分原理，对式(1)采用空间域离散，时间域差分，引入初始条件和边界条件后，可得向后差分的湿度场有限元计算递推方程

式中：H为传导矩阵；R为传导补充矩阵；hn和hn+1为结点湿度列阵；Fn+1为结点湿度荷载列阵；n为时段序数；tΔn为时间步长．根据递推公式(4)，由已知上一时刻的结点计算湿度hn可以推出下一时刻的结点湿度hn+1．

1.1.1 水化反应消耗的湿度

拌合好的混凝土趋于饱和，即相对湿度可以看成是100%，但是水泥熟料矿物遇水后会发生水解或水化反应而变成水化物，这个过程称为自干燥，自干燥引起的湿度变化可以采用全密封同等条件养护试件测量[8]．该过程的湿度变化也可以借助于水泥的水化反应程度即水化度来表示，基本的水化度公式为

式中：()tα为龄期t时的水化度，当t →∞时，()tα→1；c()Wt为龄期t时累积参加水化反应的胶凝材料量，kg；cuW为最终参加水化反应的胶凝材料量，kg．由于单位质量胶凝材料水化反应的需水量不变，因此可采用水化耗水量来定义水化度

式中：()Gt为龄期t时的累积水化反应耗水量；uG为最终水化耗水量，表示成相对湿度变化形式为

式中：sG为饱和状态含水量；tG为总含水量．参考文献[9]中水泥水化热表达方式，本文自干燥中相对湿度的损失采用复合指数表示为

式中：sh∞为自干燥消耗的总的相对湿度；a和b为参数，随水泥品种、比表面积等不同而不同．

1.1.2 湿度扩散系数

扩散系数是扩散微分方程求解的重要参数，它的准确测定是湿度场计算的重要前提，不同文献取值不同[10-11]，根据CEB-FIP(90)[12]推荐模型，等温条件下，湿度扩散系数可表示成相对湿度的函 数，即

式中：01/mDD=，1D是()Dh的最大值，0D是()Dh的最小值；ch为最大湿度扩散系数降至一半时对应的相对湿度；n为指数．推荐使用m＝0.05，n＝15，ch＝0.8．

1.2 遗传算法基本理论

遗传算法是基于生物进化算法的一种，它主要借用生物进化过程中“适者生存”的规律，是一种智能化的全局搜索算法，可用来处理本文这种多参数、多变量的非线性优化问题，在给出决策变量编码后，计算过程简单且能较快地得到满意解，虽然要进行大规模的数值计算，但是如果选定较好的初始参数，收敛速度会很快．

1.2.1 编码

编码是应用遗传算法时要解决的首要问题，也是设计遗传算法时的1个关键步骤．本文采用浮点数编码方法，它是指个体的每个基因值用某一范围内的一个浮点数来表示，个体的码长度等于其决策变量的个数．

1.2.2 初始化过程

设n为初始种群数目，随机产生n个初始染色体．可先给定可行集Φ={(φ1,φ2,···,φm)|φk∈ [ak,bk], k=1,2,···,m}．其中，m为染色体基因数，也就是本文中反演分析参数的个数；[ak,bk]是向量(φ1,φ2,···,φm)第k维参变量φk的限制条件，再随机产生m个小于1的数xk,k∈[1,m]，初始染色体的第k个基因φk=ak+(bk−ak)xk,k∈[1,m]．重复上述过程n次，获取n个初始染色体V1,V2,···,Vn．

1.2.3 构造适应度函数

构造适应度函数是遗传算法的关键，应根据具体的问题构造合适的适应度评价函数，引导进化运算向最优解方向进行．本研究选择建立基于序的适应度评价函数，让染色体V1，V2，…，Vn按个体目标函数值的大小降序排列，使得适应性强的染色体被选择产生后代的概率更大．设α∈(0，1)，定义基于序的适应度评价函数

1.2.4 选择算子

采用回放式随机采样方式，以旋转赌轮n为基础，每次旋转都以建立的适应度评价函数为基础，为子代种群选择一个染色体．具体操作有如下4个步骤．

(1)计算累积概率PI，PI=pi，i=1,2,···,I,I ∈[1,n],P0=0.0；其中父代个体Vi被选择的概率pi为

(2)从区间(0，1)产生一个随机数θ；

(3)若θ∈(PI−1,PI]，则VI进入子代种群；

(4)重复步骤(2)～(3)n次，从而得到子代种群所需的n个染色体．

1.2.5 交叉算子和变异算子

交叉算子是遗传算法区别于其他进化计算的重要特征，在算法中起着关键作用，是产生新个体的主要方法．本文采用专门针对浮点制编码的算术交叉算子，该算子由2个个体的线性组合而产生2个新的个体．变异算子的主要作用是改善算法的局部搜索能力，维持种群的多样性，防止出现早熟现象，本研究采用非均匀算子进行种群变异运算，采用高斯变异，即在进行变异操作时，用符合均值为μ、方差为2σ的正态分布的一个随机数来替换原有基因值．具体操作有如下4个步骤．

(1)选择种群规模前5%的优良个体进行完全复制，进入子代种群；

(2)产生2个随机数ζi∈(0,1)，若ζi≤pc，则Vi与VM进行交叉操作．Vi=λVΜ+(1−λ)Vi；

(3)若ζi＞pc，则对Vi进行变异操作，随机产生12个在[0，1]上的数ri(i=1,2,···,12)，则

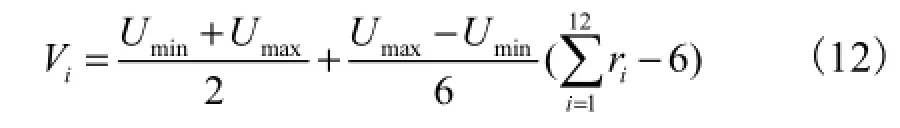
(4)重复步骤(2)～(3)n次，产生下一代种群所需的染色体．

初始种群产生以后，步骤(2)～(4)是上代种群产生下代种群进行的操作，程序的终止用进化代数或目标函数的设定值来判断，见文献[13]．

2 实验及湿度场反分析

2.1 实验情况

[14]中的实验，采用中强度和高强度2种混凝土，混凝土配合比见表1，试件尺寸为10,cm× 10,cm×20,cm，散湿面为10,cm×10,cm，其他5个面采用石蜡密封，测量的特征点A、B和C位于散湿面中轴线上(图1)，距离散湿面3,cm、7,cm和12,cm．混凝土试块浇注1,d拆模后放置在水中，3,d之后暴露在相对湿度(50±2)%、温度(20±2)℃的环境中．相对湿度的测量采用HMP44探头和HMI41指示器，在特征点位置钻孔后，置入塑料管，再在内部插入橡胶塞，橡胶塞中的相对湿度就由HMI41指示器进行测量，实验装置见图2，实验结果见表2和表3．

表1 混凝土配合比Tab.1 Mix proportions of concrete

图1 特征点分布Fig.1 Distribution of feature points

图2 内部湿度测定实验装置Fig.2 Measuring device for internal relative humidity in concrete

表2 中强度试块实测相对湿度Tab.2 Measured relative humidity of feature points in medium-strength concrete %

2.2 反演求解参数

根据实验浇注块原型建立有限元模型，网格剖分时采用空间六面体等参单元，计算的节点和单元数分别是1,089个和800个，在计算的过程中，石蜡密封的面视为绝湿面，暴露面按照第3类边界条件处理.

表3 高强度试块实测相对湿度Tab.3 Measured relative humidity of feature points in high-strength concrete %

根据浇筑现场3个特征点的实测湿度，对混凝土自干燥消耗相对湿度hs=hs∞(1−e−aτb)中的最终消耗湿度hs∞、反映湿度变化规律的a和b、湿度扩散系数D1以及混凝表面湿度转移系数β进行了反演分析．计算时取交叉概率为70%，变异概率为10%，系数α取0.1，目标优化函数取为

式中：i为测点序号；j为观测时刻；hij0和hij分别为实测和计算湿度值；m和n分别为测点数和测次数；ε是一个给定的很小的值．

经过15次的迭代求解，反演辨识的中强度混凝上的hs∞＝-0.15，参数a＝0.05，参数b＝0.79，β＝2.88×10−4m/d ，D1＝3.84×10−5m2/d ．13次迭代出高强度混凝上的hs∞＝-0.18，参数a＝0.055，参数b＝0.79，β=2.0×10−4m/d，D1＝3.48×10−5m2/d ．

2.3 结果比较及湿度场反分析

图3和图4为特征点相对湿度实测值和计算值对比图．可以看出，用混凝土反演参数计算的相对湿度值和实测值都随着时间地增长而减少，A点递减速度最快，B点次之，C点最慢，变化规律完全一致，且数值相差很小，相关系数为0.99，说明所得计算参数真实反映混凝土特性，利用遗传算法进行反演分析是可行且合理的．对比两图可以得知，早期高强度混凝土的相对湿度比同期中强度混凝土的相对湿度值要小，产生这种情况的主要原因是高强混凝土水灰比小，胶凝材料(水泥)用量多，水化反应消耗水分多．

图3 中强度混凝土试块各测点实测湿度与计算湿度比较Fig.3 Comparison between calculated relative humidity values and experimental values of medium-strength concrete

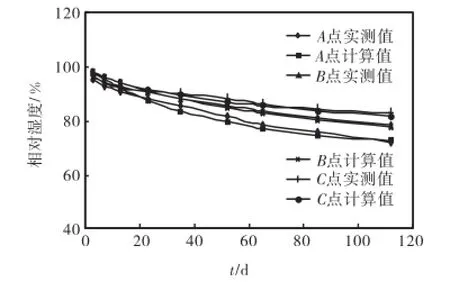
图4 高强度混凝土试块各测点实测湿度与计算湿度比较Fig.4 Comparison between calculated relative humidity values and experimental values of high-strength concrete

用反演得到的特征参数进行中强度混凝土试块湿度场仿真分析，整理出7,d和118,d的等值线分布图，见图5和图6．从图中可以看出，7,d时表层的湿度梯度是很大的，越往深处变化幅度越小，虽然这时混凝土弹性模量较小，但是表层湿度梯度大，而干缩应变随湿度的减小而增大[15]，应变大，内部湿度梯度小或几乎没有，应变较小，于是在表层产生很大的干缩应力，这也是干燥初期容易出现裂缝的主要原因．随着扩散时间的增长，到了118,d，表层的湿度梯度减小，同时也是越往深处梯度变化越小，但此时混凝土的弹性模量已经很大，也会产生较大的干缩应力，同时在实际工程中如果叠加了降温产生的拉应力，在基础的约束之下，是非常容易产生裂缝的，这些规律都已经在实际工程中得到了验证[16]．

图5 第7天湿度分布(单位：%)Fig.5 Moisture distribution on the 7th days(unit：%)

图6 第118天湿度分布 (单位：%)Fig.6 Moisture distribution on the 118th day(unit：%)

3 结 论

(1)根据室内实测的湿度值，对混凝土试块湿度场进行反演计算，并将计算值和实测值进行对比，分析计算结果跟实际情况相符，说明得到的参数可以反映混凝土湿度扩散规律，为实行防干缩措施提供理论依据．

(2)遗传算法在混凝土湿度参数反问题求解中具有精度高、反演快的优越性，克服了传统的梯度优化方法搜索速度随反演参数增多呈级数减慢、容易陷入局部极值点和误差传递导致不收敛等缺点，值得在工程中推广应用．

参考文献：

［1］ Rahman M K，Baluch M H. Simulation of shrinkage distress and creep relief in concrete repair[J]. Composites(Part B)：Engeering，2000，31(6/7)：541-553.

［2］ Oh B H，Cha S W. Nonlinear analysis of temperature and moisture distributions in early age concrete structures based on degree of hydration[J]. ACI Materials Journal，2003，100(5)：361-370.

［3］ 朱岳明，刘有志. 混凝土湿度和干缩变形及应力特性的细观模型分析[J]. 水利学报，2006，37(10)：1163-1168.

Zhu Yueming，Liu Youzhi. Analysis of concrete moisture dry shrinkage and stress based on mesoscopical model[J]. Journal of Hydraulic Engineering，2006，37(10)：1163-1168(in Chinese).

［4］ 梁建文，刘有志，曹为民，等. 水工薄壁混凝土结构湿度及干缩应力非线性有限元分析[J]. 水利水电技术，2007，38(7)：1163-1168.

Liang Jianwen，Liu Youzhi，Cao Weimin，et al. Nonlinear FEM analysis on moisture field and dry-shrinkage stress of thin-walled hydraulic concrete structure[J]. Water Resources and Hydropower Engineering，2007，38(7)：1163-1168(in Chinese).

［5］ Bazant Z P，Najjar L J. Nonlinear water diffusion in nonsaturated concrete[J]. Materials and Structures，1972，5(25)：3-20.

［6］ Kim J K，Lee C S. Prediction of differential drying shrinkage in concrete[J]. Cement and Concrete Research，1998，28(7)：985-994.

［7］ Jensen O M，Hansen P F. Autogenous deformation and RH change in perspective [J]. Cement and Concrete Research，2001，31(12)：1859-1865.

［8］ 晁鹏飞，郑建岚，王雪芳. 高性能混凝土水分扩散数值解法[J]. 福州大学学报，2007，35(6)：898-894.

Chao Pengfei，Zheng Jianlan，Wang Xuefang. Numerical algorithm for moisture diffusion in high performance concrete [J]. Journal of Fuzhou University，2007，35(6)：898-894(in Chinese).

［9］ 朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京：中国电力出版社，1999.

Zhu Bofang. Thermal Stresses and Temperature Control of Mass Concrete [M]. Beijing：China Electric Power Press，1999(in Chinese).

［10］ 张 君，侯东伟. 基于内部湿度试验的早龄期混凝土水分扩散系数求解[J]. 清华大学学报，2008，48(12)：2033-2035.

Zhang Jun，Hou Dongwei. Calculation of moisture diffusion coefficient in early age concrete from interior humidity tests[J]. J Tsinghua Univ，2008，48(12)：2033-2035(in Chinese).

［11］ 黄达海，刘光廷. 混凝土等温传湿过程的试验研究[J].水利学报，2002(6)：96-101.

Huang Dahai，Liu Guangting. Experimental study on moisture transfer in concrete under quasi-isothermal condition[J]. Journal of Hydraulic Engineering，2002(6)：96-101(in Chinese).

［12］ Comite Euro-International du Beton. CEB-FIP Model Code 1990 [S]. London：Thomas Telford，1993.

［13］ 周 明，孙树栋. 遗传算法原理及应用[M]. 北京：国防工业出版社，1999.

Zhou Ming，Sun Shudong. Genetic Algorithm Principle and Application [M]. Beijing：National Defense Industry Press，1999(in Chinese).

［14］ Kim Jin-Keun，Lee Chil-Sung. Moisture diffusion of concrete considering self-desiccation at early ages[J]. Cement and Concrete Research，1999，29(12)：1921-1927.

［15］ Bazant Z P. Creep and Shrinkage of Concrete[D]. Michigan：Department of Civil Engineering，Northwestern University，2000：1-83.

［16］ 王星梅. 大型泵站防裂技术研究与实践[D]. 南京：河海大学水利水电工程学院，2005：59-60.

Wang Xingmei. Study and Practice on the Concrete Crack Prevention of the Large Pumping Station[D]. Nanjing：College of Water Conservancy and Hydroelectric Engineering，Hohai University，2005：59-60(in Chinese).

Solution of Concrete Moisture Diffusion Parameters Based on Genetic Algorithms and Back Analysis

GUO Li-xia1，ZHU Yue-ming1，ZHONG Rui1，XU Pu1，ZHONG Ling2
(1. College of Water Conservancy and Hydroelectric Engineering，Hohai University，Nanjing 210098，China；2. College of Hydrology and Water Resources，Hohai University，Nanjing 210098，China)

To obtain moisture distribution of concrete exposed to dry air，genetic algorithms were proposed to calculate moisture diffusion parameters. Based on the measured relative humidity, relevant parameters were obtainedby inverse analysis. With those parameters and 3-D FEM, the long-term distribution of relative humidity was gained. From the result, it is known that the calculated values agree well with the experimental values. The correlation coefficient R of all statistics is higher than 0.98，which indicates that simulation analysis using inversion parameters is quite reasonable and can be applied to guiding construction．Meanwhile，as one of optimization methods，genetic algorithms are simple and highly efficient.

genetic algorithms；humidity；parameters of moisture diffusion；back analysis

TV315

A

0493-2137(2010)08-0712-05

2009-04-10；

2009-09-09.

国家自然科学基金资助项目(50779010，50539010).

郭利霞（1982— ），女，博士研究生，guolx@126.com.

朱岳明，hhuzym@126.com.