一种二平动自由度并联机械手动力尺度综合
2010-06-05张利敏梅江平赵学满
张利敏,梅江平,赵学满,黄 田
(天津大学机械工程学院,天津 300072)
一种二平动自由度并联机械手动力尺度综合
张利敏,梅江平,赵学满,黄 田
(天津大学机械工程学院,天津 300072)
研究一种二平动自由度高速并联机械手的动力尺度综合方法.在建立逆刚体动力学模型基础上,提出一种基于单轴最大驱动力矩全域最大值最小的动力学性能评价指标,该指标可表示为系统尺度和惯性参数及位形的显函数形式,可直接用于观察奇异位形的出现条件.建立雅可比矩阵奇异值的显式,提出一组兼顾速度、精度和刚度的传递角约束方程,通过考察奇异值与运动学性能的关系,可将传递角约束方程转化为性能约束方程,同时配以工作空间/机构尺度等约束条件,利用工程实例研究性能约束对尺度参数和动力学性能评价指标的影响规律,由此综合出在满足上述约束条件下使得系统动力学性能最优的尺度参数.
并联机械手;动力性能;尺度综合
目前,高速并联机械手已在电子、食品和医药等领域中得到应用,完成对轻小物料的高速分拣、插装、封装和包装等操作.此类机械手因含外转动副驱动、平行四边形支链,且可将驱动器布置在机架上及将运动部件做成轻杆,故可获得很高的速度和加速度,其典型代表包括三平动自由度Delta[1]机械手,以及三平动、一转动四自由度H4[2]机械手等.然而,对于仅需在一个平面内完成高速运动的场合,采用二自由度高速并联机械手在成本控制上较Delta和H4机械手更为适宜,因此同样具有重要的实用价值.
尺度综合是上述高速并联机械手设计的重要环节.目前采用的主要方法是将雅可比的代数特征(如条件数、奇异值、行列式等)作为系统局部性能的评价指标[3-8],且将其全域数字特性(极值、均值、波动量及其组合)作为优化设计的目标函数[9-10].此外,利用可以定量衡量机器人功率输入与输出有效性的传动性能指标[11]也被引入到尺度综合当中,对于平面并联机构,可利用平面传动角来评价传动性能的优劣[12].值得注意的是,上述优化指标以及雅可比代数特征的多样性往往导致优化结果并不唯一.
上述问题已引起许多学者的广泛关注.Hao和Merlet[13]以Stewart平台为例,采用区间分析法提出一种并联机构的尺度综合方法.该方法综合考虑了精度、刚度、工作空间/机构体积等指标的许用区间,进而试图得到可同时满足相关性能要求的尺度参数区间.Liu等[14]利用性能图谱在若干并联机构全域速度、力、伺服刚度传递特性与无量纲尺度参数间关系的基础上,提出一种尺度参数的综合方法.显然,上述工作的目的就是要在综合考虑多种性能指标的基础上,解决尺度综合结果的不唯一性问题.此外,由于机构做高速运动时必须计入运动构件惯性的影响,故还可利用惯性矩阵的代数特征构造相应的刚体动力学性能指标[15].然而值得指出的是,同时兼顾运动学和刚体动力学的尺度综合方法还鲜见报道.
笔者以一种天津大学发明的二平动自由度高速并联机器人机构——Diamond机构[5]为对象,在建立其运动学和刚体动力学模型的基础上,研究可同时兼顾运动学和刚体动力学的尺度综合方法.其基本思路是以单轴驱动力矩全域最大值最小为目标,通过考察关节空间与操作空间的速度、精度、刚度映射与雅可比奇异值之间的内在联系,提出一组满足上述性能的约束方程,同时配以工作空间/机构尺度等约束条件实现机构尺度参数的优化设计.
1 Diamond机械手刚体动力学模型
如图1所示,Diamond机械手由静平台,2条支链和动平台组成,所有运动副均为转动副.各支链包含与肘架相连的2组平行四边形,进而使动平台始终保持与静平台呈固定姿态.在安装于静平台且前端带有行星减速器的伺服电机驱动下,两主动臂可做独立转动,进而使得动平台在运动平面内做二自由度平动.为了降低运动部件的惯性,机构中的主动臂和从动臂采用碳纤维,而肘架和动平台采用铝合金制成.

图1 Diamond二平动高速并联机械手Fig.1 2-DOF translational parallel manipulator Diamond
考虑到平行四边形支链中的两平行杆件运动相同,故可将原系统简化为如图2所示的二自由度平面5杆铰接机构,其中动平台被视为质点.建立如图2所示参考坐标系O-xy,则动平台参考点O′在该系下的位矢r=(xy )T为

式中:1l、2l、iu和iw分别表示支链i中主、从动臂杆长和单位矢量;e表示两主动臂轴线间距与动平台内侧两铰点间距之差的一半,上述矢量可表示为


图2 二平动高速并联机械手运动模型Fig.2 Kinematic model of 2-DOF translational parallel manipulator
根据装配模式,经推导可得到该机构的位置逆解模型为

据此,可确定iu,wi计算式为
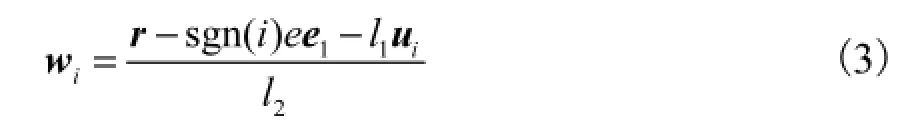
将式(1)关于时间求导,得
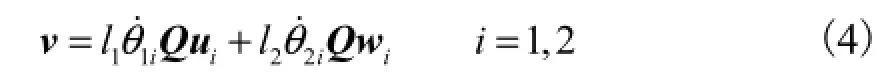
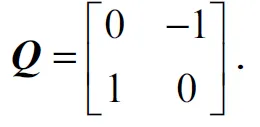
将式(4)两端同点积iw写成矩阵形式,有

式中J为机构的速度雅可比矩阵,表示为

将式(4)关于时间求导,得

将速度分析的结果代入式(6),得

式中:a为点O′的加速度矢量;θ˙1i为支链i中主动臂的角加速度,=()T;f(v)可表示为

建立系统逆动力学模型时,利用了如下3点假设:①运动副为理想的,即无摩擦引起的能量耗散;②因从动臂采用轻质细杆,忽略其转动惯量,而将其质量按静力等效原则简化到两端;③因动平台作平动,故将末端执行器和负载的质量折算到O′.
由虚功原理得

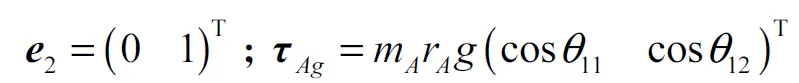
将δθ1=Jδr,=Ja+f(v) 代入式(8),可得系统的逆动力学方程
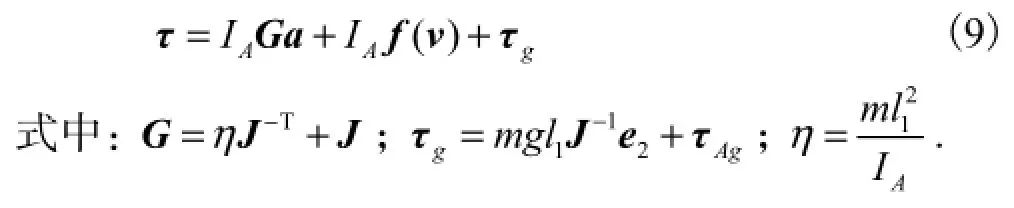
2 Diamond机械手动力尺度优化
2.1 工作空间及设计变量
如图3所示,当给定H、l1、l2和e后,点O′的可达空间W为主动臂到达上、下角极限时,以点Bi′和为圆心,以l2为半径四段圆弧所围区域.考虑到机械手做“抓放”操作(pick-and-place)时,一般在一宽/高比较大的矩形区域内运动,为此在W内剪裁出一个宽为b,高为h的矩形,其顶边与W的上边界切于点P1和P2,而下角点Q1、Q2恰在W的下边界上.在此定义该矩形为机械手的设计空间Wt.考虑到工程实际需求,在此取0.15≤hb ≤0.2.

图3 机构工作空间Fig.3 Workspace of 2-DOF parallel robot
为了便于讨论尺度参数对性能指标的影响,用1l对e、H和2l归一化处理,即

2.2 动力学性能评价指标
以往研究表明,加、减速阶段的惯性力矩在整个负载力矩中占有主导地位.因此,在计算峰值力矩时可略去式(9)中的重力项与哥氏力项,而将系统的逆动力学方程近似表示为

据此,Diamond机械手的单轴驱动力矩为

式中iG表示G的第i行的行向量,且

利用矩阵奇异值分解原理,易证实现点O′单位加速度所需的机械手单轴最大驱动力矩为
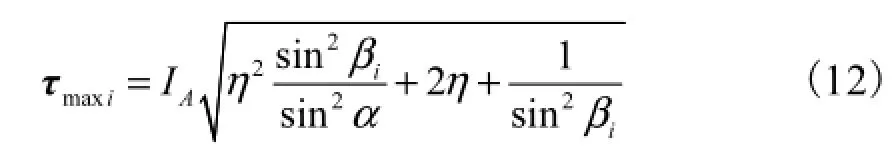

由式(12)显见,Diamond机械手的单轴最大驱动力矩为尺度参数、惯性参数及点O′位置的函数;若α→0或βi→0或二者同时成立,都会因机械手趋向直接或间接奇异,导致τmaxi→∞.因此,考虑到结构轴对称性,可将任一τmaxi的全域最大值最小作为动力学性能的优化目标,即
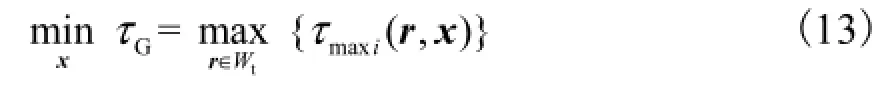
式中:r表示点O′的位置矢量;x=(λeλHλl)表示设计参数的集合.
2.3 约束条件
在确定性能评价指标后,还需要考虑机械手受到的尺度约束和性能约束.
2.3.1 尺度约束
考虑到在机架上应留有足够空间安装2个伺服电机,因此

此外,为了在保证性能的同时使机械手相对于给定的工作空间尽量紧凑,选定工作空间与机构尺度比为

2.3.2 性能约束
速度、精度和刚度是评价机械手性能的重要指标,因此在设计过程中将作为性能约束加以考虑.通过考察关节空间与操作空间的速度、精度、刚度映射可见,刚度与精度性能最终反应在min()σJ上是一致的,为提高刚度与精度性能应使得雅可比矩阵的最小奇异值最大,即

而速度与精度性能相互矛盾,若使点O′运动速度最快应使得雅可比矩阵的最大奇异值最小,即
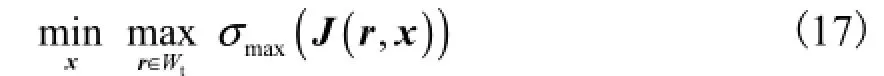
对于本文研究的二自由度平面并联机构,易得出速度雅可比矩阵的奇异值显示表达,即

由式(18)可见,速度雅可比矩阵奇异值是机构传动角α和βi的显函数,若α→0或βi→0,从而产生直接或间接奇异,导致σmin(J)→0或σmax(J)→∞,此时速度特性或精度特性将丧失.因此,若兼顾速度与精度特性,则需给定传动角α和βi的取值范围,即α∈[θT,90°],βi∈[θF,90°].
故可构造如下性能约束方程

3 算例与讨论
通过一个算例来揭示出性能约束对尺度参数,及尺度参数对性能评价指标的影响规律,并以此为依据综合出一组可获较好综合性能的尺度参数.
给定Diamond高速并联机械手的工作空间为宽b=800 mm ,高h=120 mm的矩形.注意到系统中主动臂的转动惯量和从动臂的等效质量为杆长的函数,故设主动臂中间段为等截面,并令μ1、μ2分别为主动臂和从动臂中间段单位长度的质量,md为主动臂远轴端及肘架的质量和.由此得到的相关惯性参数与杆长的关系如表1和表2所示,其中md=0.42 kg,μ1=0.848 g/mm ,μ2=0.0674 g/mm.

表1 折算到主动关节的转动惯量Tab.1 Equivalent moments of inertia of active proximal link (kg·m2)

表2 动平台集中质量Tab.2 Equivalent mass of moving platform kg
图4示出了eλ为0.2、0.25和0.3时,Gτ随Hλ和lλ的变化规律.由图可见,Gτ随eλ地增大单调减小.对于给定的eλ,Gτ随着Hλ和lλ地增大逐渐增大,且呈对折分布,即存在一组呈近似线性的Hλ、lλ偶对,使得Gτ取得局部最小值.
图5和图6示出了给定λe=0.3时,σmin和σmax随λH和λl的变化规律.由图可见,当取bl=0.6、0.7和0.8,bu=1.4、1.7和2.0时,将形成不同的约束面,由此限制了λH和λl的取值范围.由图5可见,σmin随λH增加单调增加,且随λl增加单调减少.当增大bl,即随着对精度要求的提高,λl和λH的可行域均减小,但前者首先达到可行域边界.又如图6可见,σmax随λH和λl的分布与τG随λH和λl的变化相似,亦呈对折曲面状.当减小bu,即随着对速度要求的提高,λl和λH的可行域均减小,但后者首先达到可行域边界.显然,若给定的性能约束使得λH和λl的可行域为空,则不存在满足给定性能约束的尺度参数解答.
图7示出了λe和[blbu]对τG最优值的影响规律.由图可见,在λH和λl可行域中的解与λe的大小及区间[blbu]的大小和位置有关.主要表现为区间[blbu]右移时,将收敛到λl的可行域边界;当[blbu]左移时,将收敛到λH的可行域边界.此外,缩小区间范围及增大λe都将缩小λH和λl的可行域.例如,当λe=0.7时,仅在区间[0.71.6]上存在唯一λH和λl偶对使得τG取得极小值.
为了进一步说明优化设计流程,选定性能约束区间[0.6 1.5].参见图7,当将λe增大到λe=0.6时有=0.3914 N·m ,且收敛于λH的可行域边界.由图8示出的τG随λH和λl的变化规律可见,对应=0.3914 N·m 的无量纲尺度偶对为λt=2.56和λH=1.97.据此,经比例换算和圆整可得到一组尺度参数:e*=150 mm,=250 mm,=640 mm,H*= 493 mm.
由以上算例可见,在满足速度、精度和刚度约束条件下,所优化的尺度参数可使主动关节力矩达到最小值,因此可指导伺服电机的选用,以便达到降低能耗的目的.

图4 τG随eλ、Hλ和lλ的变化规律Fig.4 Variation of τGversuseλ,Hλandlλ

图5 minσmin随λH、λl和bl的变化规律(λe=0.3)Fig.5 Variation of minσminversusλH,λlandbl(λe=0.3)

图6 maxσmax随λH、λl和bu的变化规律(λe=0.3)Fig.6 Variation of maxσmaxversusλH,λlandbu(λe=0.3)

图7 随λe和性能约束[blbu]的变化规律Fig.7 Variation ofversus λeand [blbu]

图8 τG随lλ和Hλ的变化规律Fig.8 Variation of τGversuslλandHλ
4 结 论
(1)Diamond机械手的单轴最大驱动力矩可表示成系尺度参数、惯性参数、主动臂与从动臂间夹角,及从动臂彼此间夹角的显函数,出现直接或间接奇异位形时均将导致单轴驱动力矩趋于无穷,因此将其全域最大值Gτ最小作为系统的动力学性能指标是合理的.对于给定的eλ,存在一组呈近似线性的Hλ、lλ偶对,使得Gτ取得局部最小值.
(2)通过速度雅可比矩阵最大及最小奇异值的显式表达,揭示传动角的取值范围可影响机构速度与精度、刚度特性,据此提出一组兼顾速度与精度特性的性能约束,并在该约束条件下,得到一组使得系统全域动力学性能最优的尺度参数.
[1] Clavel R. Device for the movement and positionning of an element in space:USA,US 4976582[P]. 1990-12-11.
[2] Pierrot F,Company O. H4:a new family of 4-DOF parallel robots[C]// Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics. New York,1999:508-513.
[3] Gosselin C M,Angeles J. The optimum kinematic design of a spherical 3-DOF parallel manipulator[J]. ASME Journal of Mechanism,Transmission,and Automation in Design,1989,111(2):202-207.
[4] Zanganeh K,Angeles J. Kinematic isotropy and the optimum design of parallel manipulators [J]. Int J Robot Res,1997,6(2):185-197.
[5] Huang Tian,Whitehouse D J,Wang Jinsong. Local dexterity,optimum architecture and design criteria of parallel machine tools[J]. CIRP Ann ,1998,47(1):347-351.
[6] Liu Xinjun,Jin Zhenlin,Gao Feng. Optimum design of 3-DOF spherical parallel manipulators with respect to the conditioning and stiffness indices[J]. Mechanism and Machine Theory,2000,35(9):1257-1267.
[7] Kim H S,Tsai L W. Design optimization of a cartesian parallel manipulator[J]. ASME Journal of Mechanical Design,2003,125(3):43-51.
[8] Ryu J,Cha J. Optimal architecture design of parallel manipulators for best accuracy[C]// Proceedings of 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. New York,2001:1281-1286.
[9] Gosselin C M,Angeles J. A globe performance index for the kinematic optimization of robotic manipulators[J]. ASME Journal of Mechanical Design,1991,113(3):220-226.
[10] Huang Tian,Li Zhanxian,Li Meng. Conceptual design and dimensional synthesis of a novel 2-DOF translational parallel robot for pick-and-place operations[J]. ASME Journal of Mechanical Design,2004,126(5):449-455.
[11] Chang W T,Lin C C,Lee J J. Force transmissibility performance of parallel manipulators[J]. Journal of Robotic Systems,2003,20(11):659-670.
[12] Liu Xinjian,Wu Chao,Wang Jinsong. A new index for the performance evaluation of parallel manipulators:A study on planar parallel manipulators[C]// Proceedings of the 7th World Congress on Intelligent Control and Automation. New York,2008:353-357.
[13] Hao F,Merlet J P. Multi-criteria optimal design of parallel manipulators based on interval analysis[J]. Mechanism and Machine Theory,2005,40(2):157-171.
[14] Liu Xinjun,Wang Jinsong,Pritschow G. Performance atlases and optimum design of planar 5R symmetrical parallel mechanisms[J]. Mechanism and Machine Theory,2006,41(2):119-144.
[15] Yoshikawa T. Dynamic manipulability of robot manipulators[J]. Journal of Robotic Systems,1985,2(1):113-124.
Dynamic Dimensional Synthesis of a 2-DOF Translational Parallel Manipulator for Pick-and-Place Operations
ZHANG Li-min,MEI Jiang-ping,ZHAO Xue-man,HUANG Tian
(School of Mechanical Engineering,Tianjin University,Tianjin 300072,China)
An approach was proposed for the dynamic dimensional synthesis of a 2-DOF translational parallel manipulator for pick-and-place operations. On the basis of rigid body dynamic formulation,a global dynamic performance index was proposed to minimize the maximum driving torque of a single active joint. The proposed index can be explicitly expressed in terms of dimensional and inertial parameters as well as system configurations,allowing the singular configurations to be easily found. By establishing the explicit singular value of Jacobian matrix,a set of the transmission angle constraints taking into account mapping characteristics of speed,accuracy and rigidity were proposed.Then the transmission angle constraints were transformed into a set of performance constraints by investigating the relationship between singular value and kinematics performance.Simultaneously,workspace/machine volume ratio was taken into account.Through an example,the effects of the performance constraints on the feasible domains of design variables and the performance index were discussed in depth.A set of optimized dimensional parameters were obtained for achieving a comprehensive performance throughout the entire workspace.
parallel manipulator;dynamic performance;dimensional synthesis
TH122
A
0493-2137(2010)08-0661-06
2009-03-26;
2009-06-02.
国家高技术研究发展计划(863计划)资助项目(2007AA04Z245);国家自然科学基金资助项目(50675151);教育部博士点基金资助项目(20060056018).
张利敏(1983— ),男,博士研究生,tju.zlmwan@yahoo.com.cn.
黄 田,htiantju@public.tptp.tj.cn.
