一种支持ANSI编码的中文文本压缩算法
2010-06-05常为领方滨兴云晓春王树鹏余翔湛
常为领,方滨兴,,云晓春,王树鹏,余翔湛
(1. 哈尔滨工业大学 计算机网络与信息安全技术研究中心,黑龙江 哈尔滨 150001;2. 中国科学院 计算技术研究所,北京 100190)
1 引言
数据压缩是指在一定的数据存储空间要求下,将相对庞大的原始数据,重组为满足前述空间要求的数据集合,使得从该数据集合中恢复出来的信息能够与原始数据相一致,或者能够获得与原始数据一样的使用品质。数据之所以能得到压缩的原因在于数据中存在冗余及数据所表示的信息之间存在关联。数据压缩减少了数据存储所需要的空间,从而间接减少了处理数据所需要的时间及资源耗费。
编码是信息处理的基础,不同国家和地区存在着不同的编码标准,主要为单字节编码和多字节编码两种。印欧语系主要采用ASCII编码。汉字数量巨大,必须采用多字节编码才能表示,表示汉语的编码主要包括GB2312-80、GBK、Unicode编码、GB18030-2000、BIG5等编码。
压缩算法的研究及开创性的工作是由西方国家完成的,因此,几乎所有数据压缩算法的实现都是基于单字节的,这些基于单字节的数据压缩算法,在处理多字节编码的数据时,人为地割裂了数据编码中蕴含的语义信息,严重地损害了压缩率。对于基于ASCII的单字节英文文本,现有的压缩工具已经达到0.8bpc (bits per char/byte)左右的压缩率,而对于中文文本仅能达到3.0bpc左右,远远低于英语文本。因此需要针对中文语言,充分考虑其在编码、语义方面的特点,研究相应的压缩算法。
数据压缩技术分为无损压缩和有损压缩两大类,无损压缩技术通常又分为基于统计的压缩技术及基于字典的压缩技术。基于统计的压缩技术根据字符在数据流中的出现概率对其进行编码,经常出现的字符分配较短的编码,不常出现的字符分配较长的编码,代表性技术有Huffman编码、算术编码及PPM等。基于字典的压缩技术将数据流中已经出现的字符及字符串放入一字典中,对于重复出现的字符及字符串用指向字典中该字符串的指针来表示,由于指针的长度小于所代替的字符或字符串长度,所以能起到压缩的效果,代表性技术有LZ77、LZ78等等。
传统的Huffman编码[1]根据字符出现的频率构造编码,是基于ASCII字符的(character-based),在编码过程中并没有产生信息熵的转移,其对自然语言文本的压缩效果是有限的,因此通常作为其他压缩算法的后端模块或补充。当将Huffman编码扩展到基于多个字符时,如基于词(word-based)或基于音节(syllable-based)时,Huffman编码的压缩率会大幅度提高,这是因为多个字符的组合造成的概率分布不均衡要比单个字符要大,从而可能获得更大的压缩率。对于英文文本,基于字符的Huffman编码的压缩比能达到1.7左右,而基于单词的Huffman编码能达到4倍左右的压缩比[2],达到或接近LZ的压缩效果。基于词的Huffman编码不仅能提高压缩率,同时,由于其在压缩过程中保留了字/词的语义完整性,不像传统Huffman编码方法将文本分为一个个字节,人为地割裂了文本中单词的语义,因而在压缩文本的检索方面可能效果更好,速度更快。MG[3]系统就应用了基于单词的Huffman编码。
LZ[4-7]系列算法通过使用编码器中已经出现过的相应匹配数据信息替换当前数据从而实现压缩功能。但是,根据词频统计显示,汉语文本中单字词与双字词占绝对多数,因此,汉语文本中重复子串不可能很长[8],从而使LZ系列算法在中文文本上的压缩性能大打折扣。尽管LZ系列算法还包括LZ78[5]及LZW[7],由于LZW的专利权限制,LZW的使用受到相当大的制约,但LZSS[6]就没有这些约束,从而更受到各种应用的青睐,如LZSSCH[9]等。
PPM[10-11]维护一统计模型,该模型根据字符组合预测下一个字符出现的概率,并由算术编码对该概率进行编码输出。近年来,对PPM算法的研究主要集中在PPM的概率的预测模型或PPM的阶数上,而对基于多字节的PPM算法研究成果很少。Joaquín Adiego和Pablo de la Fuente[12]采用对文本中的单词进行重新编码及将PPM改进为基于字/词的PPM,大大提高了PPM的性能。Peiliang Wu和W. J. Teahan[13]将PPM字符压缩的基本单元由8bits扩展到16bits,获得了4%~10%的压缩率的提升。
BWT[14]是按块批量处理数据,其核心思想是先对字符串轮转后得到的字符矩阵进行排序和变换,然后对变换之后的字符串用MTF变换或RLE进行处理,最后使用Huffman或算术编码进行编码。对于英文文本,BWT算法的压缩效果要远好于LZ系列算法,但对于中文文本,考虑到中文编码的特殊性及中文语义、语法方面与印欧语系的巨大差异,还需要对BWT算法在中文文本的压缩技术中的适应性进行深入研究。
2 数据流的语义特征
本文将数据流定义为以bit或byte为基本单位的二进制序列。
在压缩算法中,数据流呈现出两种特性,一是物理特性,如某种bit或byte值的概率分布、byte值的排列顺序、某些bit或byte串在数据流上下文中的重复等等;另一种是语义特征,包括两方面的含义,一是通过物理特性体现出来的语义信息,如字节值的排列顺序不同或由多个字节的组合来表示不同的字符,本质上是编码之间的相互依赖关系。另一种是产生数据流的应用本身所蕴含的语义,基于此种含义,有的学者认为数据压缩是一个AI-Hard[15]问题。本文所讨论的语义特征,主要是指通过物理特性体现出来的语义信息。
数据压缩本质上是一个可逆的编码过程,数据流的语义特征与编码方式息息相关,如文本:“科学院南路2号计算所ICT。”,其利用编码蕴含语义的方式有以下几种:
1) 以字节为单位的变长编码方式
如采用ANSI编码,即双字节编码方式,上述文本编码为:“BF C6 D1 A7 D4 BA C4 CF C2 B7 32 BA C5 BC C6 CB E3 CB F9 49 43 54 A1 A3”,其中,中文字符及标点符号占16bit,数字和英文字符占8bit,其在字节值、字节顺序及字节组合中所蕴含的语义信息如图1,其中上图为原数据流编码,下图为对应编码所代表的语义,可以看出,该段数据流为双单字节相间的二进制序列,其字节值、字节的排列顺序及两个字节的组合是一定的,不可以随意更改,否则将改变所蕴含的语义信息。

图1 原数据流的编码与语义信息
或者采用混合编码方式,即某些中文字符与数字、英文字符用8bit,其他用16bit或24bit进行编码, 维持原排列顺序,如图2。

图2 压缩编码方式与语义信息示例:混合编码
2) 以字节为单位的定长编码方式
图3中,每个字符由一个字节表示,且编码的排列顺序与原文本中的字符顺序相同,如果使用基于单字节的压缩算法进行压缩,在进行概率计算、字符比较时能充分利用所蕴含的语义信息,可获得最优的压缩性能。
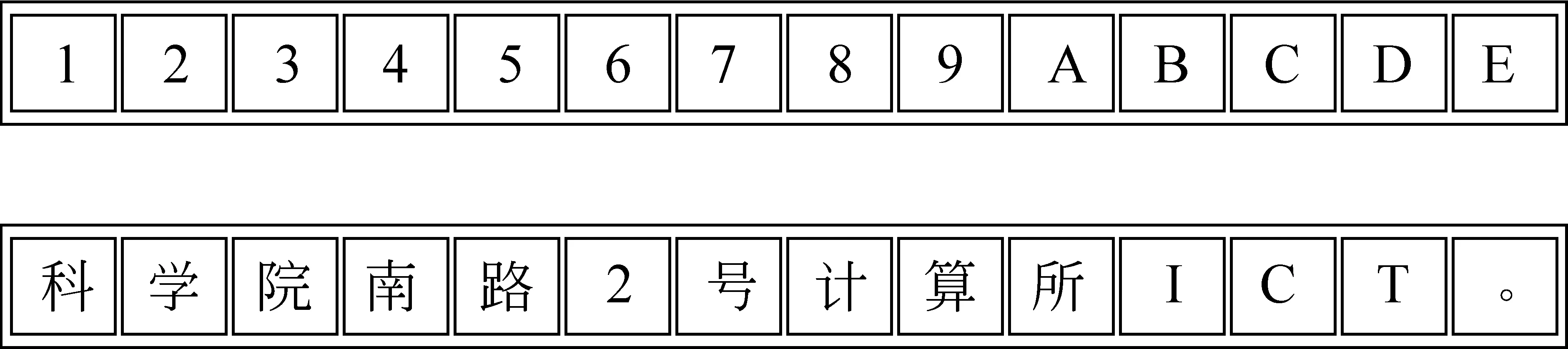
图3 压缩编码方式与语义信息示例:单字节编码
3) 以位为单位的变长编码方式
此类编码方式以Huffman编码为代表,其根据概率的不同分别对字符分配以不同位长的编码。
根据压缩算法对数据中语义信息的维持效果,可以将压缩算法分为维持语义的压缩算法及打乱语义的压缩算法。这里语义是指以位(单个bit)或位的组合(多个bit)所表示的具有明确含义的编码信息及编码之间的相互依赖关系。压缩算法本质上是一种信息的再编码过程,维持语义的压缩算法是指压缩后的数据流依然保持了原数据流中编码本身的独立关系(单个或多个bit)及编码之间的相互依赖关系。
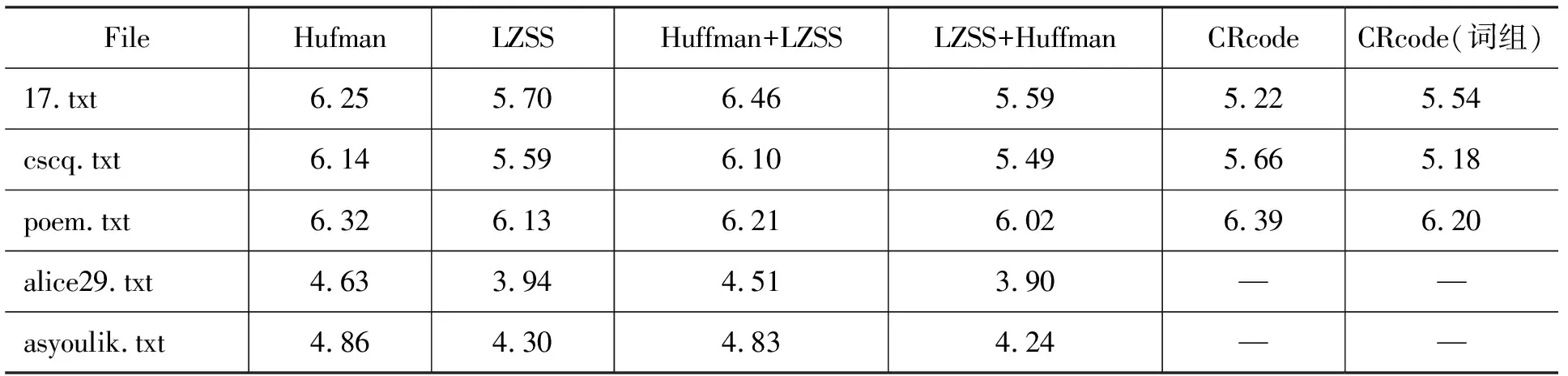
表1 打乱语义的压缩算法对压缩率的影响
打乱语义压缩算法的使用,使其他压缩算法不能或错误地理解了数据流中的语义信息,从而对压缩效果造成不利影响。如Gzip压缩算法联合使用LZSS与Huffman算法[16],由于LZSS打乱了语义,再对经LZSS处理后的数据进行Huffman压缩时,就不能正确理解数据中的语义信息。同样,若对经Huffman编码的数据进行LZSS压缩,由于Huffman输出结果是变长编码的组合,而LZSS字符串的比较是以字节为基本单位,以字节为单位对不等长编码的数据进行操作,完全割裂了数据流中的语义特征,从而严重损坏了压缩率。
表1为HitIct Corpus[17]与Canterbury Corpus中5个文本文件使用Huffman与LZSS的压缩结果,其中Huffman与LZSS采用文献[18]中的代码,CRecode为本文提出的压缩算法,CRecode(词组)包含对频率最高的768个双字词组的编码,单位为bpc。
Huffman与LZSS是两种不同的压缩算法,前者是根据字符的概率分布不平衡原理,而后者是用指针代替数据流中的重复字节串,两者的作用本质上是互补的,但这有个前提,是两种算法要能正确对对方的压缩数据进行理解,能正确地区分出语义字符,但是在表1中,由于Huffman与LZSS都为打乱语义的压缩算法,其压缩结果如果再采用另一压缩算法对其压缩,其压缩性能几乎没有增加,有些反而不增反减,如对样本17.txt,单独采用Huffman可压缩掉22%的存储空间,单独采用LZSS可压缩掉29%,如果先用Huffman算法,再用基于变长前缀码的LZSS算法进行压缩,可以减少存储空间44%(0.22+(1-0.22)×0.29=44%),即4.48bpc,而表1中两者结合最大才5.59 bpc,相差25%,可见语义维持对压缩性能的影响是巨大的。
对于中文压缩算法的而言,目前普遍的作法是将英文压缩软件直接应用到中文数据上,但是由于中英文编码方式的不同,英文使用的是单字节的ASCII编码,采用基于单字节的压缩算法,本质是符合英文数据流的语义要求的,若将其直接用于中文数据流上,由于中文采用多字节编码,算法从物理上割裂了编码中蕴含的语义信息,从而可能降低压缩率。
第二种作法是扩大压缩算法运算的基本单位,如将字符比较及字符概率计算的基本单位扩大到多字节方式,这种方式对于基于统计的压缩算法来讲,能较大的提高算法的压缩率,但对于基于字典的压缩算法来讲,反而降低了压缩率。
第三种方法是考虑中文大字符集的特点,对汉字进行重新编码,形成基于“中文字符”的Huffman压缩算法。如Ong[19]根据被压缩文本中汉字的频率分布,为汉字分配4到20bits长的码字。Vines和Zobel实现了一个基于大规模的汉语语料库的汉语文本的压缩算法[20],该算法压缩性能很高,平均压缩比达到2.25(3.56bpc)。
我们知道,数据流中所包含的信息量由熵和算法信息内容KCC组成,其和为常量或近似于常量[21],对信息的先验知识了解越多,压缩效果就越好。因此,好的压缩算法必须能充分利用数据流中的熵和KCC信息,而KCC与语义信息密切相关,在信息熵一定的情况下,对数据流中的语义信息理解、利用的越多,取得的压缩效果也就越好。上述三种方法,第一种方法直接将中文数据单字节化,以压缩ASCII编码数据的方式压缩ANSI编码的中文数据,其结果是不能充分利用中文数据流中蕴含的字符级的语义信息(ANSI编码的中文数据以双字节表示一个汉字,字母数字等以单字节来表示,其语义大多以双字节之间的关系或单双字节之间的关系来表示)。第二种方法单纯将基于字节的压缩算法扩展为基于字符的压缩算法,在应用到基于统计的压缩算法上如Huffman编码时,虽然能提高压缩率,但由于其将Huffman编码的字符数从8 bits 256个字符扩展到16 bits 65 536个字符,对应的Huffman树的节点数目增加了256倍,从而极大地降低了压缩速度。另外,要达到最优的压缩效果,必须兼顾考虑数据流中的熵和KCC信息,联合运用多种基本压缩算法对数据进行压缩,而后两种方法,由于其压缩结果是变长的bit流,已经不具有字符意义(基于字节),其基于字节的概率分布已接近于随机数据,不再有压缩的余地。
可见,理想的中文数据流压缩算法应该至少具有两个特点:一是能维持并充分利用数据流的语义信息,二是充分兼容当前各种压缩算法/工具。
3 CRecode压缩算法
无损压缩算法的理论依据包括:字符概率分布的不平衡原理、利用数据流上下文中字符串的重复信息进行熵转移、挖掘语义信息等,这些特征,在所用源自应用的数据流中都是存在的,但对于中文数据流来讲,还表现出与英文数据流不同的特征:
1) 编码特征,中文是双字节编码,而英文是单字节编码,因此压缩算法为保持数据流中的语义信息,必须能处理双字节编码。
2) 构成英文的基本单位为字母,只有26个,而构成中文的基本单位为字,仅GB2312中的汉字就达6 763个,因此,每种语言基本单位中所含的信息量是不同的。
3) 中文字词概率分布的不平衡有着与其他语言不同的特点[22]。表2为本文统计的部分ANSI编码格式的中文文本文件中字符的分布情况,可以看出,前128(该数字由CRecode的编码方式决定)个字符的字频达到50%以上,前240个达60%以上,前2 288个97%以上。
4) Huffman编码的固有缺陷:Huffman编码在字符的分布概率等于1/2的整数幂时压缩效果最好,如果字符的分布概率与1/2的整数幂相差较大时性能会很差[24]。另外,Huffman编码为变长编码,其输出结果不易被其他压缩算法再处理。

表2 中文文本中字符的分布情况
为充分考虑中文数据流的特点,克服连续变长编码如Huffman编码的固有缺陷,增强统计编码与其他压缩算法的结合性,本文提出了CRecode压缩算法。该算法采用非连续变长编码方式,即根据数据流中的字符频率分布,分别分配8、16最多24位长的编码,最大限度保持其语义特征。
3.1 CRecode压缩数据格式
CRecode数据格式见图4。

图4 CRecode压缩数据格式
FFFF:16 bit CRecode压缩文件标识,供解码器判断是否为CRecode压缩文件。
Stream Flag:8 bit流标识,用于区别数据流压缩方式,0x00为ANSI编码中文数据流静态压缩方式,0x01为ANSI编码中文数据流动态压缩方式。
Char LEN:16 bit字符字典长度,即字符个数;若Stream Flag为0x00静态压缩方式,则该域为8 bit,域值为静态编码字典指针。
Phrase LEN:16 bit短语/词组字典长度,若为0x0000则无短语/词组字典。中文数据流基本上是由词组组成,以词组为单位进行压缩则能获得更大的压缩率。
Character Dictionary:字符码表,以在数据流中出现的频率由大到小排列,每个码字16 bit。
Phrase Dictionary:若Phrase LEN域不为0x0000,则表示支持词组编码。该域的第一字节为词组长度标识,用于标识双字词与多字词。若为0x00则为双字词,若为0x01则含有多字词,在这种情况下,该标志后2 byte指未双字词长度,然后为32 bit双字词组,以频率排序,以此类推。
Data:为压缩数据。
EOF:16 bit数据结束标记。
MD5:128 bit MD5校验值,校验压缩数据完整性。
3.2 CRecode对ANSI编码中文数据流的压缩算法
CRecode有静态及动态两种压缩方式,根据用户对压缩速度及压缩率的要求,可以指定压缩方式。静态压缩方式使用CRecode自带的根据汉语频率字典中统计的字、词使用频率建立的编码字典,速度快,不需要传输码表。动态编码根据数据流动态统计字、词频率,需要对压缩数据进行二遍扫描,速度慢,但压缩效果好。动态方式由于要传输码表,在文件较小的情况有可能压缩率不及静态方式,这时可能由用户指定压缩方式,或由CRecode对两种方式下的压缩率进行比较,自动选择最佳方式。
CRecode对字符及词组进行编码时,先对压缩数据进行扫描,统计出字符及词组的使用频率,按使用频率自大到小分别排序,然后根据每个字符/词组在排序表中的索引进行编码。输出时,先输出CRecode压缩文件标识FFFF,然后依次输出前面定义的相关标识字段、字编码表长度、词组编码表长度,再依次输出排序表中的字符及词组(只输出字符/词组原编码),最后是压缩数据、压缩文件结束标志EOF、MD5校验值。编码格式见表3、表4。
3.3 解压缩算法
CRecode读入数据,首先根据数据流的前两字节的值判断是否为CRecode压缩数据,若不是CRecode压缩数据则不做任何操作,原样输出数据,否则,根据流标识判断是哪种压缩方式,如果是静态压缩方式,则根据自带的码表解码,如果为动态压缩方式,则依次读入字、词组码表长度,字词码表,然后读入数据进行解压缩。解压缩时根据数据的第一字节的值,确定该码字的字节数,然后根据该码字求出码表的索引值,最后输出码表中该位置的编码,循环往复。

表3 字符编码表(不含词组)
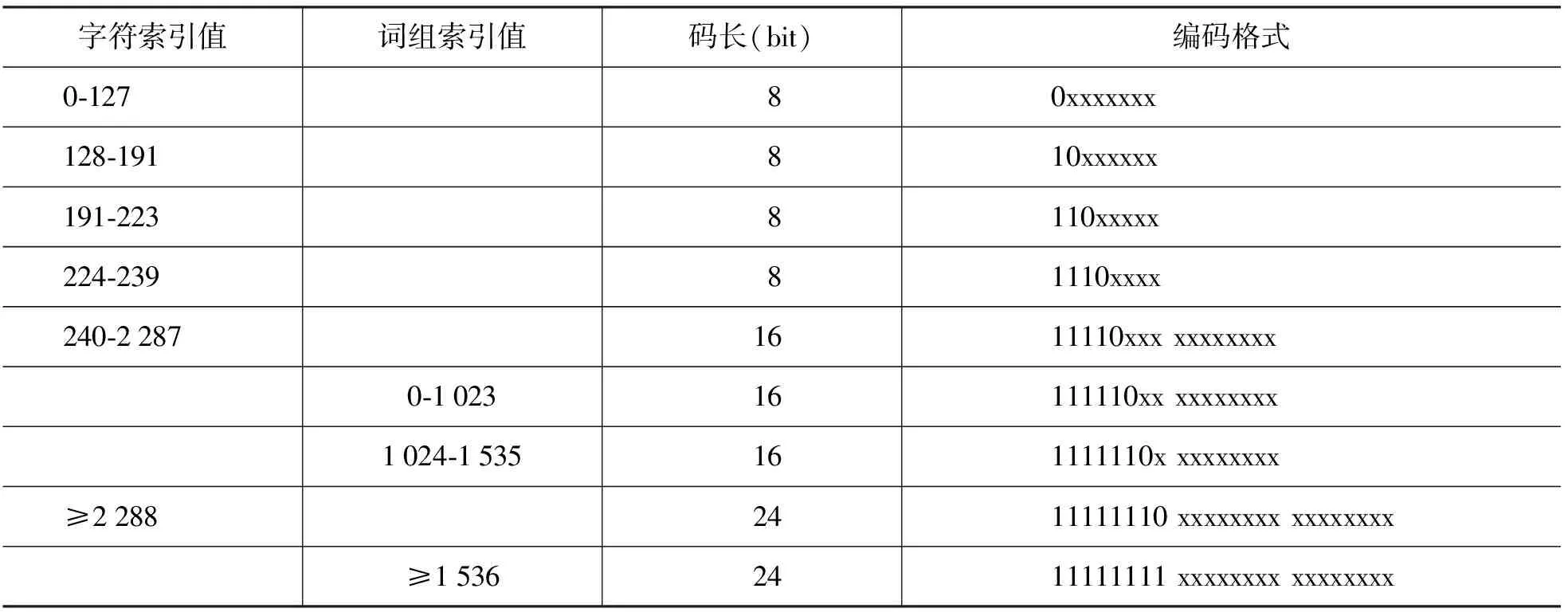
表4 字符编码表(含词组)
3.4 性能分析
对于表3所示的编码方式,CRecode根据字符的使用频率对字符重新编码,使用频率最高的240个字符采用8位编码,根据总字符数是否大于 4 336,其他字符分别采用16位或24位编码。
令测试文件中的字符总数为N(对于GB2312,N<7 445),其中单字节编码字符的数量为N0个(对于GB2312,N0< 588),fi为每个字符的使用频率,则可以求出CRecode编码的累积熵(压缩率bpc)为:
其中,S为测试文件的字节数,S=1×N0+2×(N-N0)。
进一步设使用频率索引值≤240的单字节编码字符数为N1个,为计算方便,假定其索引值为0到(N1-1),使用频率索引值在区间(240,2 288)上的单字节编码字符数为N2个,假定其索引值为240到(239+N2),则使用频率索引值大于2 287的单字节编码字符数为(N0-N1-N2)个,假定其索引值为 2 288 到N3(N3=2 287+N0-N1-N2),fi为每一个词或符号的出现频率,则CRecode编码节省的比特数为:
如果βCRecode>0,有
即使用频率最多的中文字符采用单字节编码所节省的比特总数大于单字节字符采用双字节或三字节编码、与中文字符采用三字节编码所浪费的比特数之和时,CRecode具有压缩效果,βCRecode越大,压缩率越高。
显然,CRecode对压缩率的贡献主要由频率最高的240个字符来完成,由表2看出,前240个字符的频率占总字符的70%左右,将其由16位重编码为8位,可节省35%左右的存储空间,由于前4 336个字符所占比例几乎已是100%,故采用24位编码的字符对压缩率的负面影响可以忽略不计。
CRecode在与Huffman算法结合时,由于CRecode只是根据使用频率对各个字符进行了重编码,重编码后的各字符的使用频率并没有发生改变,只是某些字符的编码由16位变成了8位或24位,字符的概率分布不平衡状态并没有改变,因此,CRecode与Huffman结合,并不会影响Huffman算法性能的发挥。
当CRecode与LZSS结合时,CRecode是一种基于统计的压缩算法,其与LZSS的作用是互补的,CRecode的输出格式为一到三字节的多字节混合编码方式,完整地保留了原数据流中蕴含的语义信息,包括字符串在上下文的重复信息等,因而,CRecode在与LZSS结合时仍能取得相当好的压缩效果。
CRecode在与PPM、BWT结合时,相当于对数据流进行了一遍预处理,CRecode的压缩结果并不影响产生数据流的应用中字符的使用频率及相对顺序,再采用PPM、BWT压缩时基本不会对PPM的概率预测机制及BWT的字符转换机制产生大的影响,因此,其对数据的压缩效果依然可以保持。
由此可见,由于CRecode能充分维持数据流中蕴含的语义信息,其在与其他基于字节的算法结合使用时,可以在保持CRecode算法本身所获得的压缩效果的前提下,不影响其他算法压缩性能的发挥,从而提高了整体压缩率。
对于CRecode的动态方式,其码表所占用储存空间=字符数×2 Bytes,平均码表空间在7KB左右。动态方式需预扫描一遍文件,统计字符频率,按频率对字符进行排序,然后再扫描文件编码输出,时间复杂度为O(nlog2n)(堆排序,n为字符个数),CRecode的静态方式只需在编码过程中检索码表,时间复杂度为O(n)。CRecode的解码算法只需要根据读入的码字检索码表,进行编码替换,速度非常快,时间复杂度为O(n)。CRecode支持部分解压缩。
4 CRecode性能测试
CRecode主要功能在于它能对中文数据流进行预处理,压缩数据流中的部分信息冗余,并能保持数据流中所蕴含的语义信息,以便使用现有各种基于单字节的压缩工具进行进一步压缩,从而获得更好的压缩率。从表1可以看出,当CRecode独立使用时,它的性能比Huffman编码要好,略差于LZSS算法。
表1还显示,当将CRecode编码的基本单位扩展到词组时,其对压缩率的影响有限,这是由于CRecode的压缩原理在于将出现频率最多的240个字符用8bit代替原编码中的16bit编码,大部分字符仍然采用16bit编码,极少数使用24bit编码,起压缩作用的只是前240个字符。如果使用词组编码,由于词组的码表要占用较大的空间,且由于词组的编码占用了有限的16bit码段,必然将一部分字符及词组的编码挤到24bit编码段,压缩率的大小取决于字符与词组个数与频率。同时由于词组的查找要占用大量的计算资源,致使编码极慢,得不偿失。
表5给出了HitIct Corpus中相关文本文件与90.txt在不同压缩算法下的压缩率,单位为bpc,测试软件为Huffman、LZSS、WinRAR 3.71 官方简体中文版、gzip v1.2.4 win32、bzip2 v1.0.4、PPMVC v1.2、WinRK v3.1.2。
Ong[19]的多级4-bit编码(OngCode)对字符按频率进行4、8、12、16及20bits的编码方式, 为了比较CRecode编码方式与OngCode在与其他压缩工具结合时的性能优劣,表5列出了选自HitIct Corpus中的3个文本文件及90.txt(该文件为18M的外国文学合集)分别由CRecode和OngCode处理后再由其他压缩软件压缩后压缩率的变化情况。
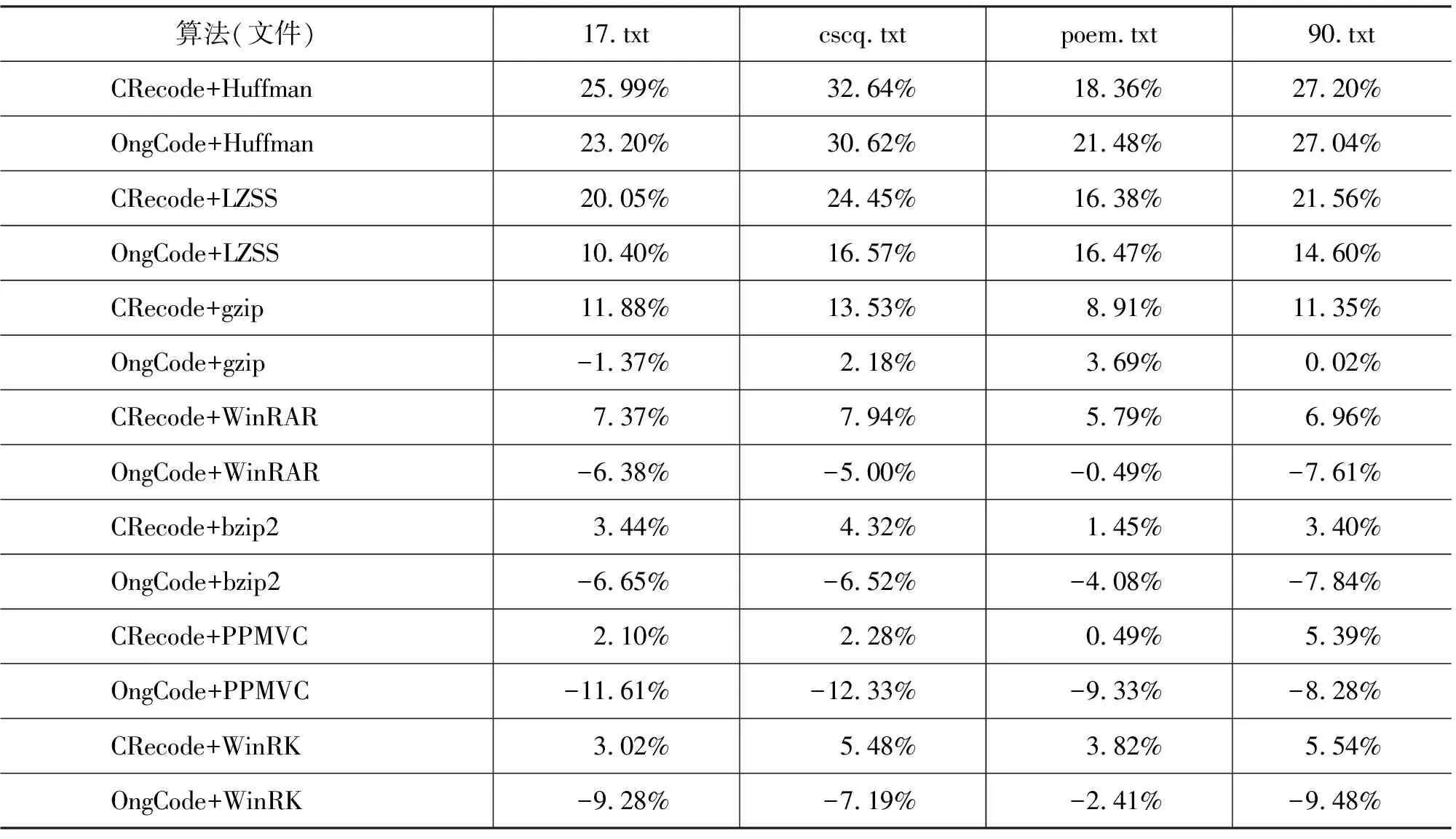
表5 不同压缩算法与CRecode和OngCode结合后的压缩率变化情况(提高百分比)
可以看出,CRecode和OngCode在与基本压缩算法Huffman和LZSS结合时都较大的提高了总体压缩率,但在与其他压缩工具结合时,CRecode的性能远高于OngCode,与OngCode结合的性能不升反降,最大降低了12.33%,这说明虽然OngCode的多级4-bit编码方式提高了码位的利用率,但是由于它的4、12、20比特码长打乱了以8bits为单位的字节边界,对蕴含在数据流中的语义造成破坏,从而降低了压缩率,其本质上是一种打乱语义的压缩方式。
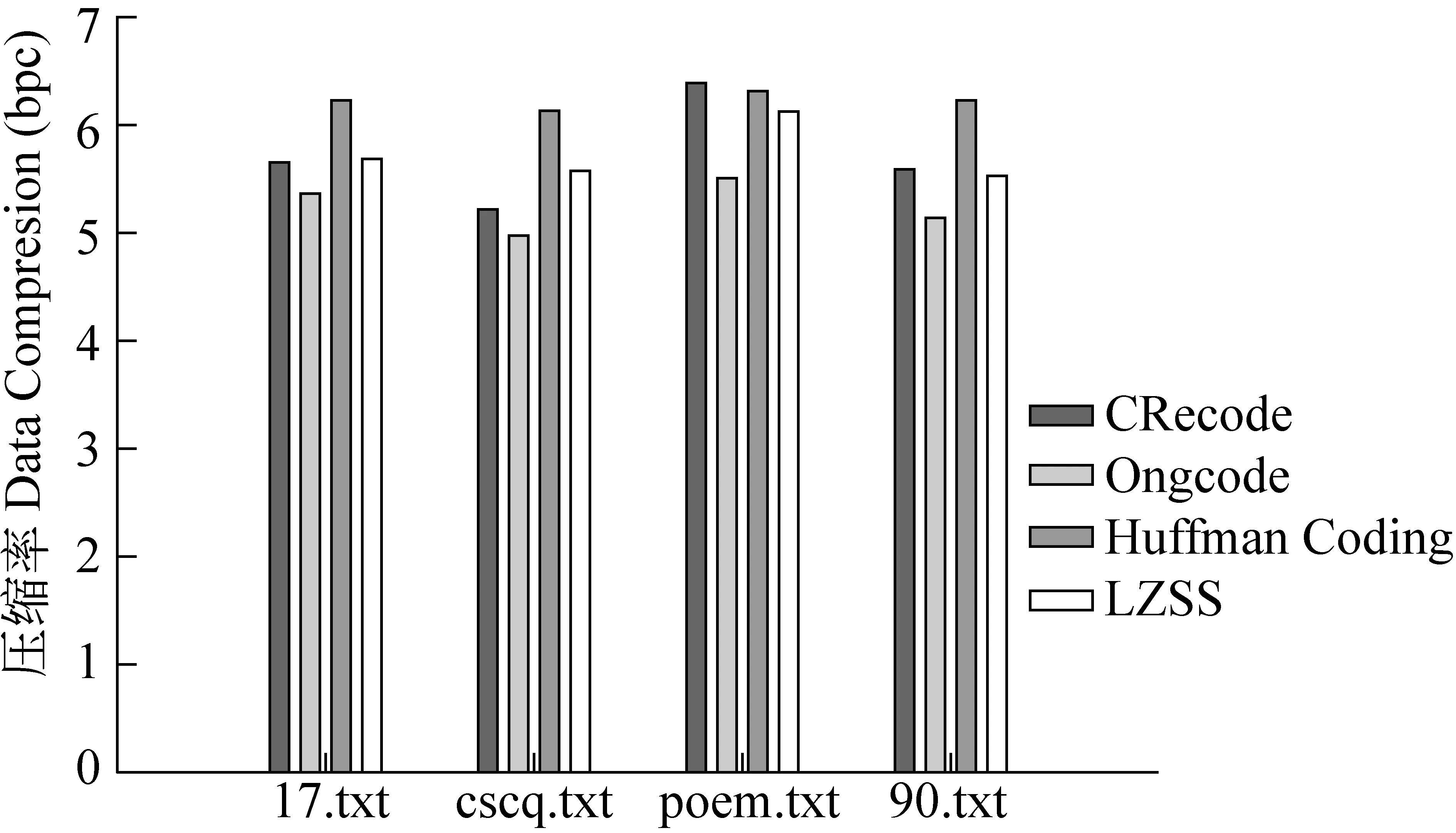
图5 CRecode、OngCode、Huffman、LZSS压缩率比较
CRecode包含8、16、24位三种码长,OngCode包含4、8、12、16、20位五种码长,两者都属于非连续变长编码,而Huffman属于连续变长编码方式,图5为三种编码方式单独使用时的压缩率示意图,可见,单独使用时,OngCode的性能最好,CRecode次之,Huffman最差。
为了进一步测试CCRecode的性能,我们用建立HitIct Corpus时所用的当代文学测试样本对CRecode编码与4个压缩工具的结合性能进行了测试,该样本集包含90个文本文件,大小分布在117KB与18M之间,总大小256M,全部来自互联网。获得的测试结果如表6所示。
由此可见,对于中文文本,经CRecode编码后Huffman编码可获得20%~30%的性能提升,LZSS、 gzip、 WinRAR、 bzip2、PPMVC可分别平均获得20%、10%、7%、4%及4%以上的性能提高,在与PPMVC算法结合时获得了最大2.26bpc、平均2.80bpc的压缩率(即压缩比最大3.54、平均 2.86),具有很高的应用价值,完全可以做为通用压缩工具的中文数据流压缩接口。
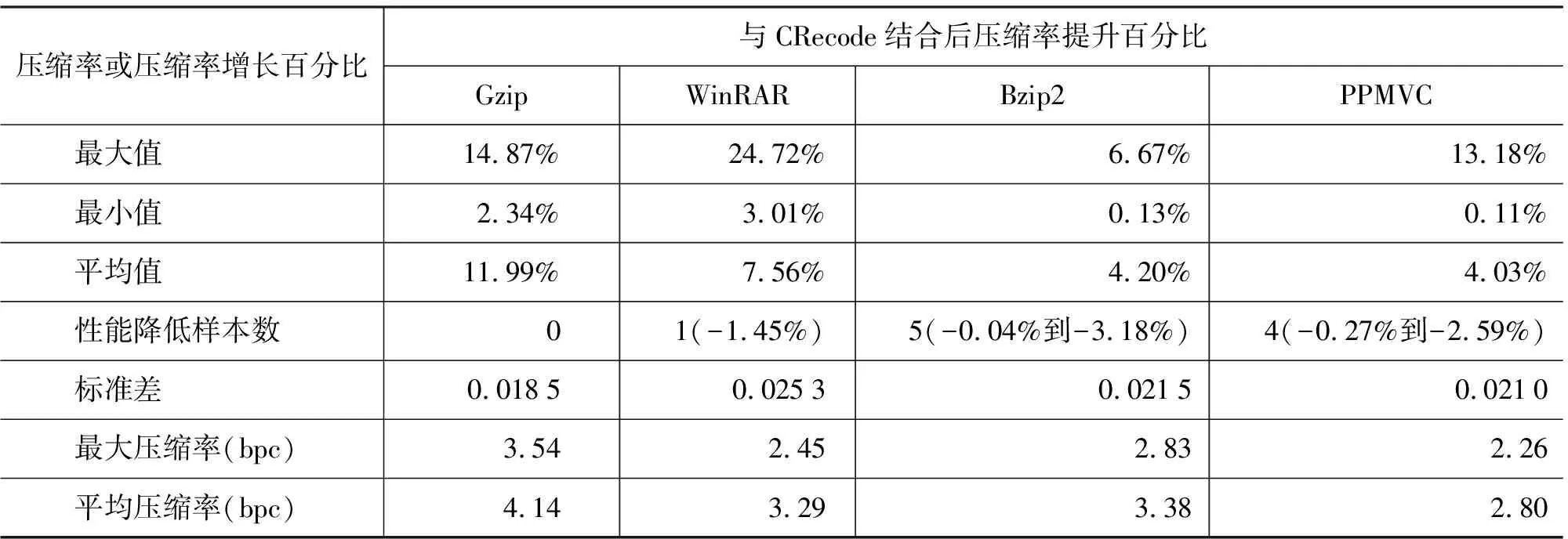
表6 CRecode在90个样本上的结合性能测试结果
5 结论
本文介绍了一个能对中文数据流进行预处理的压缩算法CRecode,它克服了Huffman算法在压缩中文数据流时打乱数据中蕴含的语义信息及在字符分布概率偏离1/2的整数幂时性能下降的缺陷,能与各种压缩算法、压缩软件配合使用,使其压缩性能提高4%~30%,平均压缩率最大可达2.80bpc,即 2.86 的压缩比。CRecode本质上是一种熵编码方式,本文的创新意义在于,采用三级8比特编码方式避免了熵编码方式对其他冗余信息的损坏(即维持了语义),在对数据流中的编码冗余进行适度压缩的前提下又保持了对其他压缩算法的兼容性,最终提高了压缩率。在实验中我们还发现,虽然WinRK是目前文本压缩领域最优秀的压缩工具[24],但其在中文文本文件的压缩性能却远逊于PPMVC,甚至于bzip2,这更说明了对编码冗余进行预消除的重要性,这也是CRecode的最大贡献,而事实上,对数据流进行预处理正是当前无损压缩领域的研究热点之一。实验表明,CRecode作为独立压缩算法,可获得优于Huffman编码、近似于LZ系列算法的性能。
[1] Huffman, D. A. A Method for the Construction of Minimum-Redundancy Codes [C]//Proc. IRE 40, 9 (Sept.), 1952: 1098-1101.
[2] Ziviani, N., Moura, E., Navarro, G., & Baeza-Yates, R. Compression: a key for next-generation text retrieval systems[J].IEEE Computer, 2000, 33(11): 37-44.
[3] Witten, I., Moffat, A., & Bell, T. Managing gigabytes 2nd [M]. Morgan Kaufmann Publishers. 1999.
[4] Ziv, J., and Lempel, A. A Universal Algorithm for Sequential Data Compression [J]. IEEE Transactions on Information Theory, 1977, 23(3): 337-343.
[5] Ziv, J., and Lempel, A. Compression of Individual Sequences via Variable-Rate Coding [J]. IEEE Transactions on Information Theory,1978,24(5):530-536.
[6] J. A. Storer and T. G. Szymanski. Data Compression via Textual Substitution [J]. Journal of the ACM, 1982, 29: 928-951.
[7] Welch, T. A. A Technique for High-Performance Data Compression [J]. Computer, 1978, 17(6): 8-19.
[8] 王忠效.汉语文本压缩研究及其应用[J].中文信息学报,1997,11(3):57-64.
[9] 华强. 中文文本压缩的LZSSCH算法[J]. 中文信息学报, 1998, 12(1): 50-56
[10] T. Bell, J. Cleary, and I. Witten. Data compression using adaptive coding and partial string matching [J]. In: IEEE Transactions on Communications, 1984, 32 (4): 396-402.
[11] A. Moffat. Implementing the PPM data compression scheme [J]. IEEE Transactions on Communications, 1990, 38 (11): 1917-1921.
[12] Joaquín Adiego and Pablo de la Fuente. On the Use of Words as Source Alphabet Symbols in PPM [C]//Data Compression Conference (DCC’06), 2006: 435.
[13] Peiliang Wu, W. J. Teahan. Modelling Chinese For Text Compression [C]//Data Compression Conference (DCC’05), 2005: 488-488.
[14] M. Burrows and D. J. Wheeler. A Block-sorting Lossless Data Compression Algorithm [R]. Digital Systems Research Center Research Report 124, May 1994.
[15] Matt Mahoney. Rationale for a Large Text Compression Benchmark[EB/OL]. Online. Internet. Available from http://www.cs.fit.edu/~mmahoney/compression/rationale.html, 5, Jan. 2008.
[16] P. Deutsch. RFC1951: DEFLATE Compressed Data Format Specification version 1.3 [Z]. 1995.
[17] 常为领, 云晓春, 方滨兴, 王树鹏. HitIct: 中文无损压缩算法性能评估测试集[J]. 通信学报,2009,30(3):42-47.
[18] Nelson M., Gailly J. The Data Compression Book, 2nd edition[M].M&T Books,New York,NY,1995.
[19] Ghim Hwee Ong and Shell Ying Huang. Compression of Chinese Text Files Using a Multiple Four-Bit Coding Scheme [C]//IEEE Singapore ICCS/ISITA ’92, Nov. 1992:1062-1066.
[20] Phil Vines, Justin Zobel, Compression Techniques for Chinese Text [J]. Software-Practice and Experience, 1998, 28(12):1299-1314.
[21] David Salomon. Data compression: The Complete Reference, Third Edition [M]. New York : Springer, 2004: 134-155.
[22] 北京语言学院语言教学研究所.汉语词汇的统计与分析[M].北京: 外语教学与研究出版社,1985.
[23] Wikipedia, the free encyclopedia. Huffman coding[BE/OL]. Online. Internet. Available from http://en.wikipedia.org/wiki/Huffman_coding. May 2010.
[24] Maximum Compression’s English Text compression test[BE/OL].Online.Internet.Available from http://www.maximumcompression.com,3,Sept.2009.
