一类动力系统的极限环及其数目和分布*

黄赪彪

(中山大学工学院，广东 广州 510275)

动力学和控制中，不少问题可以归结为以下平面二次动力系统极限环的研究

dx/dt=α1x+α2y+α3x2+α4xy+α5y2

dy/dt=β1x+β2y+β3x2+β4xy+β5y2

(1)

其中，αi,βi(i=1,2,…,5)是实参数。系统(1)的各种解法中[1-13]，以广义谐函数为基函数的摄动增量法(PI)的优点显著[5]。其特点是独立给出增量法的初值，解答简洁、精度良好，能算出极限环的表达式、频率、周期、振幅、偏心矩、稳定性，且能给出系统极限环振幅与参数的关系式，从而可以确定极限环的数目，并利用现有结果，讨论其分布位置。本文将利用该法的这些特点，详细分析一类动力系统的相关解答。与龙格-库塔(Runge-Kutta简记R-K)数值积分法比较，计算结果吻合良好。

1 摄动增量法概述

摄动法引进控制参数ε≥0，系统(1)改写为

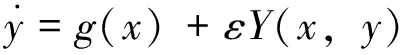
(2)

式(2)中，(·)=d( )/dt(下同)，

X(x,y)=α1x+α3x2+α4xy+α5y2

Y(x,y)=y(β2+β4x+β5y)

g(x)=β1x+β3x2

引进变量替换

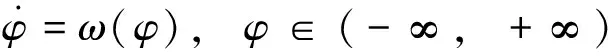
(3)

满足ω(φ+2π)=ω(φ)>0。易知变换(3)不改变系统(2)的拓扑结构。于是式(2)变为

ωx'=α2y+εX(x,y)

ωy'=g(x)+εY(x,y)

(4)

式(4)中，( )′=d( )/dφ(下同)。设系统(4)周期解的横坐标x为广义谐函数

x=acosφ+b,φ∈(-∞,+∞)

(5)

式(5)中，a、b分别是x坐标的振幅和偏心距。将式(5)代入式(4)，得

y=-(aωsinφ+εX)/α2

(6)

将式(6)代入式(4)第二式，有

ω(aωsinφ)′=-εωX′-α2g(x)-α2εY

(7)

式(7)两边同乘以asinφ并对φ积分，得

ω={2α2[v(acosφ+b)-v(a+b)]+

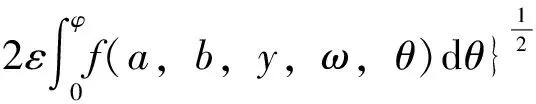
(8)

这里，

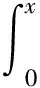
f(a,b,y,ω,θ)=a(ωX′+α2Y)sinθ

为了确保式(8)给定的ω的连续性，式(4)中的g(x),X(x,y),Y(x,y)须满足一定的条件。

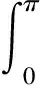
(9)

(10)

改写式(6)为

α2y+aωsinφ+εX=0

(11)

经变换(3)，系统(1)周期解的相关量a,b,y,ω可由式(8)-(11)确定，但难以精确求解。下面以摄动增量法近似求解之。

取ε≈0，由式(5)及(8)-(11)得

x0=a0cosφ+b0

(12)

y0=-a0ω0sinφ/α2

(13)

ω0={2α2[v(a0cosφ+b0)-

(14)

v(-a0+b0)-v(a0+b0)=0

(15)

(16)

联立式(12)-(16)，可得a0,b0。于是，增量法的初值为a0,b0,y0,ω0。

给参数ε予小增量Δεi,i=1,2,…,相应地，系统的初值的增量分别为Δa,Δb,Δy,Δω。令

εi=εi-1+Δεi,ai=ai-1+Δa,bi=bi-1+Δb

yi=yi-1+Δy,ωi=ωi-1+Δω,i=1,2,…

(17)

相应地，

xi=aicosφ+bi

(18)

yi=-(aiωisinφ+εiXi)/α2

(19)

(20)

式(19)中，Xi=X(xi,yi)。式(20)表示的ωi难以精确求解。为近似求解方便起见，分别展开

yi,ωi,Δy,Δω为富氏展式：

(21)

(22)

(23)

(24)

将式(17)及(18)代入式(11)并略去关于Δa,Δb,Δy,Δω的二次以上的高次项，得

-α2yi-aiωisinφ-εiXi

(25)

类似于式(25)，由式(8)可得

(26)

式(26)中，

(27)

类似地，由式(9)得

(28)

由式(10)，可得

(29)

式(25)-(29)中,( )|i=( )|ε=ε1,a=ai0,b=bi,y=yi,ω=ωi。将上述各式中所含的三角函数cosφ,sinφ的幂及乘积化为倍角的三角函数及其代数和形式，并利用谐波平衡原理，可得关于

ΔC0,ΔC1,ΔC2,…,ΔCm;ΔD1,ΔD2,…,ΔDm;

ΔP0,ΔP1,ΔP3,…,ΔPm;ΔQ1,ΔQ2…,ΔQm;Δa,Δb

为独立变量的线性代数方程组

AZ=B

(30)

式(30)中，

Z= [ΔC0,…,ΔCm;ΔD1,…,ΔDm;

ΔP0,…,ΔPm;ΔQ1,…,ΔQm;Δa,Δb]T

上式中，Ai,j,Bi(i,j=1,2,…,4m+4)的计算涉及一系列三角函数及三角级数乘法,限于篇幅,不叙述。

求解方程组(30)得到Z并将之代入式(20)、(21)及(17)。重复上述步骤，设经参数ε的k次增量，满足εk=1为止。此时的ak,bk,yk,ωk即为所求的a,b,y,ω。于是，绕奇点(0，0)的周期解、频率和周期的表达式分别为

x=acosφ+b

(31)

(32)

(33)

(34)

周期解的稳定性特征指数

(35)

(36)

则稳定性指数为

(37)

当γ<0(>0)时周期解稳定(不稳定)。

周期解的数目及其随参数的变化而变化的演变过程，可由式(9)和(10)定量给出。比如系统(1)关于参数β2与周期解振幅的关系曲线为

式(38)中，

G(x,y)=β1x+β3x2+β4xy+β5y2

通过曲线(38)，可以直观了解系统的所有周期解随参数β2变化而产生、稳定、分岔与消失的全过程。而周期解与其他参数的关系，也可类似于式(38)表示。将式(36)代入式(34)，系统周期解的周期为

(39)

2 计算结果

式(1)中的各参数分别取为：

α1=0.001,α2=0.72,α3=0.28,α4=0.02

α5=0.276,β1=β3=-0.95,β4=4,β5=0.982

此时系统有两个奇点：不稳定焦点F(0,0)及鞍点S(0.542 516 586 263 355 176 387 758 713 052 45,-2.529 172 980 197 140 495 658 553 459 823 5).

周期解关于参数β2的分岔曲线由式(38)确定，无量纲化(下同)图形见图1。周期解的振幅a随参数β2的变化而产生、稳定、分岔和消失的演变过程说明如下：

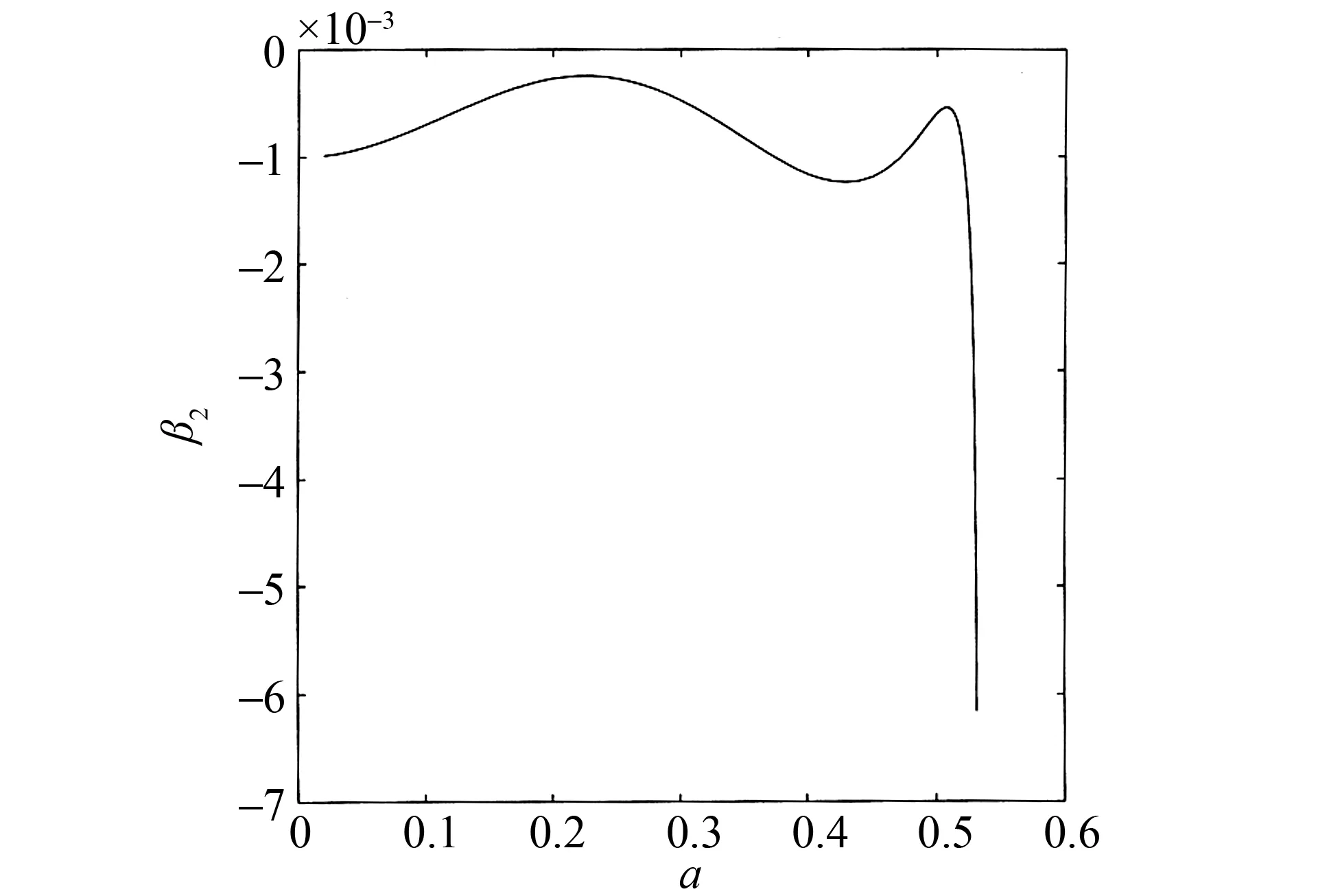
图1 参数β2与振幅ai的关系曲线(无量纲化下同)

1)β2∈(-∞,-0.006 160 949)时，没有周期解；

2)β2∈[-0.006 160 949,-0.001 237 986 2)时，γ>0，有一个不稳定周期解；

3)β2=-0.001 237 986 2时有两个周期解，振幅a=0.43和0.5226，小者半稳定(左不稳定，右稳定)，大者不稳定；

4)β2∈(-0.001 237 986 2,-0.000 986 182 9)时，有三个周期解，依振幅由小至大(下同)分别为不稳定，稳定和不稳定；

5)β2∈[0.000 986 182 9,-0.000 544 970 679)时有四个周期解，依次为稳定、不稳定、稳定和不稳定；

6)β2=-0.000 544 970 679时有三个周期解，依次为稳定、不稳定、半稳定；

7)β2∈(-0.000 544 970 679,-0.000 247 052 445 03)时有两个周期解，依次为稳定和不稳定；

8)β2=-0.000 247 052 445 03时有一个半稳定周期解(左稳定右不稳定)；

9)β2>-0.000 247 052 445 03时周期解消失。

取β2=-0.000 75∈[-0.000 986 182 9,-0.000 544 970 679)，由5)知系统绕焦点(0,0)有四个环Li(i=1,2,3,4)，较小的三个是极限环(振幅ai、偏心距bi、周期Ti、稳定性特征指标γi、yi和ωi(i=1,2,3)的富氏系数见表1，较大者是过鞍点同宿环(见图2)。

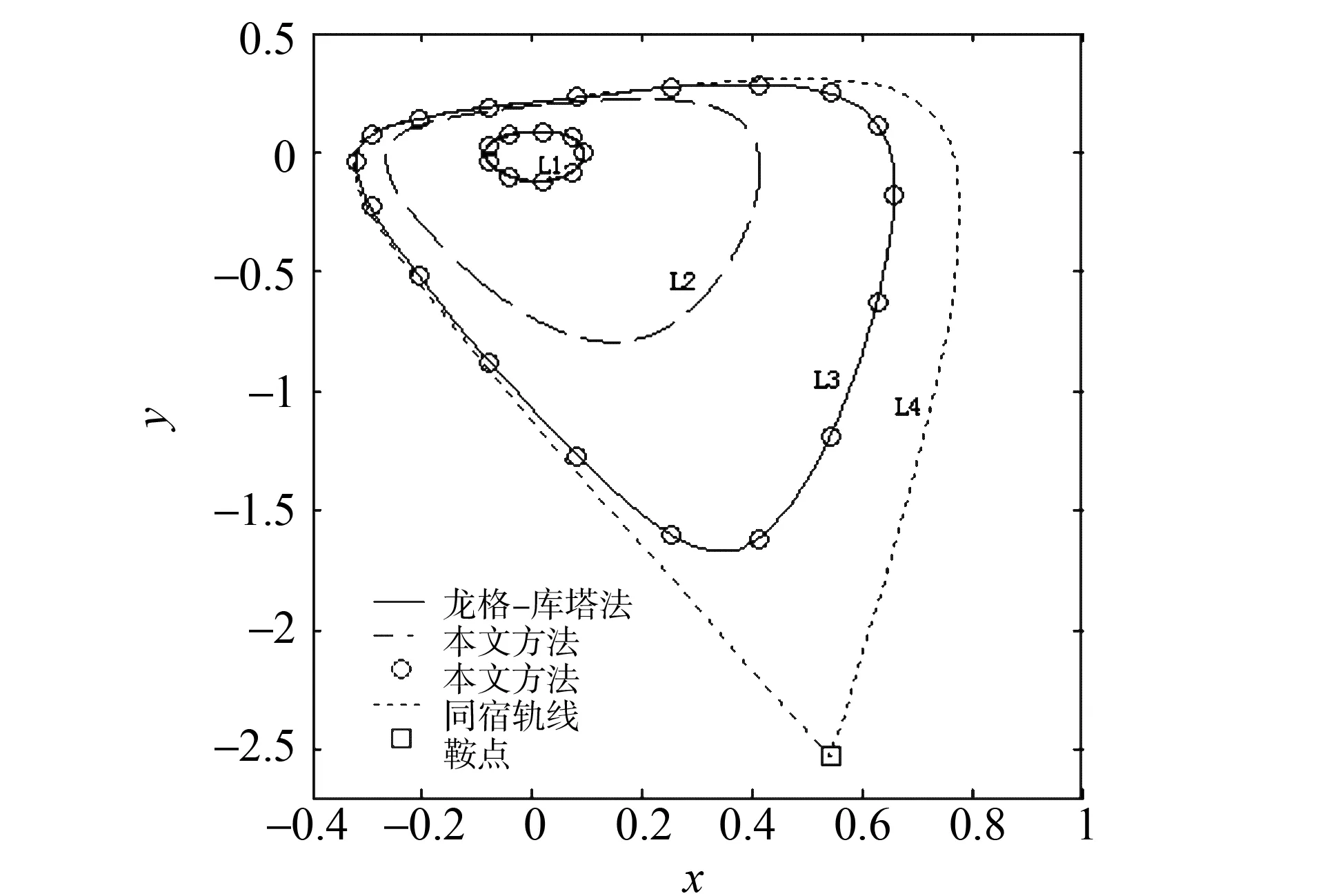
图2 极限环和同宿环的相轨线

进一步的数值搜索显示，在相平面的有限域D内，存在一条无切曲线L6和两条渐近曲线L4及L-LL(见图3)[14]，将区域D分割为四子域D1、D2、D3、D4。其中，无切曲线L6由一根曲线段连接两根直线近似构成，曲线段在原点附近过点(-5,-35.028 334 350 141 722 808 302 802 15),(0.182 1,-2.8), (-0.029 75,-1.2), (-0.332 057,-0.16),(-0.34,.001 5), (-0.2,0.152 5),(0.,0.216 5),(0.5,0.342 065 050 151 5),(1,0.463 730 501 515),(15,3.843 888)，两直线的方程近似为：

y=5.951 867 983 861 62x-5.758 160 080 691 9

x∈(-M1,-5],

y=0.241 505 101 379 31x+0.221 312 479 310 34

x∈[15,M2).

上式中，M1,M2>0是任意大的实数(下同)。渐近曲线L4由一根曲线段连接两根直线近似构成，曲线段在原点附近过点(-1,-0.016 2),(-0.7,0.056 9),(-0.4,0.130 8),(-0.2,0.181 58),(0,0.236 32),(0.2,0.305),(0.4,0.418 4),(0.7,0.815 9),(1,1.600 5), (1.5,3.565 2), 两直线的方程近似为：

y=0.241 505 101 379 31x+0.217 312 479 310 34

x∈(-M1,-1]

y=5.951 867 983 861 62x-5.758 160 080 691 9

x∈[1.5,M2)

另一条渐近曲线近似由鞍点出发的两条射线组成，两条射线的方程分别为(见图3)：

图3 无切曲线及渐近线

L:y=5.951 867 983 861 62x-5.758 160 080 691 9

x∈(-M1,0.542 516 586 263 355 176 387 758 713]

LL:y=-2.487 958 636 674 045x-1.178 437 624 009

x∈[0.542 516 586 263 355 176 387 758 713,M2)

由子域D1和D2上的点出发的相轨线趋向L4；由子域D4上的点出发的相轨线趋向于L-LL；子域D3内存在绕原点(0,0)(焦点)的四个环(如上述)。在极限环吸引域(记为D5⊂D3)内的点出发的相轨线趋近极限环，余者趋于L-LL。例如由点(-1e+150, 1e+150)∈D1，(-1e+150, -1e+150)∈D2出发的相轨线迅速趋近于L4，而由点(-5, -35.42)∈D5，(-5, -35.18)∈D3, (-5,-34.5)∈D2, (-5,-35.56)∈D4, (-2,2)∈D1出发的相轨线分

别L1→L10,L2→LL,L5→L4,L7→L-LL，L11→L4(见图4)。

图4 原点附近的相轨线

表1 三个极限环的a,b,γ,T,C,D,P,Q值

Table 1 Values ofa,b,γ,T,C,D,P,Qfor the limit cycles

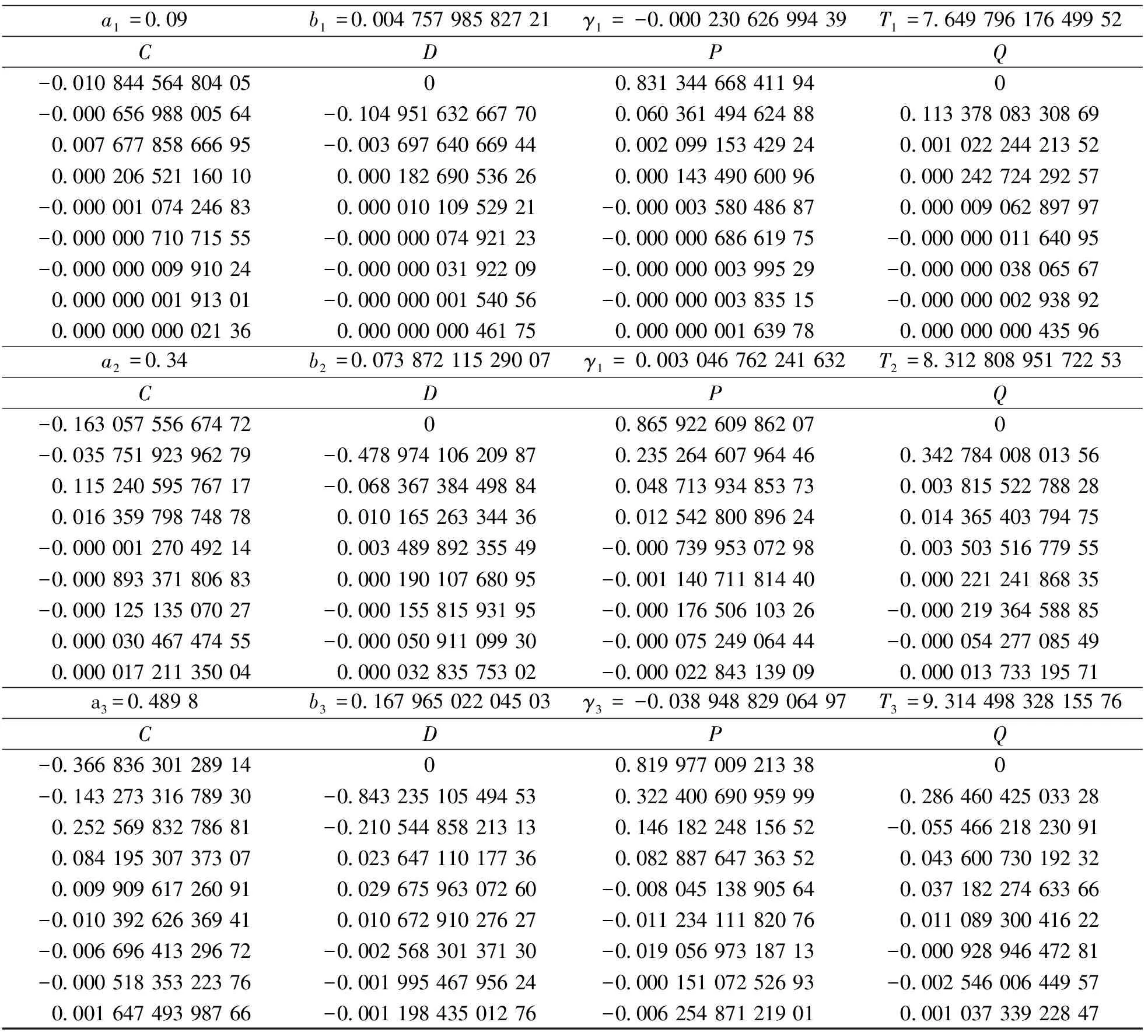
a1=0.09b1=0.004 757 985 827 21γ1= -0.000 230 626 994 39T1=7.649 796 176 499 52CD PQ-0.010 844 564 804 0500.831 344 668 411 940-0.000 656 988 005 64-0.104 951 632 667 700.060 361 494 624 880.113 378 083 308 690.007 677 858 666 95-0.003 697 640 669 440.002 099 153 429 240.001 022 244 213 520.000 206 521 160 100.000 182 690 536 260.000 143 490 600 960.000 242 724 292 57-0.000 001 074 246 830.000 010 109 529 21-0.000 003 580 486 870.000 009 062 897 97-0.000 000 710 715 55-0.000 000 074 921 23-0.000 000 686 619 75-0.000 000 011 640 95-0.000 000 009 910 24-0.000 000 031 922 09-0.000 000 003 995 29-0.000 000 038 065 670.000 000 001 913 01-0.000 000 001 540 56-0.000 000 003 835 15-0.000 000 002 938 920.000 000 000 021 360.000 000 000 461 750.000 000 001 639 780.000 000 000 435 96a2=0.34b2=0.073 872 115 290 07γ1= 0.003 046 762 241 632T2=8.312 808 951 722 53CD PQ-0.163 057 556 674 7200.865 922 609 862 070-0.035 751 923 962 79-0.478 974 106 209 870.235 264 607 964 460.342 784 008 013 560.115 240 595 767 17-0.068 367 384 498 840.048 713 934 853 730.003 815 522 788 280.016 359 798 748 780.010 165 263 344 360.012 542 800 896 240.014 365 403 794 75-0.000 001 270 492 140.003 489 892 355 49-0.000 739 953 072 980.003 503 516 779 55-0.000 893 371 806 830.000 190 107 680 95-0.001 140 711 814 400.000 221 241 868 35-0.000 125 135 070 27-0.000 155 815 931 95-0.000 176 506 103 26-0.000 219 364 588 850.000 030 467 474 55-0.000 050 911 099 30-0.000 075 249 064 44-0.000 054 277 085 490.000 017 211 350 040.000 032 835 753 02-0.000 022 843 139 090.000 013 733 195 71a3=0.489 8b3=0.167 965 022 045 03γ3= -0.038 948 829 064 97T3=9.314 498 328 155 76CD PQ-0.366 836 301 289 1400.819 977 009 213 380-0.143 273 316 789 30-0.843 235 105 494 530.322 400 690 959 990.286 460 425 033 280.252 569 832 786 81-0.210 544 858 213 130.146 182 248 156 52-0.055 466 218 230 910.084 195 307 373 070.023 647 110 177 360.082 887 647 363 520.043 600 730 192 320.009 909 617 260 910.029 675 963 072 60-0.008 045 138 905 640.037 182 274 633 66-0.010 392 626 369 410.010 672 910 276 27-0.011 234 111 820 760.011 089 300 416 22-0.006 696 413 296 72-0.002 568 301 371 30-0.019 056 973 187 13-0.000 928 946 472 81-0.000 518 353 223 76-0.001 995 467 956 24-0.000 151 072 526 93-0.002 546 006 449 570.001 647 493 987 66-0.001 198 435 012 76-0.006 254 871 219 010.001 037 339 228 47

3 讨 论

经上述分析及数值结果显示：

1) 动力系统(1)的极限环的存在性、数目及稳定性可以具体定量算出；

2) 极限环相轨、频率、周期及稳定指数的定量表达式由式(31)-(35)表示；

3) 变量替换(3)实际上是将时程空间(x(t),y(t))上系统(1)的讨论，转换成以φ为相角的相空间(x(φ),y(φ))中系统(4)的讨论。经此变换，系统极限环的振幅、偏心矩、相轨线形状及分布不变(三个极限环的相图与数值法的比较见图2),但周期改变：变换后的周期恒为2π，而时程空间中，由式(34)算得的三个极限环的周期T分别约为7.65、8.313、9.31(见表1，与数值积分的结果7.65，8.313，9.2几乎完全一致)，比如最大周期环的x-t,x-φ及y-t,y-φ曲线分别见图5、图6。

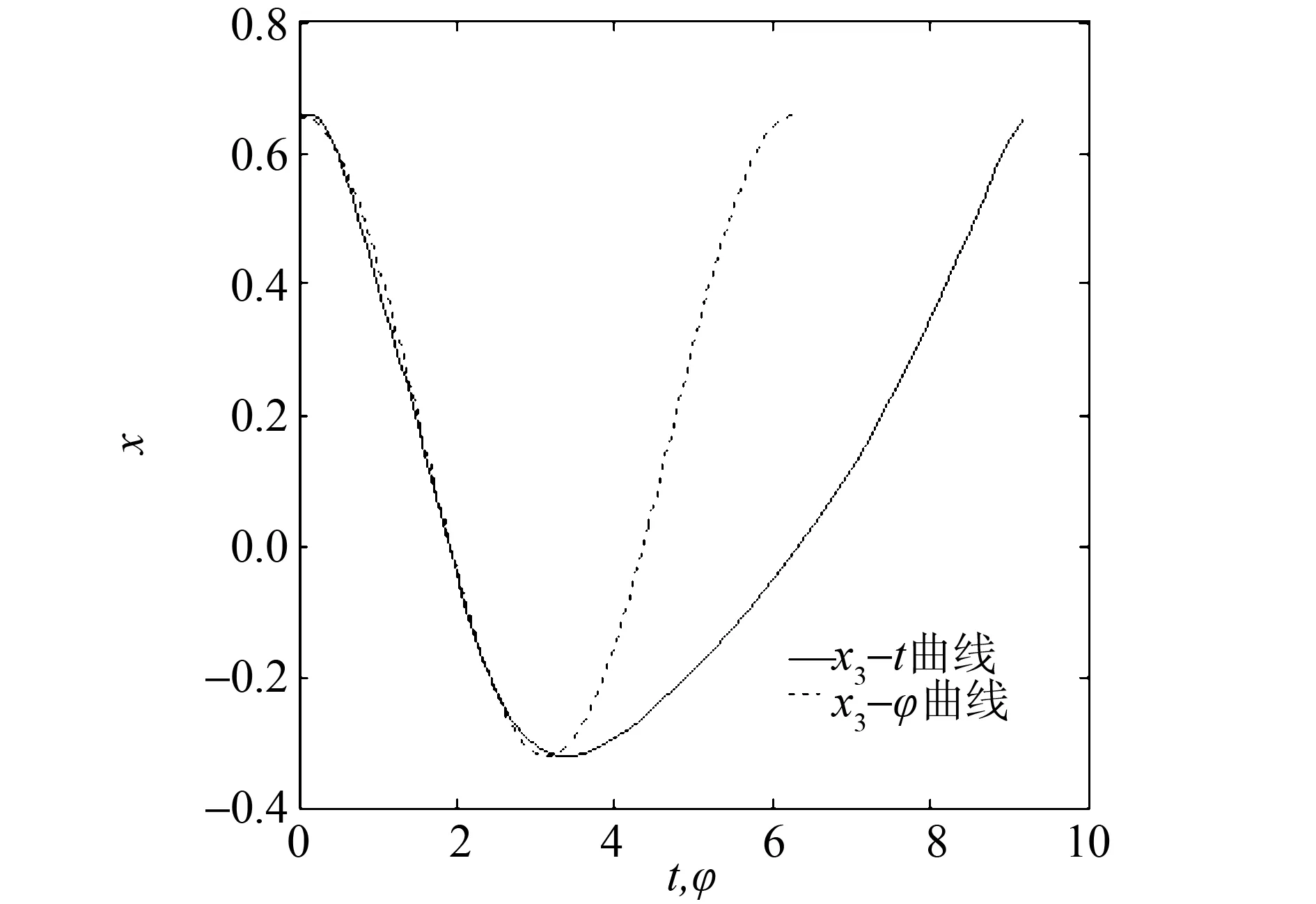
图5 x的时程和相程曲线

图6 y的时程和相程曲线

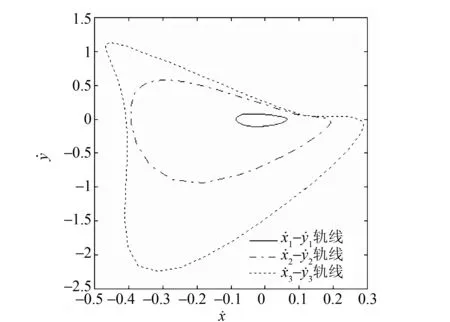
图7 三个极限环在平面上速率线

5)式(38)给定的β2-a曲线(如图1)显示，系统有四个环，一度疑为存在极限环的H(4，0)分布(目前只知道有H(3，1)分布)。经数值和解析相结合的反复分析，澄清了较大的环是同宿环的近似而不是极限环。

参考文献：

[1] NAYFEH A H, BALACHANDRAN B.Applied nonlinear dynamics[M].New York：Wiley,Analytical Computational and Experimental Methods,1995.

[2] NAYFEH A H.Introduction to perturbation techniques [M].New York：Wiley, 1993.

[3] STORTI D W, Rand R H.Dynamics of two strongly coupled van der Pol oscillators[J]. International Journal of Non-Linear Mechanics,1982,17:143-152.

[4] SPRYSL H.Internal resonance of non-linear autonomous vibrating systems with two degrees of freedom [J]. Journal of Sound and Vibration, 1987,112:63-67.

[5] XU Z, CHAN H S Y,CHUNG K W.Separatrices and limit cycles of strongly nonlinear oscillators by the perturbation-incremental method[J]. Nonlinear Dynamics, 1996,11:213-233.

[6] CHAN H S Y, CHUNG K W,XU Z.A perturbation-incremental method for strongly non-linear oscillator[J]. International Journal of Non-linear Mechanics,1996,31:59-72.

[7] CHAN H S Y,CHUNG K W,XU Z.Stability and bifurcatuin of limit cycles by the perturbation-incremental method[J]. Journal of Sound and Vibration,1997,206:589-604.

[8] CHAN H S Y, CHUNG K W,XU Z.Calculation of limit cycles, in Proceedings of the 3rdInternational Conference on Nonlinear Mechanics[C]∥ Shanghai:Shanghai University Press, 1998:597-601.

[9] CHEN G,LI C,LIU C,et al.The cyclicity of period annuli of some classes of reversible quadratic systems, DISC[J].Cont in Dyn Sys, 2006(16):157-177.

[10] GASULL A,GUILLAMON A. Viladelprat[J]. J the Period Function for Second-order Quadratic ODEs is Monotone, Qual Th Dyn Sys,2004(4):329-352.

[11] BONORINO L,BRIETZK E, LUKASZCYK J P.Properties of the period function for some hamiltonian systems and homogeneous solutions of a semilinear elliptic equation[J]. J Diff Eqns，2005(214):156-175.

[12] HUANG Chengebiao,LIU J.The limit cycles and homoclinic orbits and their Bifurcation of the Bogdanov-Takens system [J].Applied Mathematics and Mechanics.2008:29(9): 1195-1202.

[13] 黄赪彪，邬华东.平面二次系统极限环及其稳定与分岔的计算[J].中山大学学报:自然科学版，2008，47(2)：28-31.

[14] 秦元勋，索光俭，杜星福.关于平面二次系统的极限环(Ⅱ)[J].中国科学:A辑，1983(4)：417-425.