基于载荷二维分布的可靠性分析方法

高 鹏 谢里阳

东北大学,沈阳,110004

0 引言

机械零件及系统的载荷一般可以用复杂的时间-载荷历程来描述,也即可以用随机过程来对载荷历程进行数学描述。因此,当零件承受载荷多次作用时,则不能简单地应用载荷-强度干涉模型进行计算,而应该从载荷历程的统计特性出发,考虑载荷作用次数对于零件及系统可靠度的影响。近年来,有学者对载荷多次作用下零件的可靠度计算进行了研究[1-5]。文献[4]假设强度不退化,分析了载荷作用次数对可靠度的影响。文献[5]通过递推公式得到多级载荷下考虑强度退化的可靠度计算。但是,这些模型中没有考虑载荷的随机性,并且没有对载荷的随机历程进行详细阐述,导致模型中随机变量物理意义不明确,无法全面表达随机载荷多次作用时的可靠度变化规律。

本文首先对载荷历程进行了分析,提出随机载荷的二维分布：横向分布和纵向分布;然后,根据组成系统的零件间的结构关系,提出考虑共因失效时机械系统的可靠度计算公式。

1 基于载荷纵向分布的零件可靠性分析

载荷-强度干涉模型是机械零件静态可靠度分析的基础。用f s(s)、f r(r)分别表示载荷和强度的概率密度函数,Fr(◦)表示强度的分布函数,则载荷小于强度的概率也即可靠度为

这就是Freudenthal于1947年提出的著名的载荷-强度干涉模型[6]。其中,载荷和强度是广义的,载荷可以是应力、温度、腐蚀、载荷的作用次数等,强度可以是疲劳强度、抗热性、抗腐蚀性、零件的失效循环数等。该模型适用于随机载荷作用一次或者考虑个体差异的恒幅载荷作用下的可靠度计算。实际上,零件往往承受随机载荷的多次作用,这时,载荷需要用一个随机过程来描述。工程上,经常通过多次记录载荷的整个时间历程来获得多个样本,并通过对样本的统计分析得到载荷的统计特性。

对于确定时刻(或者确定载荷作用次数)通过统计得到的载荷概率密度函数,称为载荷的纵向概率密度函数,而不同时刻的纵向概率密度函数一般是不同的。用f si(si)、F ri(r i)分别表示第i次作用时载荷概率密度函数和强度的分布函数,Ri表示载荷作用第i次时零件不发生失效的概率,假设零件的初始可靠度为R0,则随机载荷作用n次(n≥1)后的可靠度为

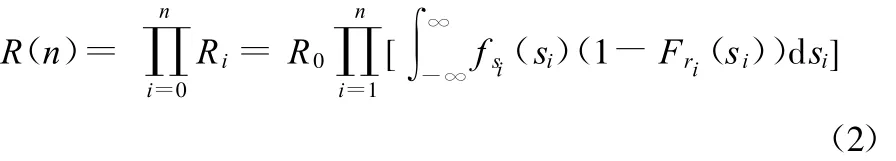
这就是基于载荷纵向分布的零件可靠度模型。

2 强度不退化时基于载荷横向分布的零件可靠性分析

对于载荷整个时间轴的统计分析得到的概率密度函数称为载荷的横向概率密度函数。通常使用的各种计数法(如雨流计数法等)得到的分布是这种分布。值得注意的是,每个样本得到的概率密度函数一般都不相同,通常使用的概率密度函数可以看作是载荷横向分布的一次实现(只统计一个样本),或者载荷横向分布的平均分布。为了对此进行描述,用Xj表示载荷横向分布某一具体实现的统计特征参数(例如对于正态分布,其统计特征参数为均值和方差;对于三参数威布尔分布,其特征参数为位置参数、形状参数、尺度参数),定义F(X)为载荷特征分布函数,f X(Xj)d X表示载荷横向分布为某一特定分布的概率,并且该分布的统计特征参数为Xj,fX(Xj)为载荷特征概率密度函数。

对于某一确定样本统计得到的横向分布,假设该确定分布的概率密度函数为 f sj(s)(注意：该概率密度函数不是特征概率密度函数),特征参数为Xj,载荷作用次数为n,则某一确定载荷si出现的次数为ni=nf sj(si)d s。令强度的概率密度函数为 f r(r),则si作用ni次后零件的可靠度为

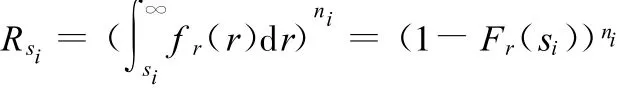
那么,随机载荷作用n次后的可靠度为

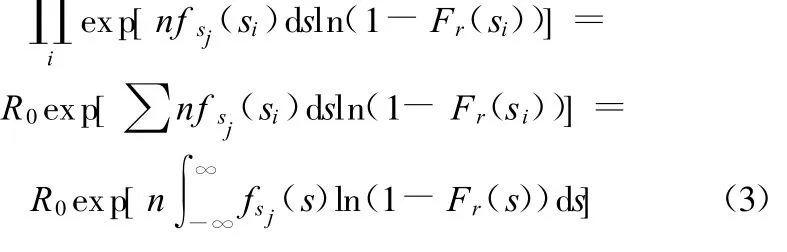
由式(3)可知,载荷每次作用的平均可靠度为

考虑到载荷横向分布的不确定性,得到随机载荷作用n次后零件的可靠度为

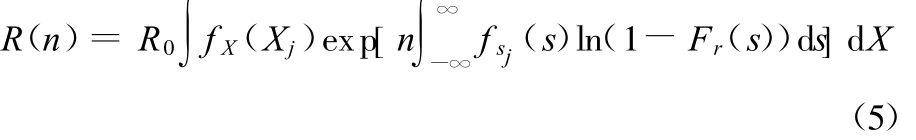
式(5)为基于载荷横向分布的零件可靠度计算公式。

为了便于工程应用,对于已经得到的多个样本,可以利用式(5)的离散化形式进行可靠性评估,也即先通过计数拟合出每个样本的概率密度函数,再按照下式进行计算：

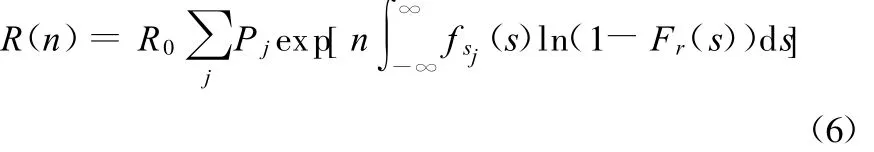
式中,Pj为经过拟合后载荷概率密度函数为fsj(s)的概率,并且可以近似地认为该概率等于概率密度函数为fsj(s)的样本个数占全体样本的比例。

这样就得到了基于载荷横向分布的、适合实际应用的零件可靠度计算公式。

3 考虑强度退化时基于载荷横向分布的零件可靠性分析

以上分析中假设了强度不退化,当考虑强度退化时,可以采用以下的近似计算方法：

对于某一确定的横向概率密度函数 f sj(s),当载荷作用n次时,大小为si的载荷的出现次数为ni=nf sj(si)d s次,其造成的损伤为nf sj(si)d s/Nsi,Nsi为si作用下的零件使用寿命。由线性损伤等效原理(这里只是为了叙述方便,实际上可以采用其他非线性等效原理),si作用ni次,相当于大小为sj0的载荷作用ni0次,并且

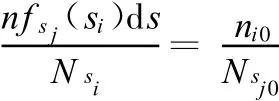
式中,Nsj0为sj0作用下的零件使用寿命。

又由零件的S-N曲线,近似得到Nsm=C,其中m、C近似为常数,得到

因此随机载荷作用n次相当于载荷sj0作用nsj0次 ,并且

于是,可以认为强度符合确定载荷sj0作用下的变化规律,而且sj0作用第q-1次时的剩余强度分布函数为Frq-1|sj0(r)。于是得到

同样,式(8)的离散化形式为

4 横向概率密度函数与纵向概率密度函数的关系

以上分析了基于载荷横向分布和纵向分布零件可靠度的计算模型。从模型的建立过程中可以发现,基于零件纵向分布的可靠度模型需要对各个时刻(或者不同载荷作用次数)的载荷概率密度函数进行统计。然而这在实际上是做不到的,因为这需要记录大量的载荷 -时间历程样本,并且进行大量的统计。为便于工程应用,往往假设载荷历程为各态历经过程,也即认为各个时刻的载荷概率密度函数相同。这对载荷-时间历程样本数目和时刻的选择提出了较高的要求,样本应该具有一定的代表性。更重要的是,当得到的载荷-时间历程样本数量不足,不能通过各个时刻的统计得到各态历经假设下的载荷概率密度函数,并且每个样本计数后拟合的概率密度函数相差比较大时,基于载荷横向分布的可靠度模型则可以充分地利用有限的样本直接对零件可靠度进行近似计算。

下面通过分析载荷横向分布和纵向分布概率密度函数的关系,给出在有限样本条件下,根据载荷的横向分布统计特性近似得到载荷纵向分布概率密度函数的方法,从而可以方便地使用基于载荷纵向分布的可靠度模型。这种方法避免了对样本进行各个时刻的统计,更适于利用传统可靠性模型进行计算。假设载荷历程为各态历经过程,每个时刻的概率密度函数相同,均为 f s(s)。那么每次载荷大小为s0的概率为P0=f s(s0)d s,该载荷不出现的概率为1-P0。如果载荷作用了n次(假设n足够大),那么该载荷出现的次数n0的期望值为E(n0)=nP 0=nf s(s0)d s。另外,在载荷作用的n次中,载荷s0出现次数为x的概率,即

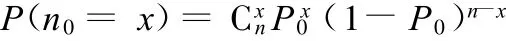
令P0为定值,对P(n0=x)取极值,得到 x=nP0=nfs(s0)d s。由此可以近似认为各个载荷-时间历程样本中,通过计数统计得到的出现概率最大的概率密度函数就是各态历经假设下载荷的纵向概率密度函数。或者分别求出各个样本中相同级别大小的载荷的平均出现次数,拟合出载荷的平均横向概率密度函数,并将其作为纵向概率密度函数。这样就可以结合载荷 -强度干涉模型,使用基于载荷纵向分布的可靠度模型计算零件及系统的可靠度。

假设不考虑强度退化,零件强度服从N(600,302)MPa的正态分布,载荷分布服从 N(500,302)MPa的正态分布,初始可靠度为1。当载荷的概率密度函数为纵向概率密度函数时,利用式(2)可以得到可靠度随载荷作用次数的关系。当载荷的概率密度函数为横向概率密度函数时,应用式(3)得到可靠度随载荷作用次数的变化规律。二者的对比如图1所示。

图1 可靠度随载荷作用次数变化规律

由图1可以看出,两种情况下零件可靠度随载荷作用次数的增加而下降。对于相同的载荷作用次数,当载荷的概率密度函数为横向概率密度函数时,零件可靠度小于概率密度函数为纵向概率密度函数时的可靠度,并且开始随着载荷作用次数的增加,其差值逐渐增大,当载荷作用次数较大,零件趋于失效时,其差值逐渐缩小。产生差值的原因是,纵向概率密度函数是横向分布中出现概率最大的概率密度函数或者是平均横向概率密度函数,但是出现概率并非绝对等于1。从图1中可以看出,二者在一定载荷作用次数范围内差值并不是很大,可以进行近似计算,并且能够反映出零件可靠度的基本变化规律。所以,当获得的载荷-时间历程样本比较少时,也可以采用以上提出的近似方法,使用基于纵向载荷分布的可靠性模型进行零件的可靠度计算。从另外一个角度讲,在本例中,如果假设基于载荷纵向分布的计算结果是准确值,那么基于载荷横向分布的计算结果就是估算值。而由之前的推导过程可以看出,与纵向分布概率密度函数相同的横向概率密度函数出现的概率最大。因此更加说明了在有限数目样本情况下使用基于载荷横向分布的可靠性模型进行近似估算的合理性。

5 考虑共因失效时基于载荷横向分布的系统可靠度分析

以上着重分析了基于载荷横向分布的零件可靠度计算模型,对于由零件组成的系统,可以根据系统结构功能函数求解系统的可靠度。本文着重分析考虑共因失效的系统可靠度。当系统多个零件受到相同载荷作用时,如果作零件相互独立的假设将引起较大的误差。目前,研究人员提出了很多考虑共因失效的可靠度计算模型,如α因子模型、β因子模型、BFR模型等。但是这些方法仍然基于元件层面,物理意义不明确[7-9]。本文直接应用之前建立的可靠度模型,分析当系统元件承受同一载荷多次作用时的可靠度变化规律。

为了叙述方便,以下均假设组成系统的零件相同,并且不考虑强度退化,每个零件具有相同的强度概率密度函数和分布函数f r(r)、Fr(r)。对于由a个零件组成的串联系统,当大小为确定值s的载荷作用一次时,系统可靠度为

假设载荷的横向分布概率密度函数为 f sj(s),特征概率密度函数为 f X(Xj),则利用与式(3)类似的推导过程,可以得到随机载荷作用n次后串联系统的可靠度：

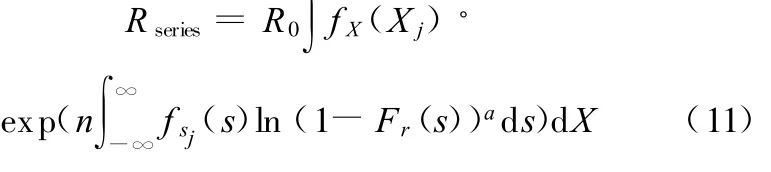
离散化模型为

同理,由a个零件组成的并联系统,当大小为确定值s的载荷作用一次时,系统可靠度为

随机载荷作用n次后并联系统的可靠度为

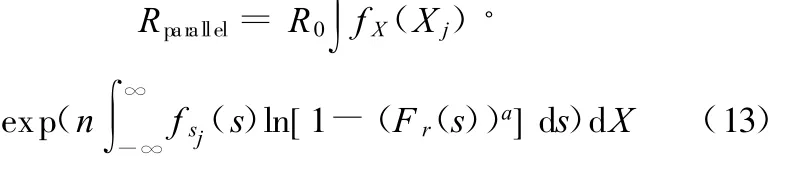
离散化模型为

由a个零件组成的k/a系统,当大小为确定值s的载荷作用一次时,系统可靠度为

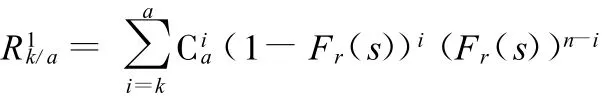
随机载荷作用n次后k/a系统的可靠度为

离散化模型为

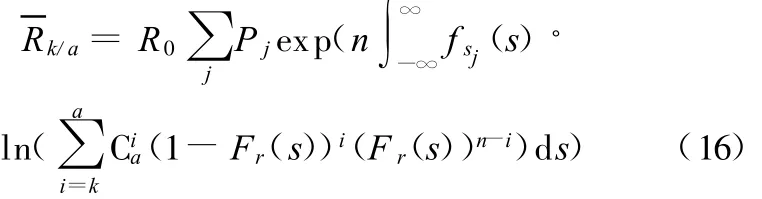
以上模型在建立的过程中考虑了零件承受的载荷为同一载荷这个信息,并且没有作零件相互独立的假设,因此反映了共因失效这种失效相关性。

以上分析了随机载荷作用下系统可靠度随载荷作用次数的变化规律。如果考虑载荷出现次数的随机性,则可以得到当强度退化时零件的时变可靠度计算模型。如果载荷出现的次数满足以下条件[10]：①当t=0时,n(0)=0;②在互不重叠的时间段内载荷出现的次数相互独立;③在时刻t和足够小的时间段Δt＞0,有

则时间t内出现n次载荷的概率为

也即将载荷出现的次数看作是强度为λ(t)的泊松过程。这时,由全概率公式,可以得到系统可靠度随时间的变化规律。假设系统初始可靠度为1。对于串联系统,由式(11)得到的系统可靠度为

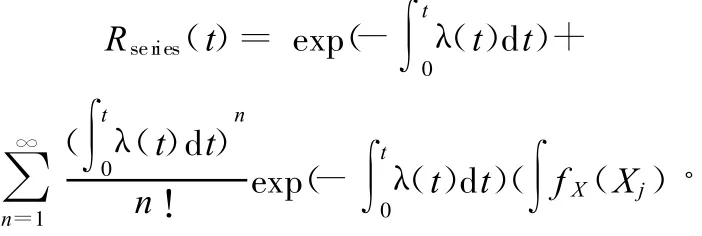
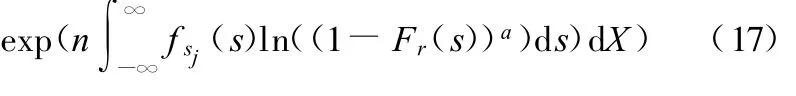
由式(13),得到并联系统的可靠度为

由式(15),得k/a系统的可靠度为

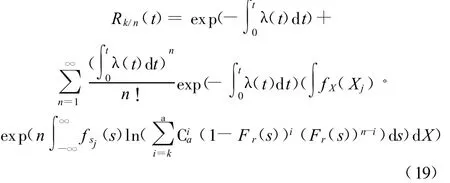
假设有分别由3个相同零件组成的串联系统、并联系统及2/3系统。对已得到的载荷-时间样本进行统计,得到的各个样本均服从双参数威布尔分布。特征参数的分布律如表1所示。λ(t)=0.6h-1,初始可靠度为 1,零件强度服从均值为650MPa、标准差为20MPa的正态分布,则零件可靠度随时间的变化规律如图2所示。

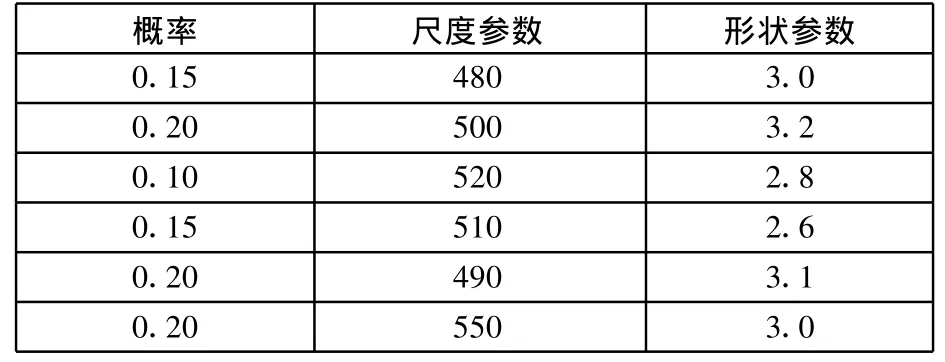
表1 载荷特征参数分布律

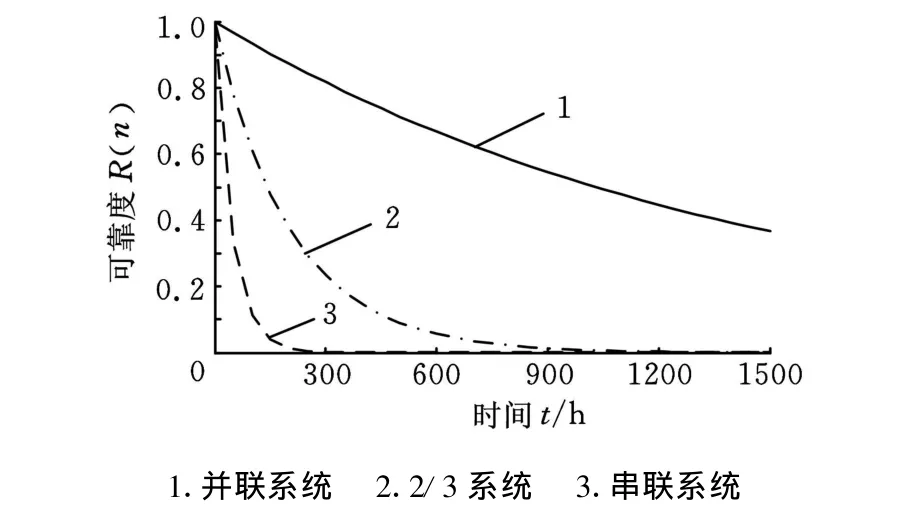
图2 可靠度与时间的关系

从图3可以看出,系统可靠度随时间逐渐降低,并且在初始阶段下降速度最快,随后下降速度趋于平缓。其中串联系统下降速度最快,可靠度最低,2/3系统其次,并联系统下降最慢。实际上该例中串联系统相当于1/3系统,并联系统相当于3/3系统,结果与实际相吻合。

6 结论

(1)机械零件及系统往往承受随机载荷的多次作用,在分析随机载荷下的零件可靠度时应该首先对随机载荷的统计特征进行分析。本文提出载荷的二维分布,也即载荷的横向分布和纵向分布。传统载荷-强度干涉模型适用于载荷作用一次的可靠度计算。在计算随机载荷指定作用次数后的可靠度时,应该使用载荷的纵向概率密度函数。但是,工程上得到的是载荷-时间历程样本。由于样本数量的限制以及载荷纵向分布统计特性获得的困难,使得基于载荷纵向分布的可靠性模型难以应用,因此,本文重点分析了基于载荷横向分布的可靠度计算模型。该模型可以直接根据获得的样本进行可靠度计算,并从理论上分析了该计算方法的合理性。

(2)本文在建立基于载荷的横向分布的计算模型时,分别考虑了强度退化以及强度不退化两种情况,可以应用于零件早期失效期(强度不退化或者退化不明显)以及偶然失效期和耗损失效期(需要考虑强度退化)。此外,通过分析载荷纵向概率密度函数与横向概率密度函数的关系,提出了根据载荷横向分布统计特征,近似得到各态历经假设下载荷纵向概率密度函数的方法,这样便可以结合载荷-强度干涉模型计算零件可靠度与载荷作用次数的关系。通过实例验证了该方法可以近似反映零件可靠度的变化规律,并同时从另一个角度验证了基于载荷横向分布的可靠性模型的合理性和正确性。

(3)由基于载荷横向分布的零件可靠度计算模型分析了几种典型机械系统的可靠度计算方法。传统的模型需要假设零件间相互独立,但实际上由于载荷的相关性,使得独立假设往往不能反映系统的实际可靠度。本文没有作零件相互独立的假设,直接根据系统中零件的组成结构推导出串联系统、并联系统以及表决系统的可靠度计算方法。本文进一步考虑了载荷作用次数的随机性,通过假设载荷作用次数为泊松过程,建立了系统的时变可靠度计算模型。

[1] Huang W,Askin RG.A Generalized SSI Reliability M odel Considering Stochastic Loading and Strength Aging Degradation[J].IEEE Transaction on Reliability,2004,53(1)：77-82.

[2] Koh C G,Ang K K,Zhang L.Effects of Repeated Loading on Creep Deflection of Reinforced Concrete Beams[J].Engineering Structures,1997,19(1)：2-18.

[3] Thayalan P,Aly T,Patnaikuni I.Behaviour of Con-crete-filled Steel Tubes Under Static and Variable Repeated Loading[J].Journal of Constructional Steel Research,2009,65：900-908.

[4] 王正,谢里阳,李兵.随机载荷作用下的零件动态可靠性模型[J].机械工程学报,2007,43(12)：20-25.[5] 王新刚,张义民,王宝艳.载荷作用次数和强度退化对SSI模型的影响[J].机械设计与制造,2008,(12)：205-207.

[6] Freudenthal A M.Safety of Structures[J].Transaction,ASCE,1947,112：125-180.

[7] Levitin G.Incorporating Common-cause Failures into Nonrepairable Multistate Series-parallel System Analysis[J].IEEE Transaction on Reliability,2001,50(4)：380-388.

[8] Xie L Y,Zhou J Y,Hao CZ.System-level Loadstrength Interference Based Reliability Modeling of k-out-of n System[J].Reliability Engineering and System Safety,2004,84：311-317.

[9] Xie L Y,Zhou JY,Wang Y Y,et al.Load-strength Order Statistics Interference M odels for System Reliability Evaluation[J].International Journal of Performance Engineering,2005,1(1)：22-36.

[10] 李裕奇,刘赪,王沁.随机过程[M].北京：国防工业出版社,2008.