微位移机构中变截面柔性铰链等效刚度的求解方法研究
2010-06-04刘庆玲翁海珊邱丽芳
刘庆玲 翁海珊 邱丽芳
1.北京科技大学,北京,100083 2.廊坊师范学院,廊坊,065000
0 引言
柔性机构利用柔性铰链的弹性变形实现运动的传递,具有无摩擦、无间隙、运动灵敏度高的特点,在微机电、航空航天、机器人等众多领域获得了广泛的应用[1]。对柔性机构变形特性的分析,目前大多采用以下方法:基于铰链柔度的计算方法[2],但分析过程复杂且计算量大;伪刚体模型法,伪刚体模型中柔性铰链等效刚度k的确定是一个关键问题[3]。柔性机构中广泛应用的直梁形形[4]、导角形[5]、椭圆形等各种变截面柔性铰链以其各自的优势在柔性机构中也获得了广泛的应用[6]。由于铰链厚度的变化,采用最小厚度或平均厚度近似计算[7]其等效刚度,无疑会导致误差的产生。因此,合理确定变截面柔性铰链的等效刚度k是十分必要的。本文对此作了分析,给出了两种求解方法,并将其应用于微位移放大机构的分析中。
1 变截面柔性铰链等效刚度的确定
任意变截面柔性铰链的结构示意图及符号意义如图1所示。铰链的最小厚度、两端的厚度即铰链的最大厚度分别用t、h表示。
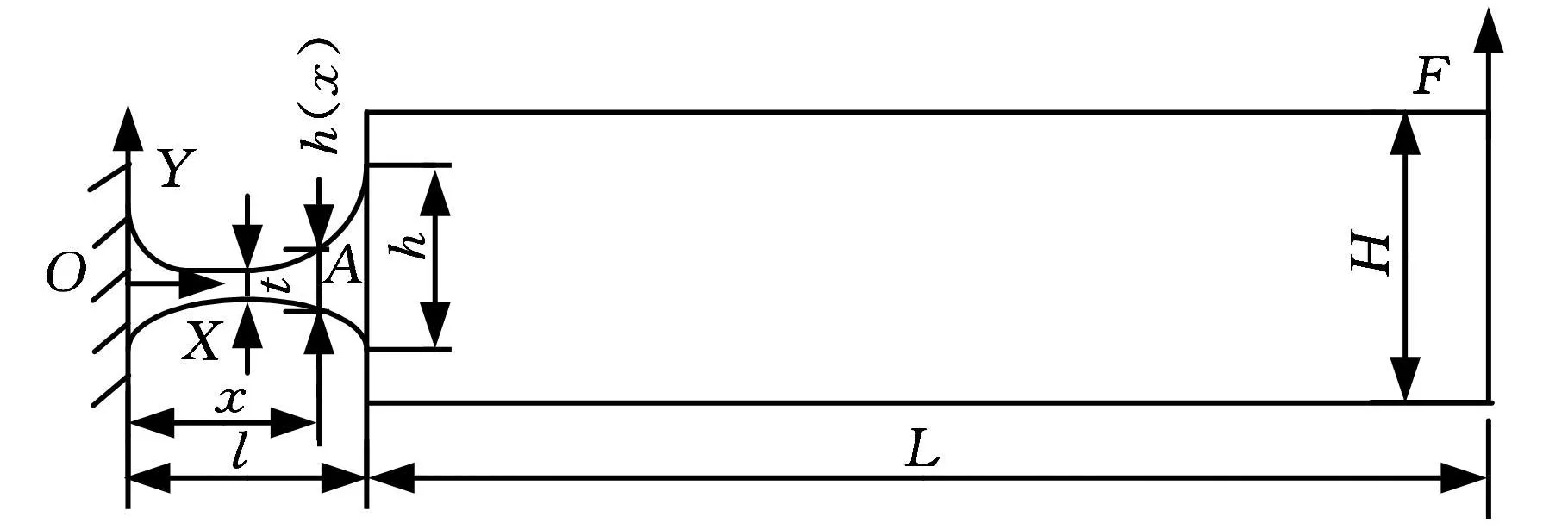
图1 带有变截面柔性铰链的柔性构件结构示意图
1.1 修正系数法
由于柔性铰链的厚度连续变化,本文提出了等效厚度的概念,记为h,以此来计算变截面柔性铰链的等效刚度。为此,作如下定义:

(2)定义变截面柔性铰链的等效厚度h,且约定h=μh,其中h 为变截面柔性铰链的平均厚度;μ为修正系数,取决于柔性铰链本身的结构特性。
以圆弧型变截面柔性铰链为例,材料选用铍青铜,弹性模量E=126GPa,其最小厚度t分别取0.4mm、0.5mm、0.6mm 、0.8mm;改变铰链的最大厚度 h,使其满足h/t=2,3,…,12;铰链长l=8mm;杆件参数:H=10mm,L=60mm;柔性构件宽度b=20mm。采用如下方法获得一系列相应的修正系数μ。
(1)采用有限元分析法分析柔性构件的变形,其有限元模型如图2所示。在柔性构件末端施加不同载荷,得到柔性构件末端角变形的大小,借助伪刚体模型法的相关理论,反推求得一个对应的铰链厚度值h。
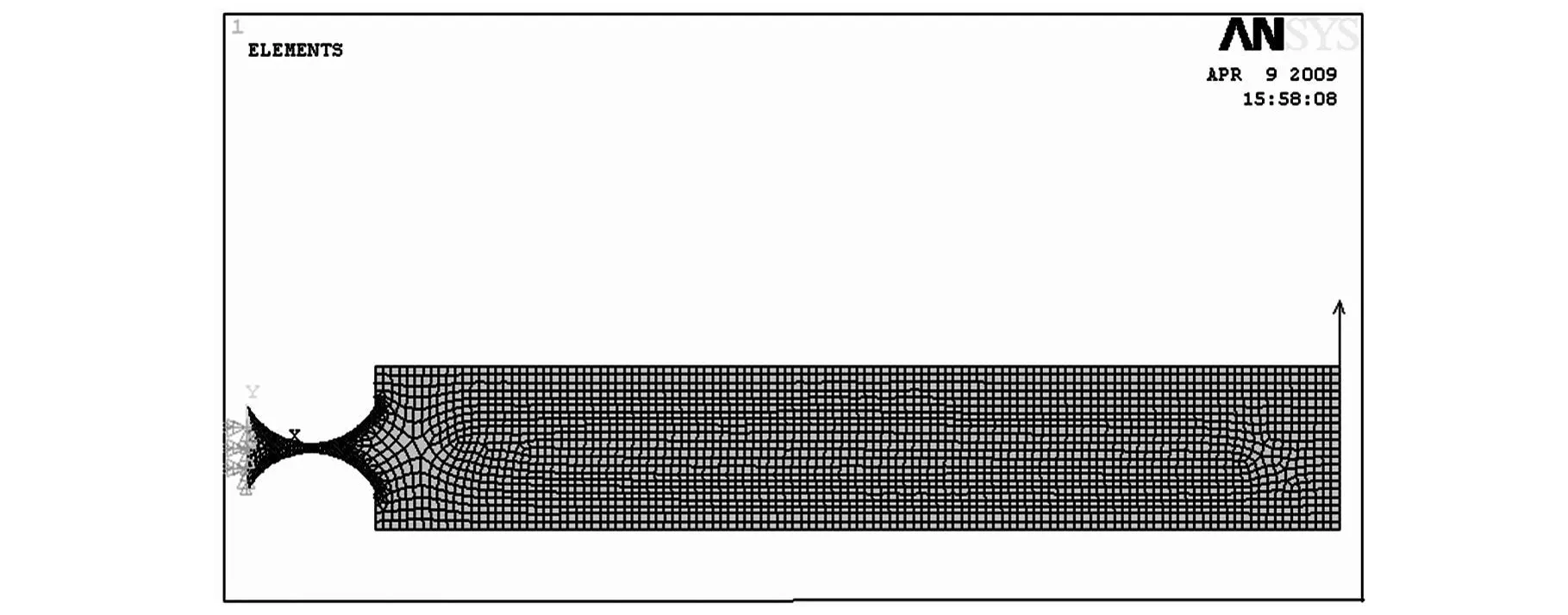
图2 柔性构件的有限元模型(t=0.5mm,h=5mm)
(2)计算变截面柔性铰链的平均厚度h:
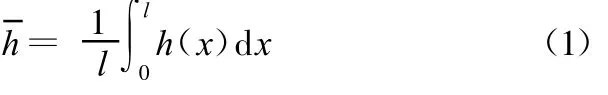
通过h与h 之比,得出修正系数 μ值,经过多组实例的计算,取其平均值,得到修正系数的经验数值,列于表1。
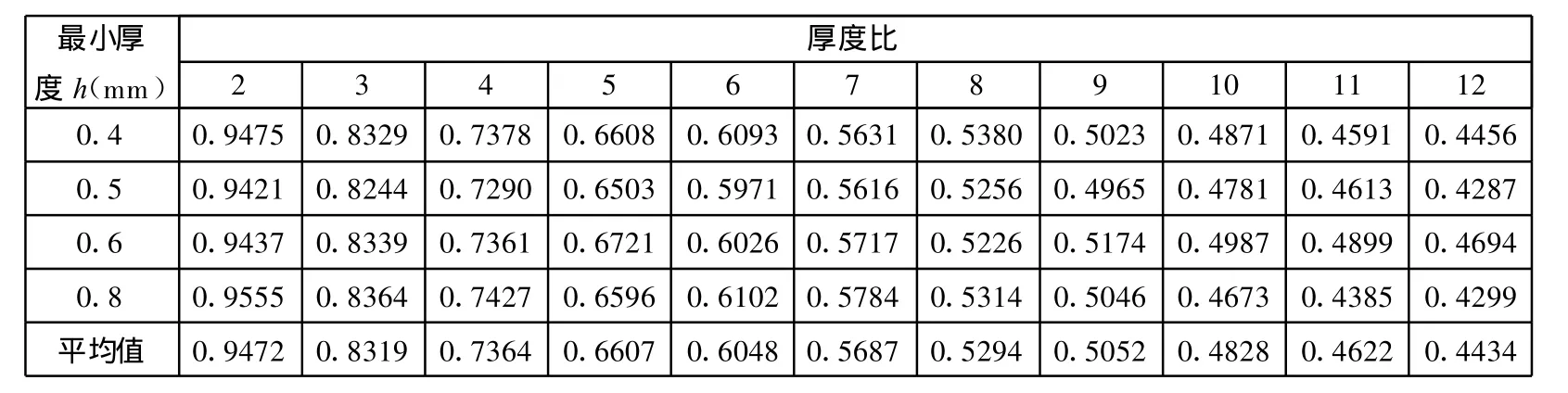
表1 修正系数μ的经验值
对于表1中的数据,以αh为自变量,对其进行曲线拟合,结果如下:

利用上述方法,得到一系列修正系数μ,对变截面柔性铰链的平均厚度h 进行修正,得到变截面柔性铰链的等效厚度h,以此计算铰链的等效刚度k,即
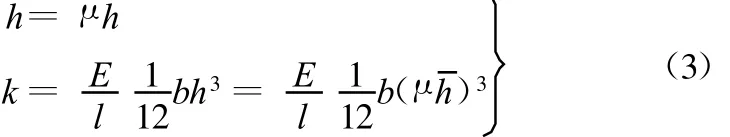
1.2 变截面法
对于图1所示的任意变截面柔性铰链,充分考虑其截面的变化,依据材料力学中梁的基本变形方程,采用积分的方法求得等效刚度。取距固定端距离为x的任意截面A,设该处铰链的厚度为h(x),对该截面A进行受力分析,可得截面处的力矩为
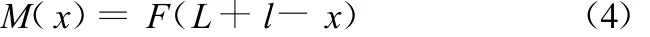
根据材料力学中梁的基本变形方程:
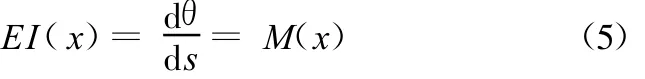
考虑小变形,将式(4)代入式(5),可求得柔性铰链的角变形θ为
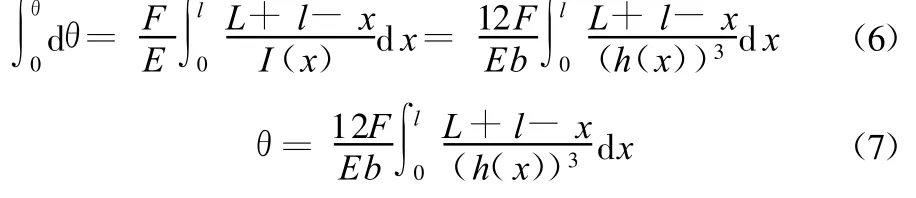
由伪刚体理论,有
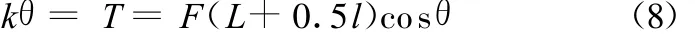
将式(7)代入式(8),可得
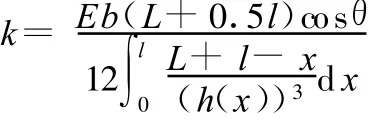
考虑小变形,cosθ≈1,可得
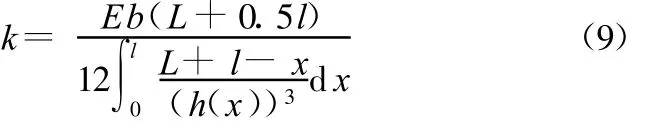
利用上述方法,确定了变截面柔性铰链的厚度表达式h(x),即可由式(9)求得不同类型、不同结构尺寸的变截面柔性铰链的等效刚度k。
1.3 两种方法的对比
带有圆弧型柔性铰链的柔性构件,给定几何参数如下:l=8mm,h=3mm,H=10mm,L=60mm,宽度b=20mm,铰链最小厚度t分别取0.4mm 、0.5mm、0.6mm,设变截面柔性铰链对应的等效刚度k分别为k 1、k2、k3,采用两种方法进行求解。
(1)修正系数法。给出的3个变截面柔性铰链,其特征厚度比分别为:αh1=7.5;αh2=6,αh3=5,由表1结合式(3)求得的各修正系数μ分别为0.5422、0.6048、0.6607。用式(2)求得平均厚度,对其进行修正。由式(4)求得的k值分别为:k1=7.0289,k2=12.3564,k3=19.7756。
(2)变截面法。将各变截面柔性铰链的参数分别代入式(9),得到k1=6.981,k2=12.0344,k3=19.2791。
由计算结果可以看出,两种方法的结果基本一致。但是比较而言,修正系数法中的μ值随变截面柔性铰链的结构、尺寸的变化而变化,需要通过大量算例反推而求得,该方法繁琐且耗时,不具有通用性,且计算精度不高;而变截面法直接利用铰链的几何特征,计算过程简单,精度高,具有一定的通用性。
2 变截面法在微位移机构中的应用
柔性铰链八杆微位移放大机构如图3所示,8个圆弧形柔性铰链大小相同,对称设计,下端固定。在机构两侧 A、B处对称施加水平方向的载荷,通过两侧收缩(或扩张)产生输入位移,利用柔性铰链的弯曲变形,获得与输入方向垂直的输出位移,以及机构的放大比。该机构材料为单晶硅,弹性模量为 169GPa,整个机构的宽度为75μm,该机构双向对称,相关几何尺寸如图3所示。下面分析该机构在不同载荷作用下的输入、输出位移及其放大比。

图3 柔性铰链八杆微位移放大机构示意图
2.1 变截面法理论计算
将图3中相关几何尺寸代入式(9),求得的各柔性铰链等效刚度均为4.1033×10-5,在此基础上,依据伪刚体理论,对该柔性铰链八杆微位移放大机构进行分析,求得该机构在水平载荷作用下的输入位移、输出位移及其放大比。求解结果如表2所示。
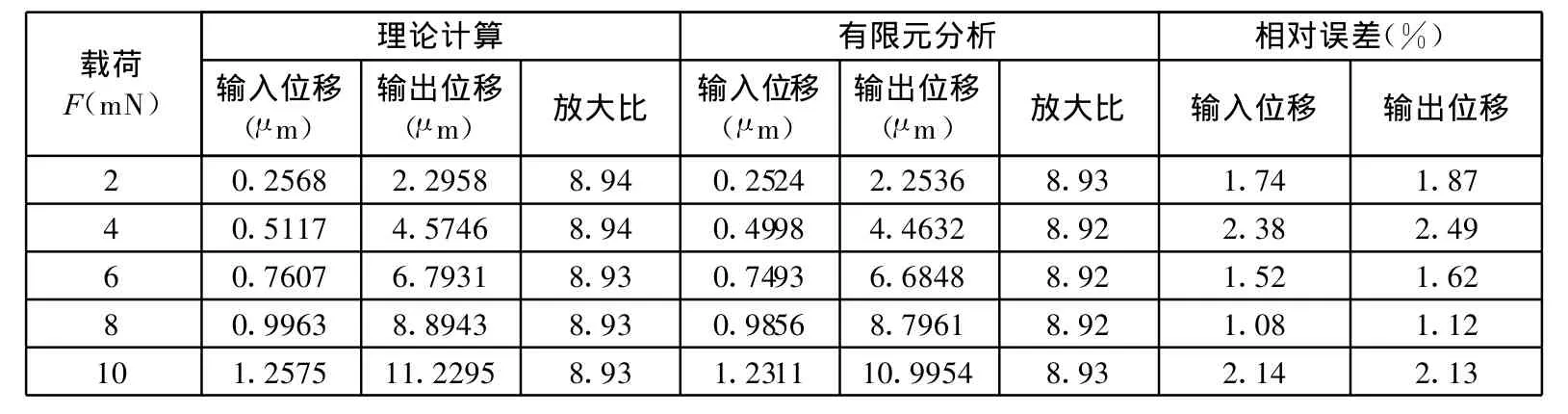
表2 柔性铰链八杆微位移放大机构理论计算与有限元分析的结果对比及相对误差
2.2 有限元法仿真分析
在ANSYS环境下,选取Solid45单元类型,建立相同结构尺寸的柔性微位移放大机构的有限元模型,如图4所示。对机构底部施加约束,在其两侧的中部对称施加水平载荷,分析机构在不同载荷作用下的输入、输出位移,进而求得放大比。有限元的分析结果列于表2。

图4 柔性铰链八杆微位移放大机构的有限元模型
2.3 结果对比分析
由表2数据可明显看出,采用变截面法计算柔性铰链的等效刚度,进而求得微位移机构的输入、输出位移以及放大比,所得结果与有限元法的分析结果基本一致,其输入位移、输出位移的相对误差均在2%左右。引起误差的主要原因有:机构在进行简化过程中会产生一定误差,杆并非理想刚性杆,存在一定变形;在计算机仿真时,由于角变形很小,利用弦长代替弧长计算,也是造成误差的一个原因。
3 结论
针对变截面柔性铰链等效刚度k值的计算进行了研究,给出了两种求解方法:修正系数法与变截面法。比较而言,变截面法具有通用性,而且计算简便。采用变截面方法计算了柔性铰链八杆微位移放大机构中圆弧型柔性铰链的等效刚度k,在此基础上,依据伪刚体理论分析了该微位移机构的变形,将求解结果与有限元法的分析结果相对比,二者具有较好的一致性,验证了k值计算的正确性。
[1] 于靖军,宗光华,毕树生.全柔性机构与M EMS[J].光学精密工程,2001,9(1):1-5.
[2] 张志杰,袁怡宝.典型柔性铰链柔度性能的计算与分析[J].工程力学,2008,25(4):106-110.
[3] Midha A,Howell L L,Norton T W.Limit Positions of Compliant Mechanisms Using the Pseudo-right-body Model Concept[J].Mechanism and Machine Theory,2000,35(1):99-115.
[4] Yong Yuenkuan,Lu Tienfu,Handley D C.Review of Circular Flexure Hinge Design Equations and Derivation of Empirical Formulations[J].Precision Engineering,2007,5:1-8.
[5] Lobontiu N,Paine J S N.Corner-filleted Flexure Hinges[J].Mechanical Sign,2001,123:346-352.
[6] Yong Yuenkuan,Lu Tienfu.The Effect of the Accuracies of Flexure Hinge Equations on the Output Compliances of Planar Micro-motion Stages[J].Mechanism and Machine Theory,2008,43(3):347-363.
[7] Wu Yingfei,Zhou Zhaoying.Design Calculations for Flexure Hinges[J].Preview of Scientific Instruments,2002,73(8):3101-3106.
