基于无应力状态法的零杆虚位移修正

田维锋，周水兴，秦 镇

（1.重庆大学土木工程学院，重庆 400045;2.重庆交通大学土木建筑学院，重庆 400074;3.重庆公路工程质监站，重庆 400060）

基于无应力状态法的零杆虚位移修正

田维锋1，2，周水兴2，秦 镇3

（1.重庆大学土木工程学院，重庆 400045;2.重庆交通大学土木建筑学院，重庆 400074;3.重庆公路工程质监站，重庆 400060）

分析了大跨径斜拉桥施工控制和结构分析中零杆虚位移的成因及其导致的计算误差，提出了基于无应力状态法理论的误差修正方法。通过算例验证，表明该方法是有效的，对于桥梁的有限元误差分析具有一定参考价值。

零杆单元;无应力状态法;虚位移;切线安装;误差修正

大跨度斜拉桥在整个施工过程中，结构体系、荷载、约束条件等都在不断发生变化，是一个复杂的非线性的过程，其中几何非线性因素最为明显。无应力状态法［1-4］是大跨径斜拉桥施工状态分析的一种方法，已在多座斜拉桥的的施工中得到了成功应用。无应力状态法指出无应力状态量（结构无应力曲率、无应力长度）是结构的固有特性，是结构任何两个状态的内在关系。对于一个线弹性结构，只要单元无应力状态量、外荷载和边界条件一定时，最终成桥结构的内力状态和位移状态与结构的形成过程和施工方法无关。

在大跨径斜拉桥施工分析中，通常利用有限元软件ANSYS的生死单元功能模拟节段安装，同时利用APDL二次开发工具编制命令流使得桥梁的施工模拟分析更加程序化、简单化［5-7］。在实际分析中，由于有限元模型存在零杆虚位移的影响，导致单元的无应力状态量发生改变，从而产生计算误差。

笔者结合算例，分析了零杆虚位移及其误差的成因，并应用无应力状态法理论进行误差修正，给出了相应的算法。

1 零杆虚位移及计算误差

在施工分析中，零杆单元通常用于模拟斜拉桥中未安装的主梁节段或拉索，在正装时逐个激活，模拟节段的安装。零杆单元的实质是单元的刚度矩阵K、质量矩阵M乘以一个很小的因子（如在ANSYS中缺省值为1.0e-6），单元本身并没有被从模型中删去，仍处于模型当中。在正装分析过程中，逐个激活零杆单元并不是将其到模型中，而是在上一个施工阶段计算完成后的零杆位置上，将其刚度、质量、单元荷载等将恢复其建模时的数值。激活的单元无应变记录，是无应力状态的单元。考虑到几何非线性的影响，在分析过程中要打开ANSYS的大变形效应［NLGEOM，ON］［8］。在每个荷载步聚计算结束后，零杆单元会偏离其建模时的位置，产生零杆虚位移。

利用ANSYS建立斜拉桥结构有限元模型（图1、图2），说明“零杆虚位移”的产生机理及其所导致的计算误差。模型共有节点8个，单元11个。主梁和主塔单元截面2 m×2 m，弹模3.5×104MPa，采用BEAM 188梁单元;斜拉索单元截面积0.005 m2，弹模2.1 ×105MPa，采用link 8杆单元，塔梁固结，用降温模拟拉索张拉，在主梁节点各施加2 000 kN的竖向集中力，不计自重及材料非线性。分别按照分阶段施工和一次成桥计算进行分析。

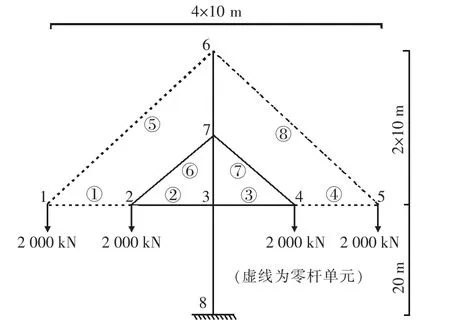
图1 施工阶段ⅠFig.1 Construction phaseⅠ

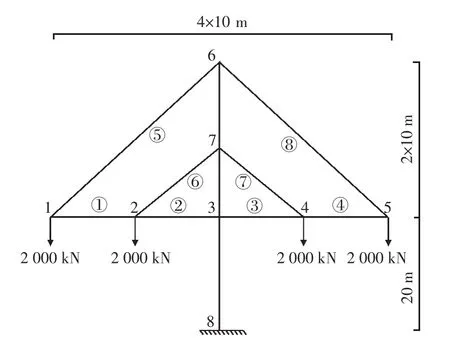
图2 施工阶段ⅡFig.2 Construction phaseⅡ

1）施工阶段Ⅰ（图1）:激活主塔及第一节段的主梁单元（②、③）及第一对拉索单元（⑥、⑦），在2#、4#节点施加2 000 kN的竖向力;

2）施工阶段Ⅱ（图2）:激活第二节段的主梁单元（①、④）及第二对拉索单元（⑤、⑧），同时在1#、5#节点施加2 000 kN的竖向力。

考虑到结构的对称性，取半跨结构各施工阶段和一次成桥的结构位移（u:水平位移、v:水平位移、α:转角位移）、拉索参数（l0:几何模型索长、Δl:伸长量、N:索力）及内力见表1～表3。

由表1可以看出，在施工阶段Ⅰ时，主梁单元（①）、拉索单元（⑤）为零杆单元时，单元上没有内力，但其节点（1#节点）仍有位移位（u11=0.093 59 mm、v11=32.171 mm），即为零杆虚位移。该位移是由零杆单元与其他激活单元共同参与整个有限元模型的计算时在零杆上产生的位移。

表1 结构位移Tab.1 Structural displacement

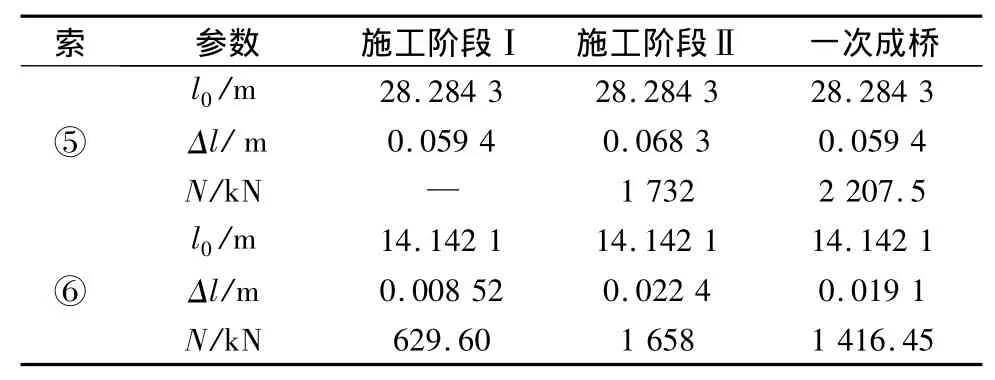
表2 拉索参数Tab.2 Cable parameters

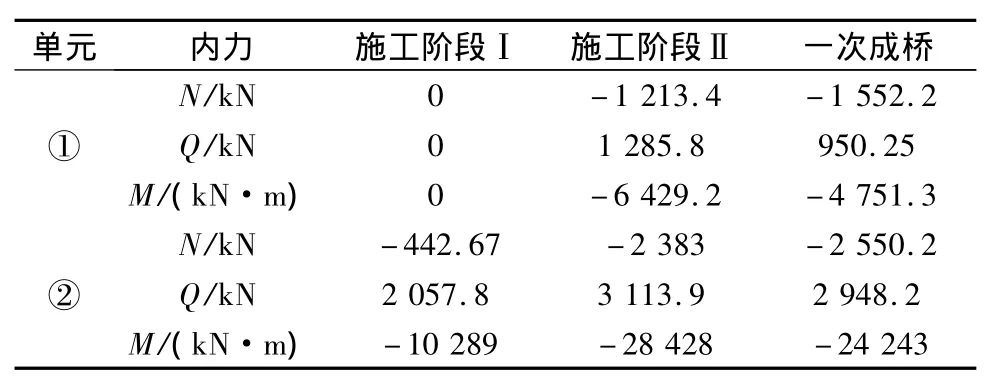
表3 结构内力Tab.3 Structure forces

由于拉索是线弹性单元（未考虑拉索的垂度），索力N与伸长量存在如式（1）的关系。

式中:E为拉索弹模，E=2.1×105MPa;ε 为 Δl/l0;A为拉索截面积，A=0.005 m2

在表2，拉索单元（⑤），在施工阶段Ⅰ、Ⅱ时，索力N与伸长量均满足式（1）。施工阶段Ⅱ时，拉索单元（⑤），伸长量按式（1）计算的索力 N=2 535.36 kN与表2计算索力（1 732 kN）有较大的误差。

在表2、表3中，分阶段施工和一次成桥计算所得的拉索索力与结构内力值也存在较大的差异。

2 误差分析

根据无应力状态法理论，无应力状态量是结构的固有特性，如果没有对结构本身变动，这种特性是不会改变的。只要最终成桥的塔、梁单元无应力曲率、拉索单元的无应力长度、外荷载和边界条件一定时，最终成桥结构的内力状态和位移状态与结构的形成过程和施工方法无关，即无论是分阶段还是一次成桥，最终结构的内力、变形应为一致。由此可见，上述中的计算误差是由结构的无应力状态量发生改变所致。

2.1 索无应力长度的改变

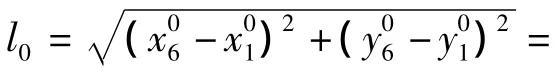
2.2 单元的无应力曲率的改变

节段安装的桥梁结构，主梁单元的无应力曲率是节段在设计的几何线形曲率，为保证主梁的无应力曲率不改变，要求在施工和有限元计算中及在节段的切线位置安装下一个节段。以悬臂结构为例，如图3。施工阶段I计算完成后，①单元1#节点发生位移，变形至1′点。为了保证模型的无应力曲率不变，②单元应位于1′点的切线位置，即要求线段1′2′的斜率应与 1′处（1#节点变形后位置）的切线斜率相等，并在下一个施工阶段时，在此位置激活。

图3 切线安装示意图Fig.3 Tangent installation diagram

在斜拉桥算例中，施工阶段I完成后，2#节点变形后的切线曲率为0.002 20，1#节点产生了虚位移

3 误差修正

在有限元进行桥梁施工分析时，零杆虚位移是不可避免的，为了修正由此产生的计算误差，必须保持结构的无应力状态量不发生改变。在施工计算时，为了保证单元的无应力曲率保持不变，要求新的节段安装即零杆单元激活时，应处于前一个单元的切线安装位置上。在此基础上计算出索的零杆长度，通过对索施加温度荷载，使其缩短（或伸长）至原始无应力索长。由于是针对零杆单元进行的修正，故不会对已安装（激活）的单元产生影响。

上述方法可以方便地用ANSYS的APDL语言编制命令流来实现。考虑结构的对称性，以半跨斜拉桥模型（图4）说明相应算法如下:

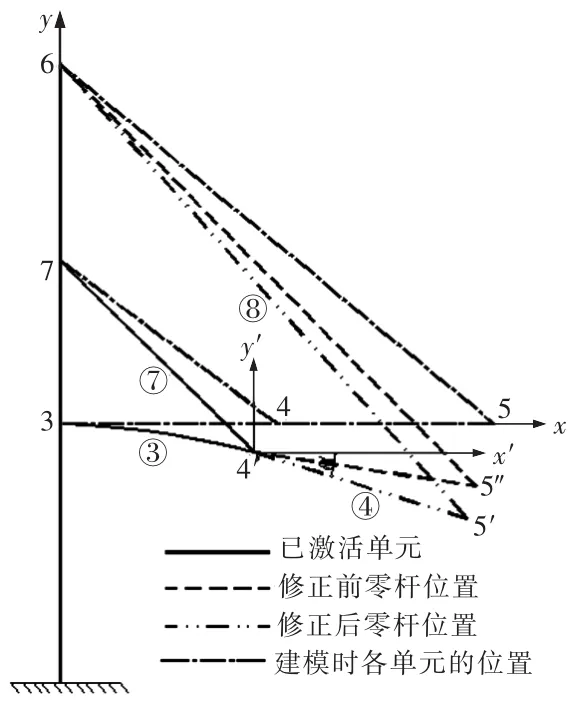
图4 零杆单元位置修正计算图示（半跨）Fig.4 Modification of virtual displacement（semi-cross）

1）建立斜拉桥全桥有限元模型，杀死所有单元。

2）施工主塔、安装第一节段主梁及第一对拉索。在有限元模型中激活相应的单元（③、⑦），并计算。5″为本阶段计算完成后零杆单元（④）右节点实际位置，由于存在零杆虚位移的影响，该点没有按照切线安装的要求位于5′。

3）计算前一个单元右节点 4′坐标（X′4，Y′4）。在图4中③单元为已激活的主梁单元，在本荷载步计算完成后可以获得该单元右节点（4#）的位移，ΔX′4，ΔY′4及转角位移 Δα4。

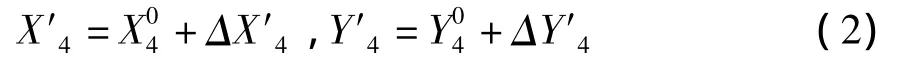
4）计算下节段（④）切线安装时右节点5″的坐标，

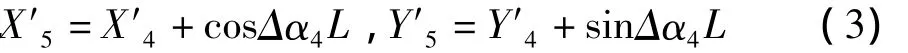
式中:L为第二节段（④）的无应力长度，即该单元的几何长度。

5）计算第二节段（④）切线安装右节点5′的位移，

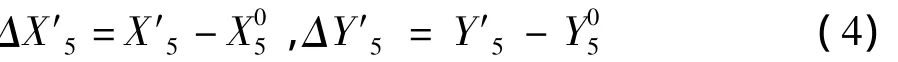
6）计算零杆索长L65′，无应力索长温度修正值ΔT:

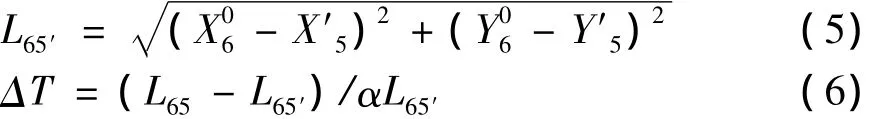
7）对零杆单元（④）的右节点（5#）施加强迫位移 ΔX′5，ΔY′5。

8）安装第二节段主梁及第二对拉索并张拉。在有限元模型中在切线安装位置激活相应的单元（④），对拉索（⑧）施加ΔT的温度荷载。

按照上述步骤进行零杆虚位移修正后，施工阶段Ⅱ的结构位移（u:水平位移、v:水平位移、α:转角位移）、拉索参数（l0:几何模型索长阶段、Δl:伸长量、N:索力）及内力见表4～表6。

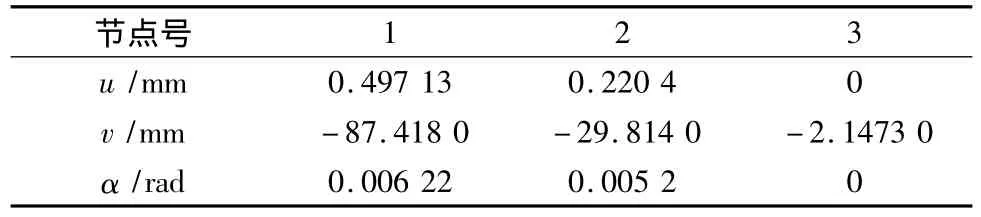
表4 结构位移Tab.4 Structural displacement

表5 结构内力Tab.5 Structure forces

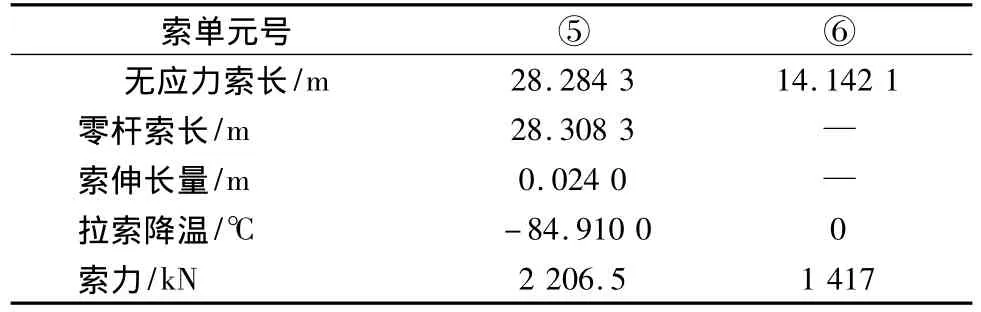
表6 拉索参数Tab.6 Cable parameters

经过上述修正，保证了结构的无应力状态量在计算过程中没有发生改变，比较表1～表6中数据，可见修正后施工阶段Ⅱ与一次成桥的主梁内力、拉索索力、位移吻合良好。

4 结论

在大跨度斜拉桥施工分析中，零杆虚位移导致了结构无应力状态量发生改变，从而引起了计算误差。笔者运用无应力状态法理论，编制APDL语言命令流，修正了零杆虚位移引起的无应力状态量改变，保证了计算结果的正确。通过算例验证，这种修正方法是可行的。

［1］ 秦顺权.斜拉桥安装无应力状态控制法［J］.桥梁建设，2003（2）:31-34.

［2］ 秦顺权.分阶段施工桥梁的无应力状态控制法［J］.桥梁建设，2008（1）:8-14.

［3］ 秦顺权.无应力状态控制法——斜拉桥安装计算中的应用［J］.桥梁建设，2008（2）:13-16.

［4］ 秦顺权.桥梁施工控制——无应力状态法理论与实践［M］.北京:人民交通出版社，2007.

［5］ 杨丽，王新敏，李义强.施工过程分析在ANSYS中的实现［J］.国防交通工程与技术，2006（3）:64-65.

［6］ 颜毅，杜鹏.桥梁施工过程分析在ANSYS中的实现方法 ［J］.重庆交通大学学报:自然科学版，2007，26（5）:18-21.

［7］ 张立明.Aglor、Ansys在桥梁工程中的应用方法与实例 ［M］.北京:人民交通出版社，2003.

［8］ 尚晓江.ANSYS结构有限元高级分析方法与范例应用［M］.北京:中国水利水电出版社，2006.

Modification of Virtual Displacement Based on Unstressed State Method

TIAN Wei-feng1，2，ZHOU Shui-xing2，QIN Zhen3
（1.School of Civil Engineering，Chongqing University，Chongqing 400045，China;
2.School of Civil Engineering ＆ Architecture，Chongqing Jiaotong University，Chongqing 400074，China;
3.Chongqing Highway Engineering Quality Supervision Station，Chongqing 400060，China）

The causes of virtual displacement in long-span cable-stayed bridge construction control and structural analysis have been analyzed.The calculation errors which are resulted from the virtual displacement have also been described.The error modification method based on unstressed state theory is proposed.The effectiveness of the modified method has been verified through examples.The proposed method is of reference value for FEM error analysis of bridge.

death element;unstressed state method;virtual displacement;tangent installation;error modification

U448.27;U445.1

A

1674-0696（2010）01-0020-03

2009-07-09

重庆市交委重点科研项目（WFKY-003-40117）

田维锋（1976-），男，重庆市人，讲师，博士研究生，主要研究领域为大跨度桥梁设计与结构非线性分析。Email:zylgghnt@126.com。