文献半衰期与普赖斯指数之间的关系研究

陈京莲，胡 玮

（井冈山大学，吉安 343009）

1 引言

文献半衰期（half-life of literature）和普赖斯指数（Price indes）[1]是用来测度文献老化速度和程度的两个重要指标。Burton和Kebler将文献的半衰期定义为这样一段时间：在此时间内已发表的某一学科领域内正在被利用的全部文献中较新的一半,或目前所利用的文献中较新的一半是在多长时间内发表的。[2]普赖斯指数是指在某一知识领域内，把对年限不超过5年的文献的引文量与引文总量之比当作指数，用以量度文献的老化速度。当前，文献半衰期的计算方法有多种，也有不少文献对此问题进行了论述。其中应用广泛的方法有：（1）作图法：根据统计数据制成引文频次分布表，以纵坐标表示引文累积量或引文百分累积量，以横坐标表示被引文出版的年龄。从制得的图中在横坐标里找出与纵坐标上引文累积量或百分累积量一半处的对应点即为所求的文献半衰期；（2）公式法：公式法有负指数公式[3]、Burton和Kebler文献老化方程（简称为B-K方程）、莫蒂列夫（B.M.MOTIЛeB）修正公式和Pauline法[4]；（3）插值法。其中以莫蒂列夫修正式法和插值法最为常用。但我们在实际应用中发现莫蒂列夫修正式存在一定的局限性，即对于半衰期小于3年的学科（专业），该公式不适用，只能利用插值法。此外，现在人们在研究文献老化时主要是用文献半衰期和普赖斯指数作为衡量文献老化的速度和程度，但还没有见到有文献把这2个量度指标联系起来讨论文献的老化问题。

本文的目的主要有三个，首先我们从文献老化的B-K方程出发，得出文献半衰期与普赖斯指数之间的关系式；然后用此文献半衰期公式对文献[5]的数据进行拟合，并与插值法的结果进行比较，判断该计算公式是否合理；再用该计算公式计算的结果与B-K方程和莫蒂列夫修正式的文献半衰期计算方法计算的结果进行比较，判断这3种计算文献半衰期方法的优点和存在的局限性。

2 文献半衰期计算的新方法

Burton和Kebler文献老化方程 [1]，其形式如下：

式中的x是时间，以10年为单位；y是经过时间x时该学科总的引文比率，所以，1-y是时间x以外的引文比率。

Burton和Kebler文献老化方程的莫蒂列夫修正式为：

如果以PJ为某学科（专业）文献的普赖斯指数，由普赖斯指数的定义我们可以利用（1）式得到普赖斯指数与系数a之间的关系式为：

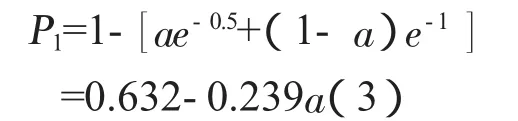
由（3）式就可以得到系数a与普赖斯指数之间的关系为：

如果以T1/2为某学科（专业）文献的半衰期，则由（1）式可得其文献的半衰期为：

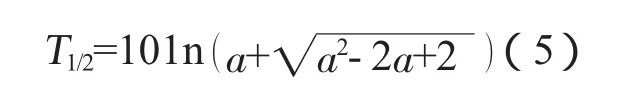
（5）式就是B-K方程的文献半衰期计算公式。联合（4）式和（5）式，可得到文献半衰期与普赖斯指数之间的关系为：

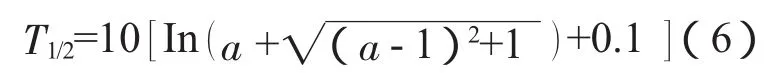
（6）式就是计算科技文献半衰期的新方法。由（6）式可知，我们只要知道科技文献的普赖斯指数就可以计算出该科技文献的半衰期。

而由（2）式可得莫蒂列夫修正式的文献半衰期计算公式为：

3 结果与讨论

为验证（6）式的合理性，我们用（6）式计算超导专业期刊文献的半衰期（见表1）。

由表1可知，最接近50%的引用累积百分比是在1989年，此年的引用累积量达到42.4%，距离统计当年（1990年）为2年，由插值法可知文献半衰期为2.32年。

由表1的数据，并由普赖斯指数的定义可知距离统计当年（1990年）之前5年，即1986年时的普赖斯指数为0.807，则由（6）式可计算出该刊的文献半衰期为：

同样，我们可以利用表1的数据，并由B-K方程可以计算出（1）式中系数a的值为0.082，则由（5）式可以计算出该刊的文献半衰期为：

我们还可以利用表1的数据，并由莫蒂列夫修正式可以计算出（2）的系数a的值为-0.246。则由（7）式可以计算出该刊的文献半衰期为：

表1 超导专业期刊引文数量分布[9]

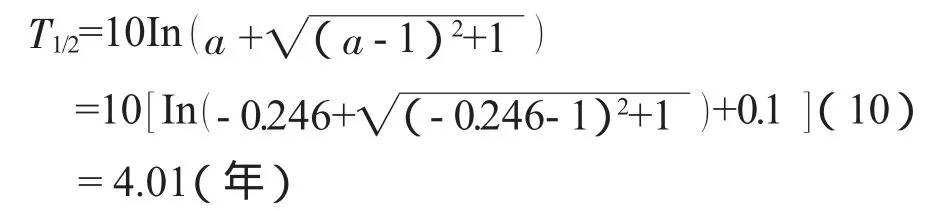
由上面的计算可知，如果以内插法的计算结果作为超导专业期刊的文献半衰期，则（8）式与此计算结果之间的相对误差低于2.2%，而（9）式与插值法计算结果之间的相对误差约为50%，（10）式与插值法计算结果之间的相对误差为72.8%。这表明用B-K方程的半衰期计算公式和莫蒂列夫修正式的计算文献半衰期公式在计算超导专业期刊上的文献半衰期有较大的误差。

此外，由（6）式可知，当 0≤P1≤1 时，所计算的文献半衰期的区间为：

这表明引文半衰期计算新方法所给出的文献半衰期的区间在T1/2∈[1.74，15.2]年，即它可以描述范围是半衰期为1.74-15.2年的学科或专业。

由（5）式可知，当0≤a≤1时，所计算的文献半衰期的区间为：

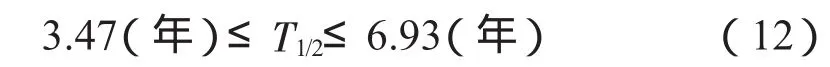
这表明由B-K方程的引文半衰期计算方法所给出文献半衰期的区间在T1/2∈[3.47，6.93]年，即它可以描述范围是半衰期为3.47-6.93年的学科或专业。

对莫蒂列夫修正式而言，假设系数a的取值范围在-0.5≤a≤1，则由（7）式计算的文献半衰期的区间为：

这表明由莫蒂列夫修正式的引文半衰期计算方法所给出文献半衰期的区间在T1/2∈[3.64-7.93]年，即它可以描述范围是半衰期为3.64-7.93年的学科或专业。

从（11）、（12）和（13）式的计算结果可知，由（6）式给出的文献半衰期的范围要比（5）式和（7）式要大得多，也即（6）式的适用范围要比B-K方程和莫蒂列夫修正式的引文半衰期计算公式要大。

4 结论

我们首次把文献半衰期与普赖斯指数这两个衡量科技文献的老化速度和程度的量度指标联系起来，并给出了这两个量度指标之间的关系式。同时，我们用文献半衰期计算新方法重新计算了文献[5]的数据。计算结果表明，我们可以用该方法直接计算出科技文献的半衰期，且与实际值最为接近。此外，对比（11）、（12）和（13）式的计算结果可知，莫蒂列夫修正式计算的半衰期区间要比B-K方程计算的半衰期区间有所改进，但这2个文献半衰期的计算方法均有局限性，适用的范围在3.47-7.93年。而用文献半衰期计算新方法得到的文献半衰期的区间要比由B-K方程和莫蒂列夫修正式计算的半衰期区间要大得多，它所计算的文献半衰期的范围在1.74-15.2年，这表明文献半衰期计算新方法的应用范围更广，尤其对于某些半衰期较长或半衰期较短的学科或专业适用，比如生物医学的半衰期为3.0年[6]。对于这个学科我们无法用B-K方程和莫蒂列夫修正式的文献半衰期计算方法去研究该学科的文献老化问题。因此，文献半衰期计算新方法对研究科技文献的半衰期和文献老化具有较大的应用价值和学术价值，且比B-K方程和莫蒂列夫修正式的文献半衰期计算方法更具普适性。

[1]Price DS.Little science，bigscience[M].NewYork:Columbia UniversityPress，1963.

[2]Burton R E，Kebler RW.The“half-life”ofsome scientific and technical literatures[J].American Documention，1960，11（1）:18-22.

[3]BrookersBC.The growth，utility，and obsolescence ofscientific periodical literature[J].Journal of Documentation，1970,26（4）:283-294.

[4]Pauline B.The half-life of the chemical literature[J].Journal ofAmerican SocietyInformation Science，1980,31(1):61-63.

[5]丁学东.文献计量学基础[M].北京：北京大学出版社，1993.90-92.

[6]于 光，李洪喜，辛瑞杰.莫蒂列夫文献老化模型的局限性 [J].情报科学，2000，(3):270-271.

[7]陈立新，刘则渊.引文半衰期与普赖斯指数之间的数量关系研究[J].图书情报知识，2007，（1）:25-28.

[8]陈立新，梁立明，刘则渊.力学文献老化速度50年（1954-2003）的变化趋势 [J].现代情报，2006，（10）:12-15，18.

[9]邱均平.文献计量学[M].北京：科学技术文献出版社，1988.97-99.