月亮湖水质评价

2010-05-31孙晓梅曲延光郎振华

东北水利水电 2010年1期

孙晓梅，曲延光，郎振华

（1.吉林省水文水资源局白城分局，吉林白城 137000；2.吉林省水文水资源局，吉林长春 130021）

水质评价方法有两大类，一类是以水质的物理化学参数的实测值为依据的评价方法；另一类是以水生物种群与水质的关系为依据的生物学评价方法。较多采用的是物理化学参数评价方法，其中又分单项参数评价法和多项参数综合评价法。

现以白城地区月亮湖水质监测站的监测数据为例，介绍2种水质评价的方法。月亮湖水质监测站 2008年 3月份监测成果：NH4＋-N 为 0.31mg/L，COD为27.9mg/L，高锰酸盐指数为3.4mg/L，总磷为0.04mg/L，氟化物为0.51mg/L。评价标准采用《地表水环境质量标准》GB3838-2002。

1 单因子评价法

“单因子评价法”，就是用某一参数的实测浓度代表值与水质标准对比，判断水质的优劣或适用程度，参加评价的所有项目只要有1项超标，则断面水质为超标。按单因子评价方法，月亮湖水质类为IV类，见表1。

2 模糊数学评价法

2.1 基本概念

（1）隶属度

以往的水质分级中多用一个简单的数学指标为界限，造成界限两边分为截然不同的等级。例如参数DO，I级水的指标为7mg/L，则 7.1mg/L为水质的污染程度属于模糊概念,所以这里用隶属概念来描述模糊的水质分级界限。所谓隶属度系指某事物所属某种标准的程度。如，DO=7.1mg/L时,隶属 I级水的程度为 100%；6.9mg/L时,隶属I级水的程度达95%。隶属度可用隶属函数表示。为方便起见，取线性函数：

表1 月亮湖水质评价结果

式中 Y—对应于X0或X1所规定的那一级水的隶属度；X—实测值；X0，X1—某项参数相邻的两级水质标准值。

（2）权重及归一化运算

根据各参数超标情况进行加权，超标越多，加权越大。权重值为：

式中 Wi—第i种污染物以平均标准为基准的超标指数，即为权重；Ci—第i种污染物实测浓度；Si—第i种污染物各级标准值的算术平均值。

为进行模糊运算，将各单项权重再进行归一化运算：

模型和建模是生物学核心素养中的“科学思维”的重要形式之一。通过模型构建，能将抽象问题形象化，有助于提升学生“科学思维”能力。模型分为物理模型、数学模型和概念模型。数学模型就是为了某种教学目的,用字母、数字及其他数学符号建立起来的等式或不等式以及图表、图像和框图等描述客观事物的特征及其内在联系的数学结构表达式[1]。在“种群数量变化”一节的教学中，引导学生构建种群数量变化的数学模型，解释种群数量变化规律，并尝试利用这种数学模型解释实际生活中的现象。

式中 Vi—第i种污染物的归一化权重。

（3）模糊矩阵的复合运算

在进行综合评价时,会用到2个模糊矩阵的复合运算。这种运算同一般矩阵乘法相似，不同的是两数相乘“·”改为“∧”，并取其中小者为“积”；两数相加“+”改为“∨”，并取其中大者为“和”。

（4）评价算法描述

设用污水等级标准对T(被评价水质的某个参数)项目进行评价,标准中等级数为 GK，（k=1，2，3，…，s）,即有 s个等级。假设某水质有 m 个评价因素(参数)uj；（j=1，2，3， …，m），每个评价参数有 n 个定性的评价等级 Vi，（i=1，2，3， …，n）。这些等级按评价要求具体划分,可以定为Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，…级别。

对照标准,可以确定某水质的每个评价参数uj所在的评价等级标准，记为Rmn，得到的评价结果如表 2。

表2 评价表

表2反映了各单项参数与等级之间的关系，这种关系用隶属度表示称作模糊关系。表2中Rji表示被评价水质的第j个因素（参数），u可能为等级vi的概率，即隶属度。用模糊矩阵R表示。

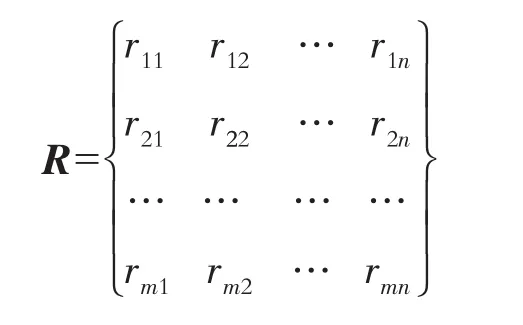
由于评价参数中各个等级标准在某水质评价中的地位不同，由此要求对评价参数赋予权值，其和为 1。用矩阵 A 表示为 A=(a1，a2，…，am)，其中

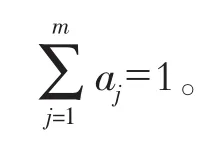
B矩阵表示水质中的某评价中属于V1等级的程度（比例）是 b1，属于 V1等级的程度是 b2，…，根据矩阵B可以综合评价水质所属的等级。

2.2 模糊数学法评价

采用模糊数学法对月亮湖监测站成果进行评价，评价结果见表3。

（1）用隶属度刻划水质分级界限

以COD为例，监测值X=27.9，其相邻地两级水质标准值 X0=20（III级），X1=30（IV 级）。对Ⅲ级水的隶属度为：YⅢ=(30-27.9)/(30-20)=0.21；对Ⅳ级水的隶属度为：YⅡ=(27.9-20)/(30-20)=0.79。即有21%可能划为III级水，79%可能划为IV级水。很明显，就COD这单项污染物而言，该水质不可能划为Ⅰ,Ⅱ,Ⅴ级，故它们的隶属度为零。同样可得砷（As）和铬（Cr）对各等级水的隶属度，并构成m·n＝3×5的模糊矩阵 R。