水平地震力作用下浅埋偏压隧道松动围岩压力的研究

杨小礼，黄波，王作伟

(中南大学 土木建筑学院，湖南 长沙，410075)

与地面建筑物相比，隧道与地下结构本身会受到周围岩土体的约束作用，这就使得隧道结构比地面建筑物有更好的抗震性能。长期以来，人们对隧道与地下结构的抗震设计没有足够的重视，从而不能清楚地认识地震作用下隧道的破坏机理。1995年日本发生了阪神大地震，这次地震使得包括地铁车站及其区间隧道结构在内的大量大型地下结构出现了严重的破坏[1]。2004年日本又发生新泻县中越地震，此次地震导致 24座隧道严重被毁，大部分需要重新修复和加固[2]。由此可见，地震力对于隧道结构的影响是不容忽视的。国外在这方面进行了大量的研究，如：Tamura等[3]提出了沉埋隧道地震反应分析的数学模型；Wang[4]指出现场测得的地震波对于浅埋隧道的影响和单纯的面波如瑞利波是有很大区别的；Navarro等[5]利用文献[6]中的温克勒弹性梁的简化模型，使用有限差分的方法推导了隧道内力和弯矩的解析解；Sanchez-Merino等[7]研究了隧道衬砌对于面波在纵向的简单地震响应。国内在这方面倾向于数值模拟研究，如许增会等[8]对地震作用下隧道的围岩稳定性进行了模拟，提出地震横波比纵波更加容易引起围岩较大的拉应力；陈国兴等[9]对地铁隧道的地震反应进行了模拟，提出利用大型震动台来进行试验的可行性。然而，国内隧道的抗震设计一直以来均采用地震系数法[10]，该方法是用来计算隧道结构的变形和内力的，而对于隧道周边围岩的力学性能的计算未提及[11-12]。我国现行的公路隧道设计规范[10]对于隧道衬砌荷载的计算均未考虑地震力的影响。在此，本文作者基于地震系数法的理论，考虑水平地震力对浅埋偏压隧道周边围岩力学性能的影响，推导出水平地震力作用下浅埋偏压隧道松动围岩压力的解析解，对我国现行的隧道设计规范[10]进行了有利的补充。

1 隧道设计规范解

浅埋偏压隧道荷载计算简图如图1所示。公路隧道设计规范(JTG D70—2004)[10]中附录 E以及附录 F对偏压隧道破裂角β′和β、围岩垂直压力 Q以及水平侧压力ie和ie′的计算公式规定如下：

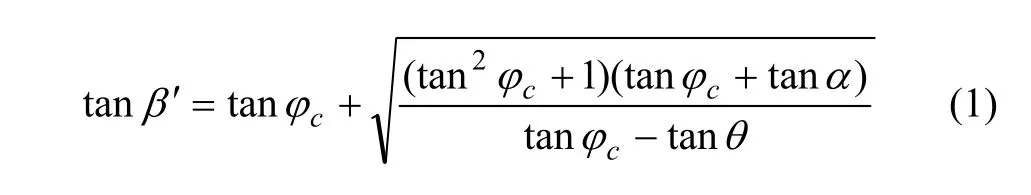
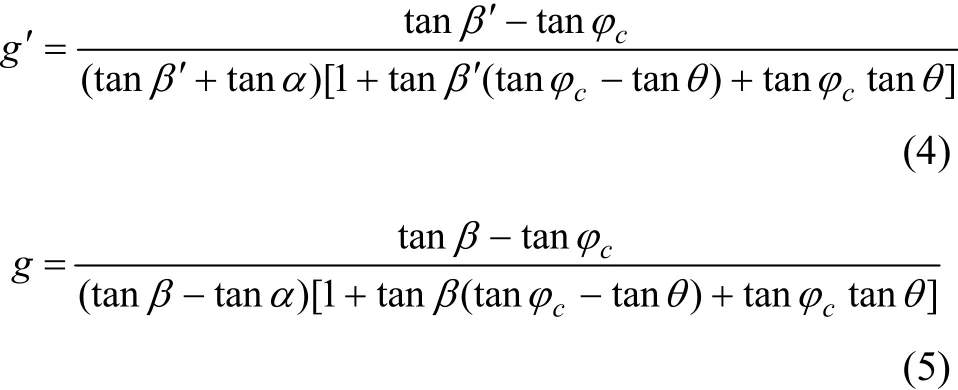
在我国现行公路隧道设计规范(JTG D70—2004)[10]的解析解公式中并未考虑地震力的作用，但是，地震力对于浅埋偏压隧道周边围岩力学性能的影响是不可忽视的。本文在规范[10]的基础上，研究水平地震力对浅埋偏压隧道的影响，并推导出新的解析解计算公式。

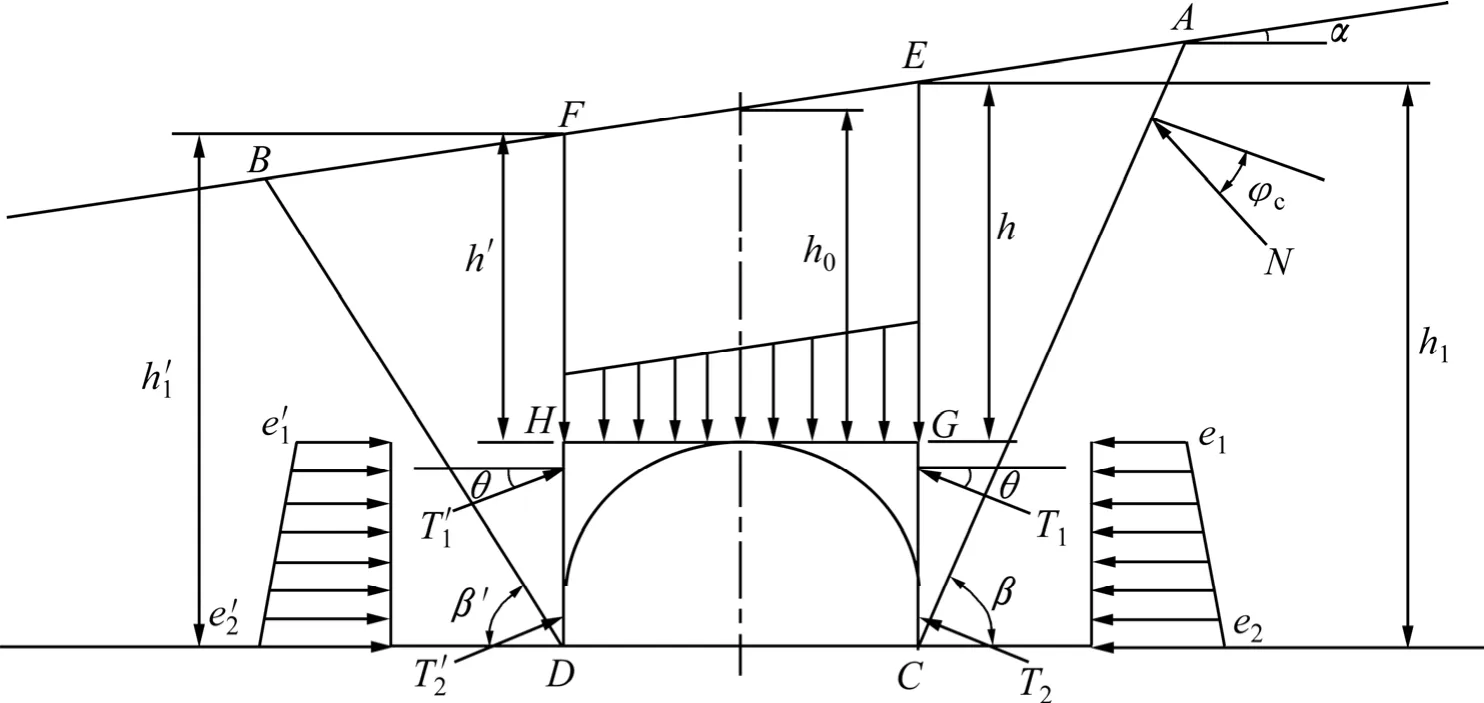
图1 浅埋偏压隧道荷载计算简图Fig.1 Load calculation diagram of shallow bias tunnel

2 考虑水平地震力时偏压隧道衬砌荷载的计算

2.1 基本假定

在现行的公路隧道设计规范中(JTG D70—2004)[10]，考虑到上覆岩体的下沉和位移与很多因素有关，为了方便计算，进行如下假定：

(1) 浅埋隧道埋深大于等效荷载高度且小于等效荷载高度的2.0～2.5倍。

(2) 岩体中形成的破裂面是 1个与水平面成角的斜直面，如图1所示，即面AC和BD。

(3) 当洞顶上的覆盖岩体EFHG下沉时，受到两侧岩体的挟制，而它反过来又带动了两侧三棱岩体的下滑；而当整个岩体 ABDHGC下滑时，又受阻于其周围未扰动岩体。

(4) 斜直面AC和BD是假定破裂滑面，该滑面的抗剪强度决定于滑面的摩擦角以及黏聚力，为了简化计算，采用岩体的计算摩擦角。洞顶岩体EFHG与两侧三棱体之间的摩擦角不同，因为EG和FH面上并没有发生破裂面，所以，可以参考文献[10]中的相关数据进行计算。

本文在上述假定的基础上，对于浅埋偏压隧道，考虑水平地震力的影响，并且按照不利于围岩受力为原则选取水平地震力的作用方向。考虑到地震的不同等级，研究4种不同地震力的作用情况。

2.2 滑动面BD的破裂角

取三棱体BFD作为隔离体进行受力分析，计算简图见图2。从图2可知：作用在其上的力有三棱体BFD的重力 G1、隧道与上覆岩体下沉而带动三棱体 BFD下滑时在FD面上产生的带动下滑力T′以及BD面上的摩擦阻力为N′和水平地震力kG1，这里考虑水平地震力等于重力的k倍。

根据图2，由力的平衡理论可得：

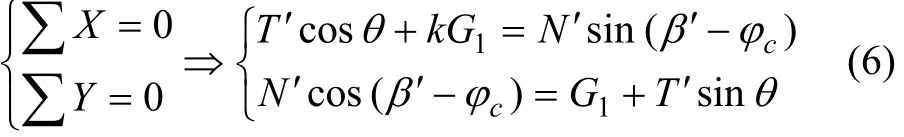
由式(6)，可推导出：

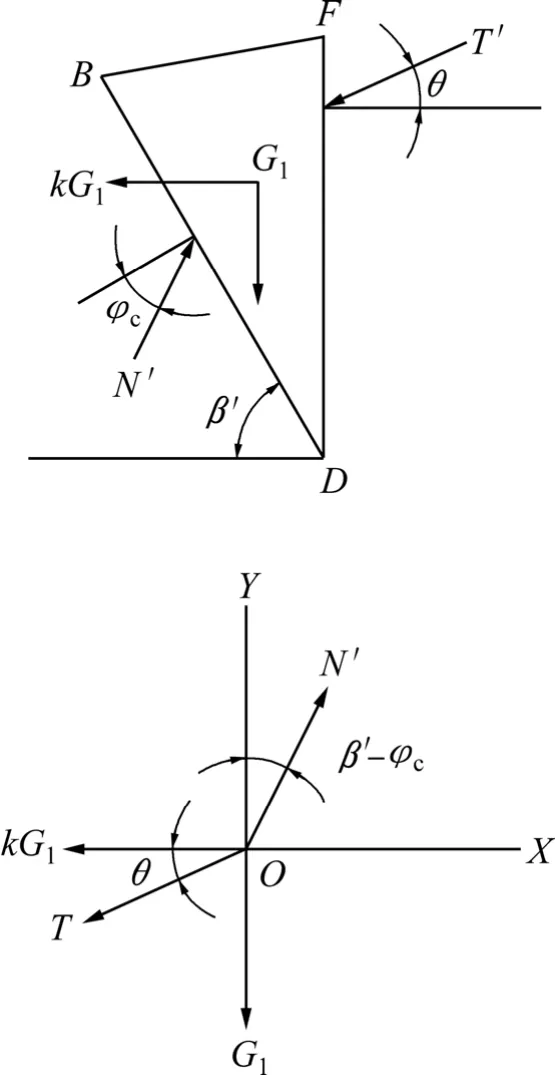
图2 三棱体BFD的计算简图Fig.2 Calculation diagram of triangular prism BFD

围岩的容重为γ，则三棱体BFD的重力为：

由式(10)可知：λ′为 β′，φc和 θ的函数。φc和 θ 为已知，β′为滑动面和隧道底部水平面之间的夹角，而滑动面并非极限状态下的自然破裂角，它是假定与岩体下滑带动力有关的，其最可能的滑动面位置必然是T′为最大值时带动两侧岩体的位置，为此，应利用求极值的方法来求得β′。

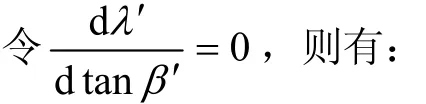
2.3 滑动面AC的破裂角解

取三棱体ACE作为隔离体进行受力分析，其计算简图见图3。从图3可知：作用在其上的力有三棱体ACE的重力 G2、隧道与上覆岩体下沉而带动三棱体ACE下滑时在AC面上产生的带动下滑力T、AC面上的摩擦阻力N和水平地震力kG2。

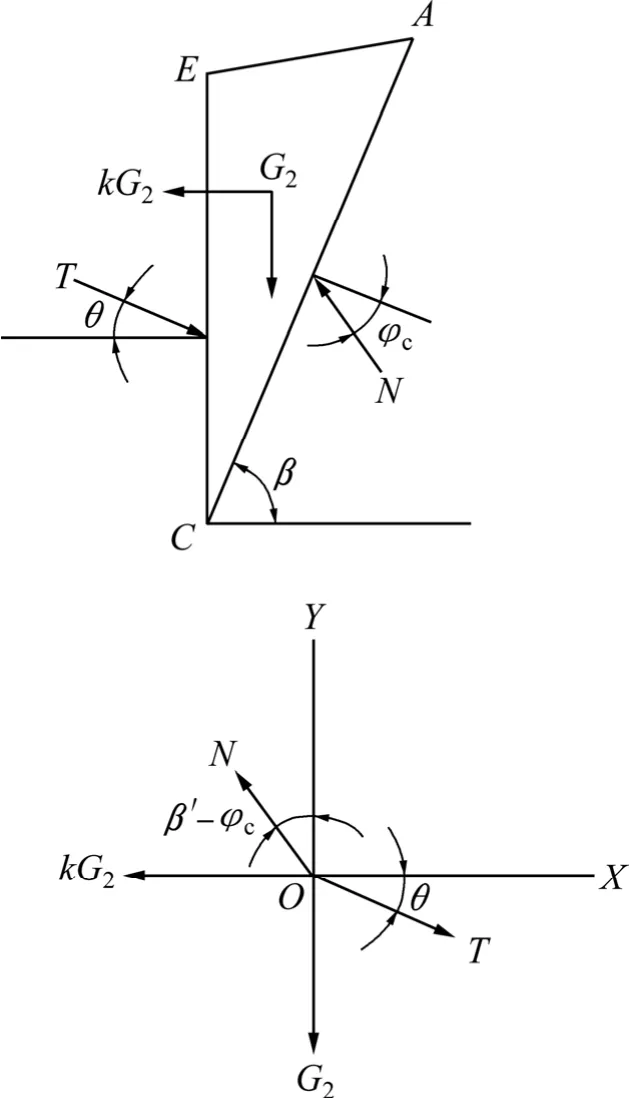
图3 三棱体ACE的计算简图Fig.3 Calculation diagram of triangular prism ACE

根据图3，由力的平衡理论可得：

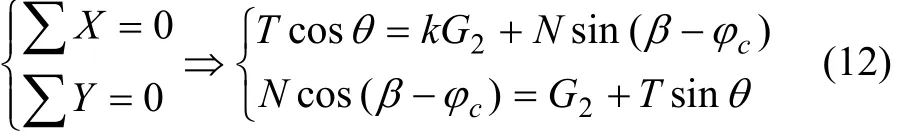
由(12)式，可推导出：

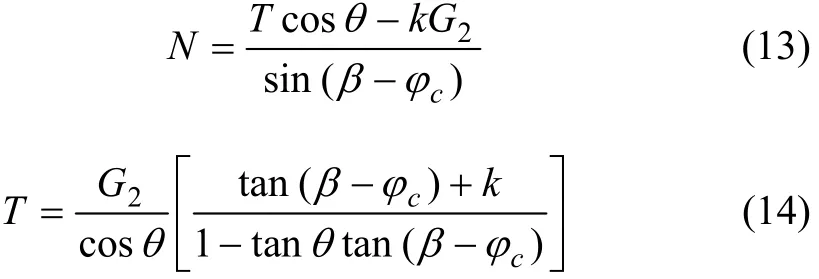
围岩的容重为γ，则三棱体ACE的重力为：

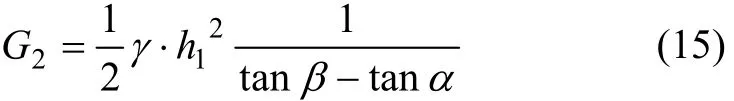
将式(15)代入式(14)，化简得：

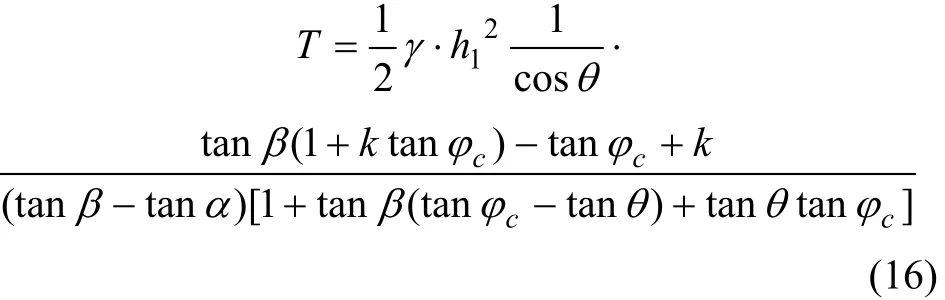
令

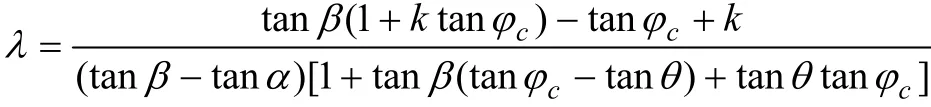
则式(16)简化得：

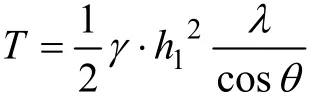
由上式可知，λ为β，φc和θ的函数。φc和θ为已知，β为滑动面和隧道底部水平面之间的夹角，而并非极限状态下的自然破裂角，它是假定与岩体下滑带动力有关的，其最可能的滑动面位置必然是T为最大值时带动两侧岩体的位置，为此，应当利用求极值来求得β。

2.4 围岩垂直松动压力的解析解

取隧道洞顶岩体 EFHG作为隔离体进行受力分析，计算简图见图4。由图4可知：作用在其上的力有岩体EFHG的重力G、三棱体ACE和BFD对岩体EFHG的挟持力T1和1T′、作用在隧道支护结构上的围岩松动压力P和水平地震力kG。

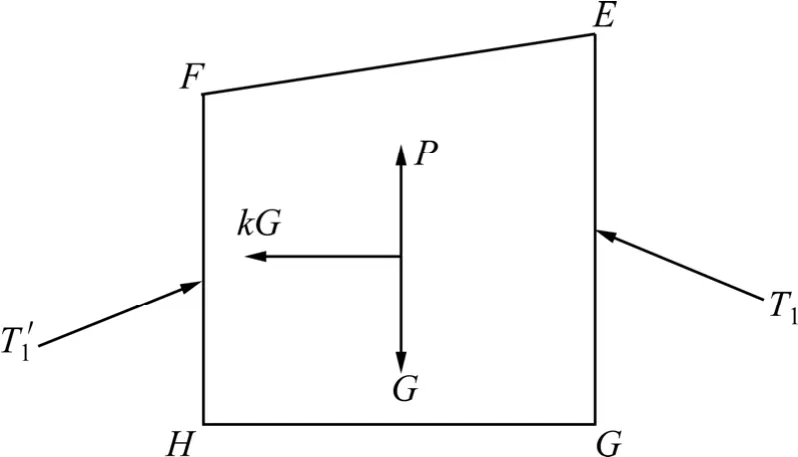
图4 四棱体EFHG的计算简图Fig.4 Calculation diagram of quadrangular prism EFHG

根据图4，从散体极限平衡理论可知：T′为左侧滑动面上的带动下滑力，为1T′和2T′之和；而λ′为滑动面上的侧压力系数。衬砌上覆岩体下沉时受到的两侧摩阻力为1T′，

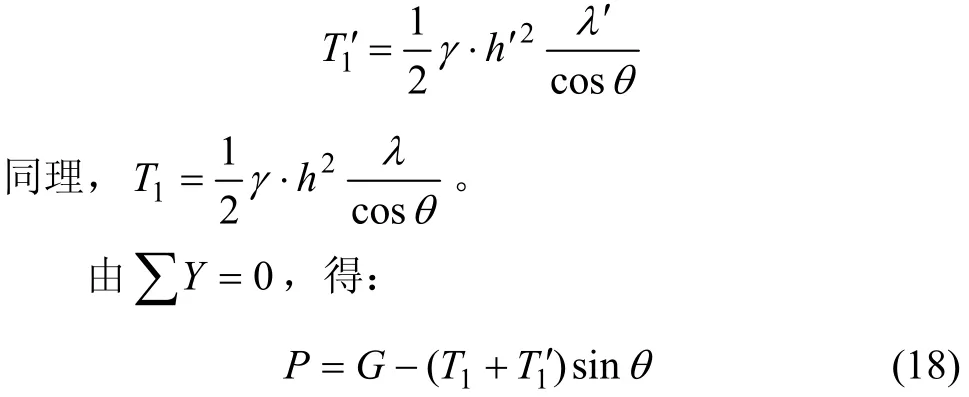
根据文献[10]，假定偏压分布图形与底面坡度一致，隧道宽度为 B，所讨论点的围岩垂直压力为qi，则有：

式中：qi为讨论点的围岩垂直压力；hi为所讨论点的隧道洞顶高度；G为纵向每延米隧道洞顶岩体重力；

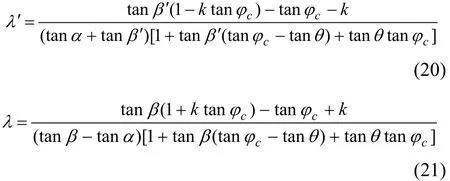
2.5 浅埋偏压隧道水平侧压力的解析解

如图1所示，偏压隧道水平侧压力为：

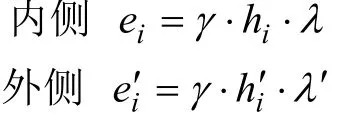
式中：ih和ih′分别为内、外侧任意一点到地面的距离。λ′和λ分别由式(20)和式(21)确定。

3 算例及分析

根据文献[10]，选取不同围岩条件(表1)，并且考虑不同的水平地震力作用，对破裂角进行计算分析，水平地震力取为重力的k倍，k=0.05, 0.10, 0.15, 0.20。

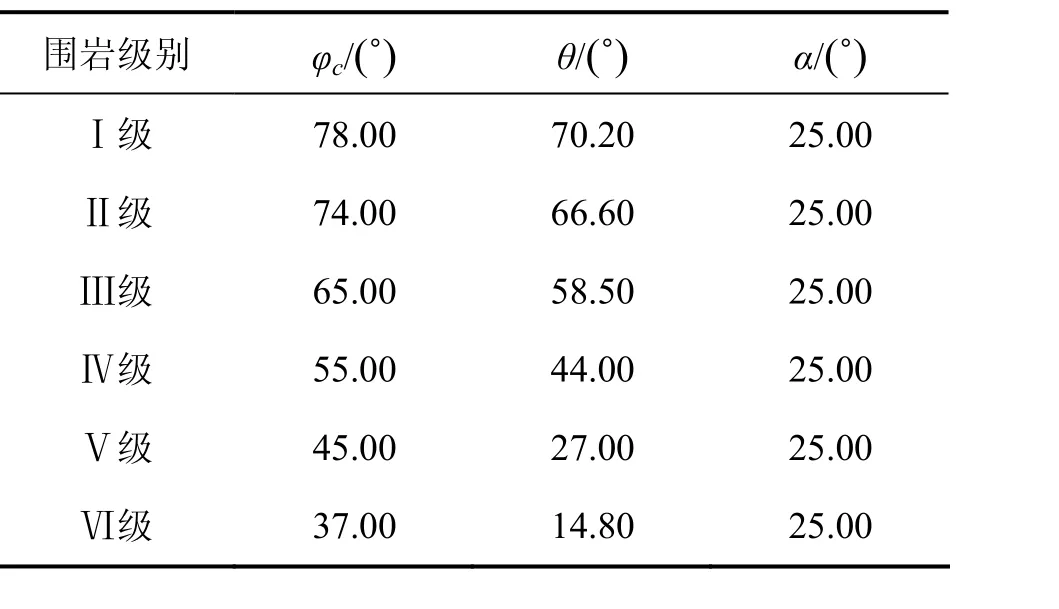
表1 围岩参数Table 1 Surrounding rock parameters

将表 1中的参数代入破裂角计算公式(11)和(17)以及垂直压力公式(19)，所得结果如表2～4所示。

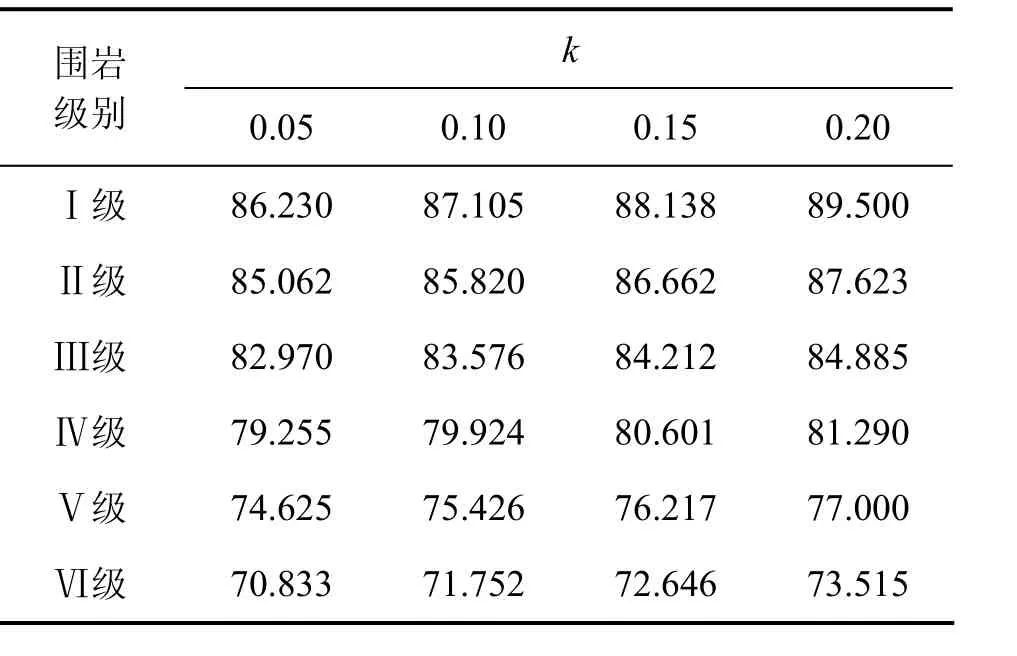
表2 埋深较浅一侧破裂角β′Table 2 Break angle of shallow-buried side of tunnel (°)

从表2可知：当k增大时，从Ⅰ级到Ⅵ级围岩，破裂角β′均呈线性增大，变化率基本相同；而就单独某一个水平地震力来说，随着围岩级别的增大，破裂角β′减小，且变化率增大。

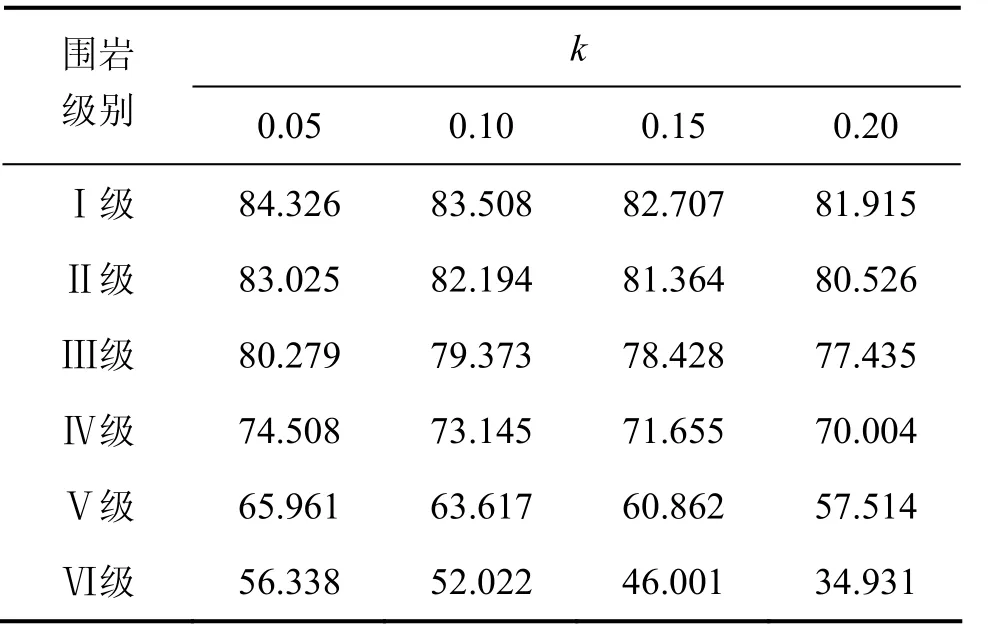
表3 埋深较深一侧破裂角βTable 3 Break angle of deep-buried side of tunnel (°)

从表3可知：当k增大时，从Ⅰ级到Ⅵ级围岩，破裂角β均减小，变化率随着围岩级别的增大而增大；而就单独某一个水平地震力来说，随着围岩级别的增大，破裂角β减小，且变化率增大。

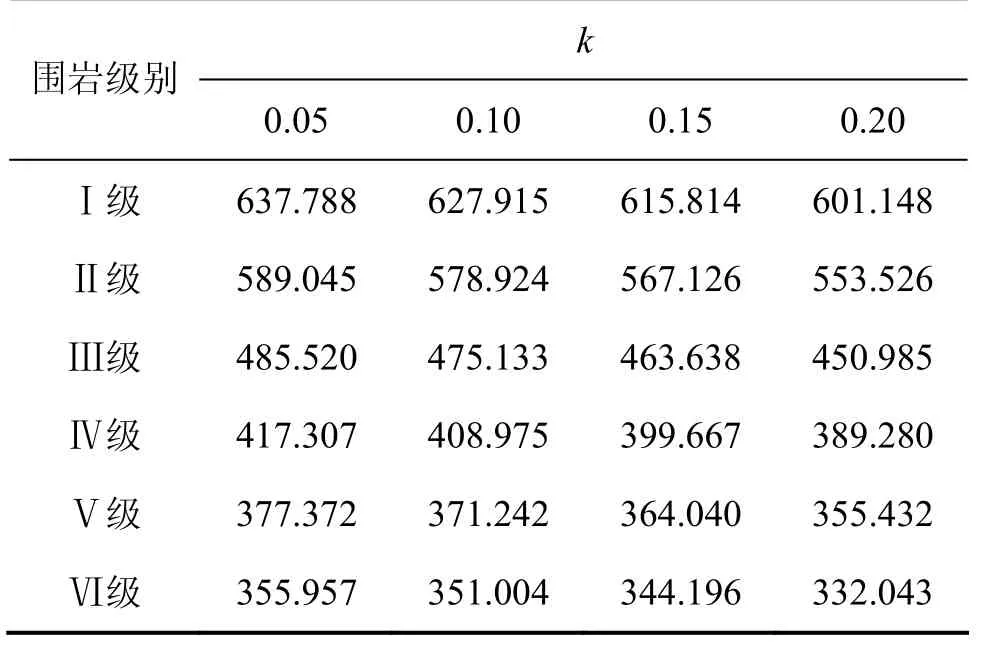
表4 隧道拱顶处垂直压力Table 4 Crown rock pressure of tunnel kPa

从表4可知：当k取不同的值时，隧道拱顶处垂直压力随着围岩级别变化的曲线图形状基本一致，均随着围岩级别的增大而减小；而就单独某一个级别的围岩来说，随着k增大，隧道拱顶处垂直压力减小。

4 结论

(1) 破裂角β′和β都随着围岩级别的增大而减小，且变化率增大。破裂角的变化规律可为地震作用下浅埋隧道地表加固范围提供理论依据。

(2) 水平地震力对破裂角 β′影响很小，而对破裂角β的影响则很明显，特别当围岩变差时，破裂角β的变化很大，如对于Ⅵ级围岩，当k从0.05变化到0.20时，破裂角β减小约22.6°。

(3) 隧道拱顶处垂直压力随着 k的增大而减小，且变化率很小；隧道松动围岩压力随着围岩级别的增大而减小，水平地震力对于隧道松动围岩压力的影响较小。

[1] Hashash Y, Hook J, Schmidt B, et al. Seismic design and analysis of underground structures[J]. Tunneling and Underground Space Technology, 2001, 16: 247-293.

[2] Yashiro K, Kojima Y, Shimizu M. Historical earthquake damage to tunnels in Japan and case studies of railway tunnels in the 2004 Niigataken-Chuetsu earthquake[J]. Quarterly Report of Railway Technical Research Institute, 2007, 48(3): 136-141.

[3] Tamura C, Okamoto S. On earthquake resistant design of a submerged tunnel[C]//International Symposium on Earthquake Structure Engineering. St Louis, Missouri, 1976: 549-554.

[4] Wang J. Seismic design of tunnels: a simple state-of-the-art design approach[R]. New York: Monograph 7 Parsons Brinckerhoff Quade & Douglas Inc, 1993: 15-25.

[5] Navarro C, Samartn A. Simplified longitudinal seismic analysis of buried tunnels[J]. Software Eng Workstations, 1988, 4(1):3-10.

[6] Constantopoulos I V, Motherwel J T, Hall J R. Dynamic analysis of tunnels[C]//Proceedings of the Third International Conference in Geomechanics. Aachen, 1979: 262-265.

[7] Sanchez-Merino A L, Fernandez-Saez J, Navarro C. Simplified longitudinal seismic response of tunnels linings subjected to surface waves[J]. Soil Dynamics and Earthquake Engineering,2009, 29(3): 579-582.

[8] 许增会, 宋宏伟, 赵坚. 地震对隧道围岩稳定性影响的数值模拟分析[J]. 中国矿业大学学报, 2004, 33(1): 41-44.XU Zeng-hui, SONG Hong-wei, ZHAO Jian. Numerical analysis of stability of tunnel surrounding rocks under earthquake[J].Journal of China University of Mining & Technology, 2004,33(1): 41-44.

[9] 陈国兴, 左熹, 庄海洋, 等. 地铁隧道地震反应数值模拟与试验的对比分析[J].自然灾害学报, 2007, 16(6): 81-87.CHEN Guo-xing, ZUO Xi, ZHUANG Hai-yang, et al. Contrast analysis of numerical simulation of subway tunnel earthquake response with test results[J]. Journal of Natural Disasters, 2007,16(6): 81-87.

[10] JTG D70—2004, 公路隧道设计规范[S].JTG D70—2004, Code for design of road tunnel[S].

[11] 杨小礼, 眭志荣. 浅埋小净距偏压隧道施工工序的数值分析[J]. 中南大学学报: 自然科学版, 2007, 38(4): 764-770.YANG Xiao-li, SUI Zhi-rong. Numerical simulation of construction sequence for shallow embedded bias tunnels with small clear distance[J]. Journal of Central South University:Science and Technology, 2007, 38(4): 764-770.

[12] 杨小礼, 李亮, 刘宝琛. 偏压隧道结构稳定性评价的信息优化分析[J]. 岩石力学与工程学报, 2002, 21(4): 484-488.YANG Xiao-li, LI Liang, LIU Bao-chen. Evaluation on structure stability of unsymmetrically loaded tunnels using the theory of information optimization analysis[J]. Chinese Journal of Rock Mechanism and Engineering, 2002, 21(4): 484-488.