改进的遗传神经网络在灰渣粘度预测中的研究及应用*

杨华芬，董德春

(曲靖师范学院 计算机科学与工程学院，云南 曲靖 655011)

煤在气化过程中，仅根据煤灰的熔融特性确定气化工艺是不够的。常用于测定煤灰熔融特性的方法(如角锥法)本身存在较大误差，部分煤灰可能测不到流动温度(FT)特征的温度点。有的灰锥明显缩小甚至完全消失;有的缩小，最后形成一烧结块，保持一定的轮廓;有的灰锥由于表面挥发而明显缩小，但保持原来的形状;SiO2含量高的灰锥容易产生膨胀或鼓泡等，导致测量偏差。通过灰渣粘度的测定可以很好地评价灰渣的流动特性。

煤灰的化学组成比较复杂，其成分对灰渣粘度的影响十分复杂。煤灰粘度的测量成本较高，国外学者开发出很多预测灰渣粘温特性的数学模型，常见的模型有:

(1)Fulcher提出用温度修正因数来保证温度(T)和煤灰粘度(η)的关系［1］:

(2)Reid提出的数学模型如下［2］:

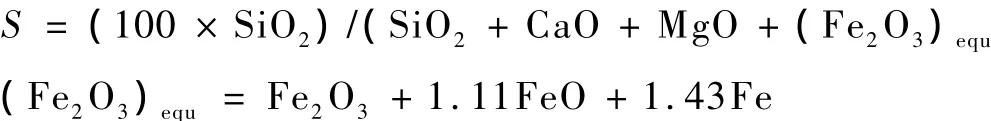
煤灰粘度和温度的关系式:

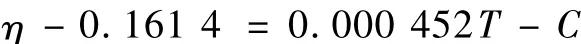
国内外许多学者还总结出一些关于预测灰渣粘度的经验公式［3-4］，常见的有:

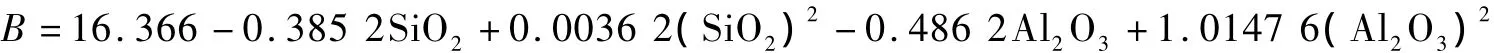
上述模型和经验公式用于预测国内煤种时偏差较大。不同产地的煤，其所含成分不尽相同，化学成分相差较大。通过分析表明:煤灰中含有大量的 Si、Al、Fe、Ca、Mg、K、Na、Ti和 O 元素，并含有 P、B、Cu、Pt、Zn和Mn等微量元素。主要以硅酸盐、氧化物、硫酸盐以及少量的磷酸盐和碳酸盐的形式存在。

神经网络(neural network，NN)以其并行分布处理、自组织、自适应、自学习、具有鲁棒性(Robustness)和容错性等独特的优良性质在模式识别、预测方面等得到广泛应用。应用较为广泛的就是BP网络，但是传统的BP网络学习具有局部极小值以及收敛速度慢等缺点。遗传算法(genetic algorithms，GA)具有较好的全局搜索能力和鲁棒性，将NN和GA结合可以优势互补，但在进化过程中容易出现“早熟收敛”。出现这一现象的根本原因是种群经过进化以后，优胜劣汰，种群的适应度趋同，用这些个体进行遗传操作难以产生优良个体。为改进GA的性能，国内外学者做了大量的研究，提出许多改进算法。文献［5］对适应度进行变换，文献［6］采用自适应的比例选择策略来依据种群性状的改变动态地调整选择压力，文献［7］提出了一种基于实数编码的自适应多亲遗传算法。但对交叉变异概率要随着种群氏适应度的变化而变化以及网络内部存在冗余节点考虑不够。

此处提出一种改进的遗传神经网络并将其用于煤灰粘度预测。首先，根据编码方案将每一个网络进行编码，通过节点的相关性评价，删除网络内冗余的隐节点;其次，统计高于和低于种群平均适应度的个体数目，提出自适应交叉概率(pc)和变异概率(pm)，让pc和pm随着个体适应度的变化而变化，既能开发优良个体又能保证算法收敛。用该算法优化神经网络在一定程度上既能保持种群的多样性，又能防止“早熟收敛”。为验证算法的有效性，将优化后的网络用于灰渣粘度预测。

1 改进的自适应神经网络

1.1 神经网络的基因编码

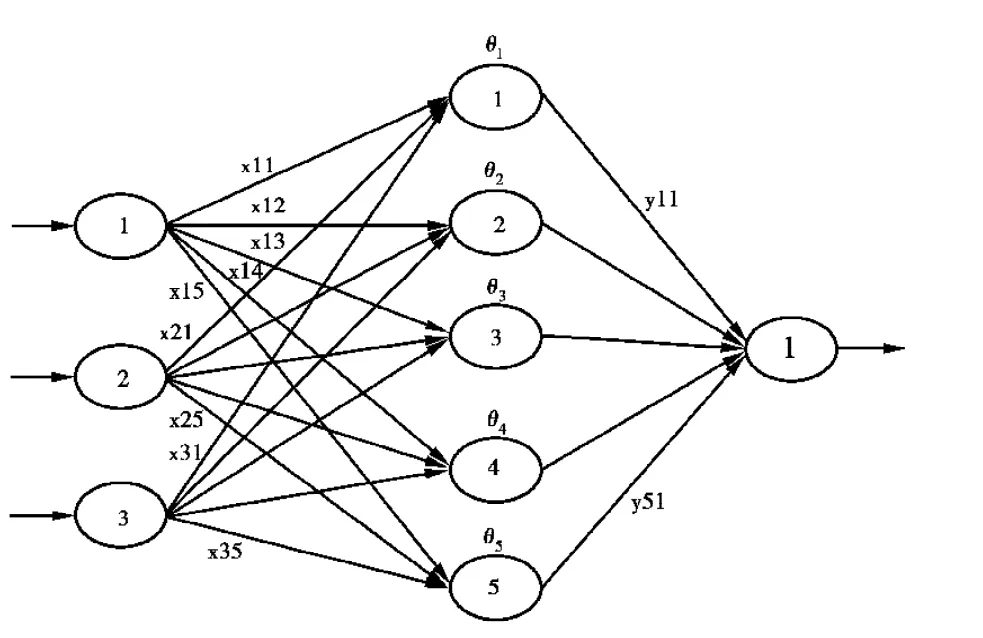
图1 3输入1输出单隐层网络

目前常见的编码有实数编码和二进制编码，若采用二进制编码，会造成编码串太长，且需要再解码为实数，影响网络学习的精度。此处采用实数编码，如图 1 所示的网络，编码为(xij，θj，yjk)，其中 i，j，k 分别为图1所示网络的输入节点数、隐含节点数和输出节点数。图 1所示的编码具体为:(x11，x12，x13，x14，x15;θ1，θ2，θ3，θ4，θ5;y11，y12，y13，y14，y15)=(0.10，0.20，0.30，0.40，0.50;0.60，0.51，0.32，0.33，0.40;0.60，0.34，0.21，0.41，0.70;0.12，0.24，0.30，0.16，0.19;0.30 ，0.50，0.31，-0.40，-0.35)。

1.2 基于相关性评价的隐节点数量确定

神经网络隐节点的个数对网络的性能影响比较大，网络中有一部分隐节点不一定有用，这些无用的节点对求解问题不利。有的学者用公式nh=l确定隐节点个数，其中l为1～10之间的一个整数，n0为输出节点个数，ni为输入节点个数，这并没有什么理论根据。文献［8］把检验样本输入已确定的网络进行检验并比较各模型的预测能力。把实测数据作为输入和输出检验样本带入已建网络模型进行计算，以确定网络模型预报的精度。选取精度最好的网络模型的中间层神经元个数作为所建模型隐节点个数。虽然用该模型预测黄河流域年降水量的精度比较高，但是该建模方法效率比较低，而且难以推广所建模型。针对这些问题，通过评价节点的相关性来确定隐节点的个数，将不相关节点删除。

衡量网络节点的相关性比较困难，可通过评价节点相关性来确定隐节点个数。为确定隐节点i的相关性，先计算存在该节点时网络的性能，然后删除该节点以后再计算网络的性能，节点i的相关性度量方法如下:

1.3 自适应交叉和变异概率

交叉概率pc和变异概率pm等控制参数对系统性能有重要的影响。交叉概率pc的高低决定解群体的更新和搜索速度的快慢，pc太大会使算法的探测能力加强，越容易探测到新的优良个体，增加算法的收敛速度;反之，pc太小会使搜索停滞不前。变异对于保持解群体结构多样性，防止算法“早熟”是一种重要手段。pm太大会使遗传算法变成随机搜索，从而失去其优良特性;pm太小又难以产生新的基因块。因此，合理设定pc和pm的大小对网络优化设计至关重要。

为此，提出一个自适应交叉和变异概率。设第t代种群由个体，，…，构成，适应度分别为，…，，则个体的平均适应度为:

设Ftmax表示最优个体的适应度表示适应度大于的个体平均适应度表示适应度小于的个体平均适应度。x为适应度大于的个体数目，y为适应度小于的个体数目，则pm和pc为:

2 优化设计仿真实验

2.1 设计流程

使用上面提出的设计思想，得到如下的神经网络优化设计流程:

(1)随机生成一定规模的初始种群;

(2)对网络节点进行基因编码;

(3)根据节点相关性评价，确定隐节点的数量，并删除冗余节点;

(4)用自适应交叉变异概率，对种群进行交叉和变异操作;

(5)根据个体的适应度确定下一代种群;

(6)判断进化是否达到最大迭代次数，如果达到则停止，否则转(2)。

该算法考虑冗余节点对算法进化速度的影响，提出基于节点相关性评价的确定隐节点的方法，提高网络学习速度。常用的确定隐节点的方法是通过反复实验或者根据经验确定的。由于初始种群是随机产生的，算法进化速度和寻优能力与初始种群密切相关，隐节点个数随初始种群的变化而变化。通过反复实验确定隐节点数，算法的进化速度和寻优能力带有较大随机性。根据经验确定隐节点个数的方法，并不能针对实际问题调整隐节点个数。由节点相关性确定隐节点个数，可以根据具体问题确定隐节点数目，避免由冗余节点带来不必要的计算。此外提出的自适应交叉变异概率随个体适应度的变化而变化，算法不但能进行局部寻优，而且还可以保持种群的多样性，同时提高算法求精和求泛的能力。

2.2 仿真实验

采用实数编码方法对网络编码，在进行遗传操作时，神经元的输入权和偏置值作为一个整体进行交叉，即任何交叉操作不能通过混合两个节点的内部结构而进行杂交。每一个节点都是一个非线性映射，两个节点的权重组合就会产生一个完全不同的映射，随意组合两个节点的权重的交叉操作更像是一个变异操作。

分别以文献［9］的训练数据和测试数据作为训练样本和测试样本，验证所提出算法的有效性。首先建立4输入1输出单隐层网络，隐节点的初始值为10个。对网络进行实数编码，通过节点相关性确定隐层节点数量，根据式(3)和式(4)得到交叉变异概率。

算法优化神经网络以后的测试结果和文献［9］的测试结果比较如表1所示，种群均值和解的变化如图2所示。从表1可以看出，用提出的算法优化神经网络所得预测结果要比文献［9］的预测结果较好，而且收敛速度比传统遗传算法的速度快，收敛以后较为稳定。用传统遗传算法优化网络时，收敛速度慢，且不稳定。这说明节点相关性评价方法对减少网络冗余节点，提高算法的学习速度确实有效;自适应交叉变异概率同时提高算法求精和求泛的能力。

图2 用传统遗传算法所得种群均值和解的变化

图3 用优化神经网络算法所得种群均值和解的变化

表1 优化神经网络算法的测试结果和文献［9］的测试结果

3 结论

针对传统遗传算法优化神经网络时存在的容易“种群早熟”和后期搜索速度慢等问题，提出了自适应交叉和变异概率，使pc和pm随着个体适应度的变化而变化。难以确定隐节点个数是优化神经网络所面临的一个问题之一。通过节点相关性评价确定隐节点个数，该方法可以随问题的变化而确定相应的隐节点个数，从而加快算法学习速度。

［1］BROWNING G J，BRYANT G W ，LUCAS J A，et al.An Empirical Method for the Prediction of Coal AshSlag Viscosity［J］.Energy and Fuels，2003(17):731-737

［2］REID W T.External Corrosion and Deposita-Boilers and Gas Turbines［M］.New York:Fuel and Energy Science Series，American Elaevier Pubishing Co，1971

［3］孙亦录.煤中矿物质对锅炉的危害［M］.北京:水利电力出版社，1994

［4］任小苟，段盼盼.添加助溶剂降低煤灰熔点及灰粘度的研究［J］.煤化工，1991(2):31-39

［5］KREINOVICH V，QUINTANA C，FUENTES O.Genetic algorithms-what fitness scaling is optimal［J］.Cybernetics and System，1993，24(1):9-26

［6］杨新武，刘椿年.遗传算法中自适应的比例选择策略［J］.计算机工程与应用，2007，43(20):25-27

［7］吴佳英，李平，郑金华.一种自适应多亲遗传算法及其性能分析［J］.系统工程与电子技术，2007，29(8):1381-1384

［8］王利平，刘志强，宗永臣.黄河流域年降水量反算与分析［J］.人民黄河，2007，29(11):36-38

［9］张志文，梁钦锋，王增萤.遗传算法优化 BP网络及其在灰渣粘度预测中的应用［J］.计算机与应用化学，2007，24(5):609-613

［10］黄江波.一种基于自适应遗传算法的统一潮流控制器［J］.重庆理工大学学报:自然科学版，2010，24(03):81-84

［11］赵雪梅.遗传算法及基在TSP问题求角中的应用［J］.四川兵工学报，2009(11):22-27