深市股指波动性的实证研究

段星德，周伟峰

(楚雄师范学院 数学系，云南 楚雄 675000)

股票市场指数收益率波动性的研究是近几年来金融领域的一个重要课题，其研究结论既可作为资产定价、风险度量等的基础，又可给管理者和投资者提供有用的信息。深证指数以所有挂牌的上市公司为样本，其代表性非常广泛，且它与深圳股市的行情同步发布，它是股民和证券从业人员研判深圳股市股票价格变化趋势必不可少的参考依据，深圳证券交易所并存着两个具有代表性的股票指数:一个是深证综指，一个是深证成指。但从运行态势来看，两个指数间的区别越来越明显。深证成指随着每年强势优质股的反复调入，波动率的起点不断前移，逐渐和上证综指趋于同步，深证综指由于不作为，其代表对外首先播报，逐渐被边缘化，但深证综指最近这些年来较少受新股因素的影响，也缺少机构投资者人为炒作的因素，所以较少失真，且众多股市数学模型始终将深证综指作为研究的重要基础。此处的主要目的就是为深证综指和深证成指日收益率的波动性建立合理可靠的模型。

1 模型概述

Bollerslev(1986)把ARCH模型发展为广义自回归条件异方差模型即GARCH模型［1］。GARCH模型的定义如下:如果

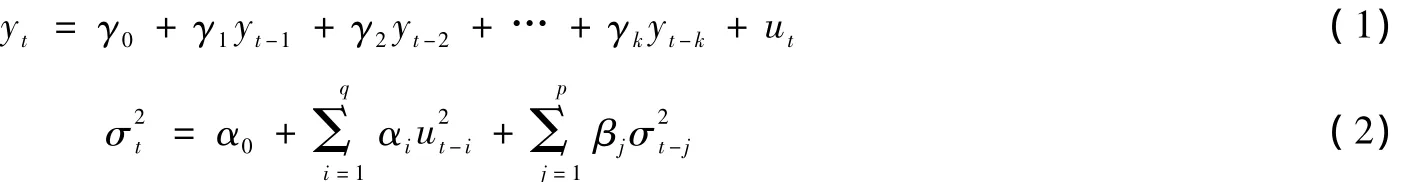
α0＞0，αi≥0，ut=，vt独立同分布;则称序列{ut}服从广义的 ARCH过程，即 GARCH(p，q)过程，记作ut～ GARCH(p，q)(其中ut为误差项，为ut在时刻t的条件方差，此处假定vt服从t分布)。如果满足＜1，则称ut～GARCH(p，q)是稳定过程。

GARCH模型的优点在于解决了ARCH(p)模型中阶数p较大问题，减少了估计量，比ARCH模型具有更高的效益。为了能够刻画“高风险高收益”的经济金融现象，Engle等又提出“GARCH-M模型”。模型定义如下［2］:

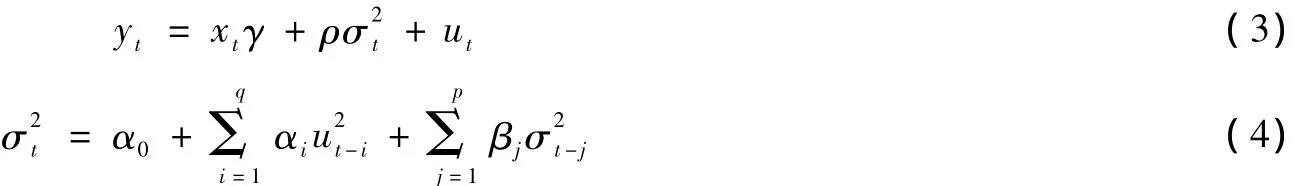
但经典GARCH模型也依然有缺点，比如GARCH模型不能很好的刻画金融市场普遍存在的所谓“杠杆效应”。为了弥补这一缺陷，Zakoian和Nelson又分别提出TGARCH模型和EGARCH模型。

(1)TGARCH模型［3］。TGARCH(Threshold GARCH)模型在经典 GARCH模型的基础上最先由 zakojan(1990)提出，将条件方差定义为:

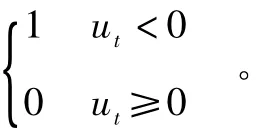
在这个模型中，由于引入dt，股票上涨信息(ut＞0)和下跌信息(ut＜0)对条件方差的作用效果不同。上涨时 =0，其影响可用系数代表，下跌时为+φ。若φ≠0，则说明信息作用是非对称的;如果φ＞0，则表明存在杠杆效应。

(2)EGARCH模型［3］。EGARCH模型，即指数(Exponential)GARCH模型，由 Nelson在1991年提出，模型的条件方差定义为:

模型中条件方差采用了自然对数形式，意味着σ2t非负且杠杆效应是指数型的。式中φi表示杠杆效应系数，若φ≠0，说明信息作用非对称;当φ＜0时，杠杆效应显著。EGARCH模型的优点在于克服了ht非负限制的障碍。

2 实证分析与预测

(1)数据及其统计分析。此处选取的数据是深证综指和深证成指的历史日收盘价格，时间段为2000年1月4日至2007年12月28日，共1 925个。数据均来自大智慧。

在对时间序列数据进行处理时，先对数据取自然对数变换，即Zt=logPt(其中Pt表示日收盘价)，再进行一阶差分后得Rt=logPt-logPt-1，Rt即为这两个股指的日收益率。表1给出了这两个日收益率序列的基本统计。

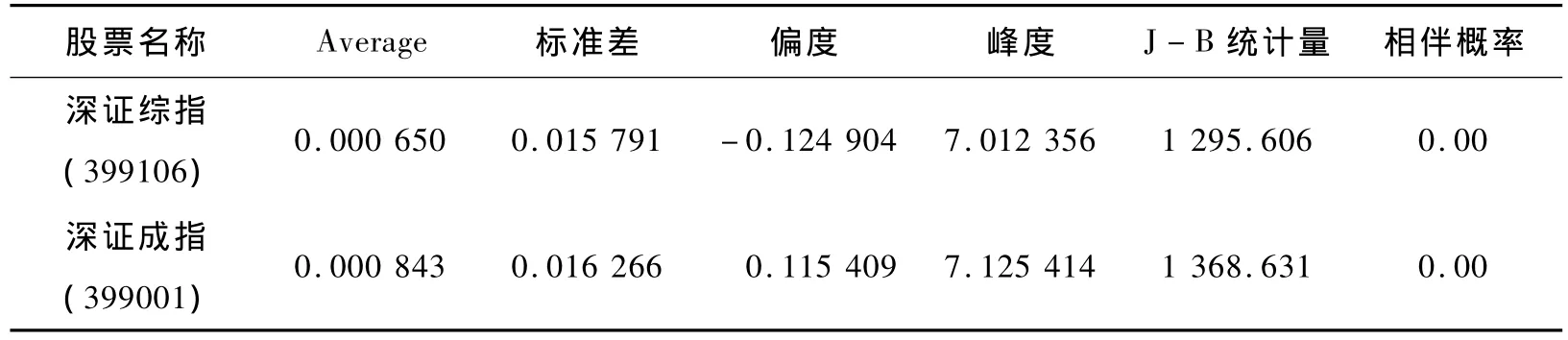
表1 日收益率的基本统计

(2)ARCH效应的检验。序列是否存在ARCH效应，最常用的检验方法是残差平方相关图检验和拉格朗日乘数法(LM)检验。此处采用LM方法首先对深证综指日收益率进行检验。作出深证综指日收益率的折线图。

图1 深证综指日收益率折线图

由图1可知该日收益率序列是平稳的，于是对其作普通最小二乘法(OLS)回归，在5%的显著性水平下，根据回归系数的相伴概率及AIC准则和SC准则，得到回归方程:

括号里的系数是t-统计量的值。这里得到了残差序列，记其为resid01。对resid01进行相关性检验和ARCH效应检验，发现序列resid01不存在自相关性，但存在高阶ARCH(q)效应。故可考虑直接用GARCH类模型进行建模。同理可用R2，t=α0作为均值模型对深证成指进行建模。

(3)建模。通过Eviews6.0软件，可得GARCH(1，1)模型的估计结果。

深证综指日收益率R的均值方程:R1，t=0.048 484R1，t-1+^;Z统计量=(2.082 885)。条件方差方程:

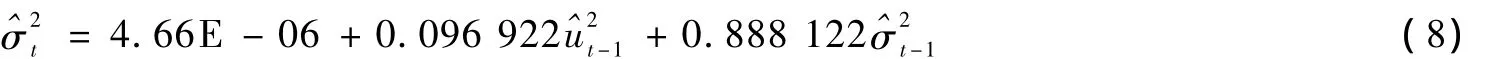
Z统计量 =(3.153 231)(5.995 398)(52.739 59);对数似然L=5 490.281，AIC=-5.7049 20，SC=-5.690 460。

为了进行比较分析，对日收益率R估计GARCH-M模型，通过软件计算可得估计结果。

深证综指日收益率R的均值方程:R1，t=-0.002 919+0.266 748+;Z统计量=(-2.923 258)(3.522 191)。条件方差方程:

Z统计量 =(3.172 648)(5.928 855)(51.24 570);对数似然L=5 498.896，AIC=-5.7098 71，SC=-5.692 526。

以上两类模型的参数估计，均假定模型的随机误差项服从t-分布。由于深证综指日收益率表现出“尖峰后尾”特征，即比正态分布假设具有更厚的“尾巴”，使用t-分布能够比正态分布假设较好地描述日收益率序列的这种厚尾特征，实证表明，这一结论是合理的。运用AIC和SC越小越好的准则，可得出模型(10)比模型(9)更合理。在模型(10)中，日收益率方程包括σt的原因是为了在日收益率的生成过程中融入风险测量，这是许多资产定价理论模型的基础——“均值方程假设”的含义。在这个假设下，ρ应该是正数，结果也正是如此，因此预期较大值的条件标准差与高日收益率相联系，模型(10)中均值方程中的的系数为0.27，表明当市场中的预期风险增加一个百分点时，就会导致日收益率也相应的增加0.27个百分点。估计出的方程的所有系数都很显著，并且系数之和=0.986 148＜1，满足平稳条件，故日收益率的条件方差将收敛到无条件方差=0.000 3321。再对模型(10)估计的残差进行ARCH LM检验，当q=10时，Obs*R-squared的值为5.811 243，相伴概率P值为0.830 9，因此在5%的显著性水平下，可以接受“残差不存在ARCH效应”。

通过相同的建模思想和方法，可对深证成指日收益率R2，t建立如下模型:

深证成指日收益率R的均值方程:R2，t=-0.003 957+0.311 633;Z统计量=(-3.493 889)(3.803 540)。条件方差方程:

Z统计量=(3.339 842)(5.917 820)(52.46 982);对数似然L=5 442.891，AIC=-5.651 654，SC=-5.634 308。

进一步考虑到日收益率波动非对称的情况，引入TGARCH和EGARCH模型，通过实证表明，深证综指日收益率的波动存在“杠杆效应”，而深证成指日收益率的波动的“杠杆效应”不显著，故只对前者进行建模。通过软件，可得两类模型TGARCH(1，1)和EGARCH(1，1)的参数估计结果。从结果中发现:两类模型均能说明股指价格的波动具有“杠杆”效应，但运用相关的准则，认为EGARCH(1，1)模型更合理。如下是模型的参数估计:

深证综指日收益率R的均值方程:R1，t=0.046 469R1，t-1+0.051 089;Z统计量=(2.002 099)(2.427 891)。条件方差方程:

Z统计量 =(-4.806 448)(7.109 642)(-2.082 807)(133.701 7);对数似然L=5 503.483，AIC=-5.716 571，SC=-5.696 325。

在EGARCH模型中，α的估计值为0.203 049，非对称项φ的估计值为-0.029 883。当ut-1＞0时，该信息冲击对条件方差的对数有一个0.173 166倍的冲击;当ut-1＜0，则它给条件方差的对数冲击大小为0.232 932倍。

根据估计出的EGARCH模型的结果，可以绘制出相应的信息曲线。

图2 好消息和坏消息的非对称信息曲线

这里z表示标准化残差或称之为信息，f(z)表示波动性。从图2可以看出，这条曲线在信息冲击小于0时(即z＜0)，比较陡峭，而在正冲击时(z＞0)时比较平缓，从而说明负的冲击比正的冲击对波动性的影响更大，进一步从图形说明存在“杠杆效应”［4］。

(4)基于GARCH类模型的预测。预测时段为2008年1月2日至2008年12月31日，共245个数据。用GARCH-M，TGARCH(1，1)，EGARCH(1，1)模型分别对深证综指日收益率的波动率(方差)进行预测;用GARCH-M模型深证成指日收益率的波动率(方差)进行预测。预测结果如表2。表2给出的是预测值的前5个数据。

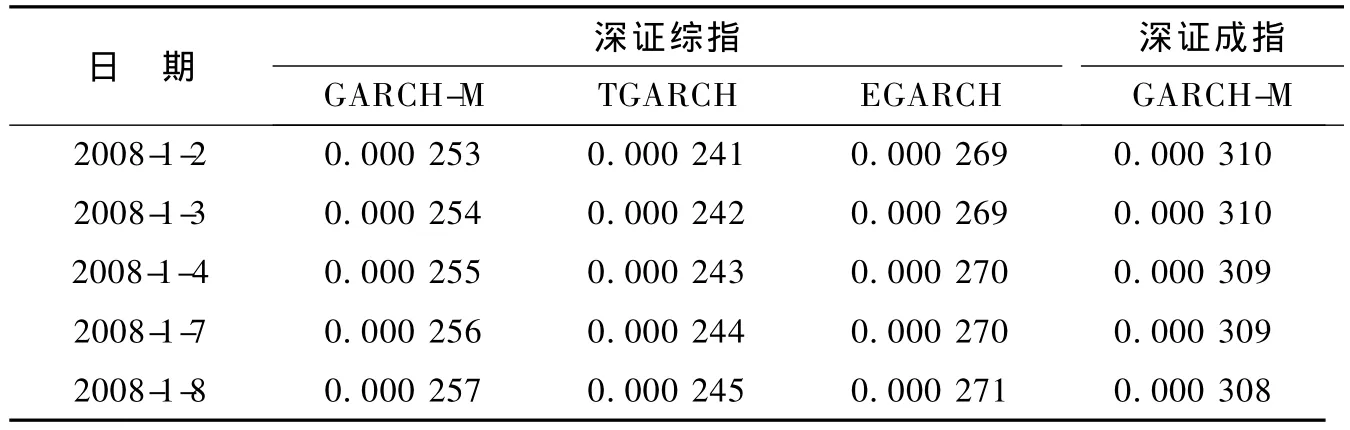
表2 日收益率的波动率预测

从表2可看出，用3类模型分别对深证综指日收益率的波动率进行预测，预测结果均为呈稳定上升趋势，且趋于无条件方差0.000 3321，显然用EGARCH(1，1)模型进行预测效果更佳。而用GARCH-M模型预测深证成指日收益率的波动率，结果表明呈下降趋势，即波动率越来越小。

3 结论

实证研究表明，对于我国股票市场，深市的股指日收益率序列确实存在高峰厚尾性、波动集群性，并用t-分布来描述中国股市日收益率的大涨大跌，符合实际情况。基于t-分布的GARCH-M(1，1)模型能很好的刻画深市股指日收益率的“风险溢价”现象，模型中风险溢价ρ值均为正，表明投资者是风险厌恶的，且ρ值均为0.3左右，表明投资者期望风险求偿约为风险的0.3倍左右。

基于t-分布的TGARCH-M(1，1)和EGARCH-M(1，1)模型的非对称检验表明这个时期深证综指存在显著的“杠杆效应”，而这个时期深证成指的“杠杆效应”不显著，说明深市中这两个不同股指是有差别的，表现出不同的经济现象。所以有人把深证综指和深证成指视为一体，觉得没必要研究深证综指，这一说法是错误的。

［1］BOLLERLEV T.Generalized Autoregressive Conditional Heteroskedasticity［J］.Journal of Econometrics，1986，31:307-327

［2］ENGLE R F，Lilien D M，Robins R P.Estimating time varying risk premia in the term structure:the ARCH-M model［J］.Econometrica，1987，55:391-407

［3］易丹辉.数据分析与Eviews应用［M］.北京:中国人民大学出版社，2008

［4］高铁梅.计量经济分析方法与建模—EViews应用及案例［M］.北京:清华大学出版社，2005