惯性中容忍度及其控制图分析

王传毅

（武汉大学 教育科学学院，武汉 430072）

SPC即统计控制过程，是美国贝尔实验室休哈特博士提出，将正态分布应用于生产管理的质量控制。主要是指应用统计分析技术对生产过程进行适时的监控，科学的区分出生产过程中产品质量的随机波动和异常波动，从而对生产过程中的异常趋势进行预警，以便生产管理人员及时采取措施消除异常，保证生产过程的顺利进行。

SPC借助数理统计的方法对生产过程进行评价根据反馈的信息及时发现系统性因素出现的征兆，采取措施消除其影响，使过程维持在仅存在随机因素影响的受控状态。

但是任何一种检测方法，无论如何先进，都有其局限性。SPC过程在对于随机波动和趋势改变的反应上也有一定的局限性，从而引发虚发警报或未能及时预警。

1 SPC难以探测趋势的一个实例

作者曾在一家加工飞机零件的工厂进行质量检验工作，发现其SPC存在未能及时预警的问题。作者对在一个时间段内有不同工人在同一机床抽取十五个零件的直径数据①数据为：10.027，9.968，9.971，10.026，10.022，9.977，10.021，9.979，10.01，10.009，9.995，10.007，10.007，9.999，10.003；单位是厘米。进行分析。观测值内没有任何超出规定标准的现象，其分布近似与正态分布，也并没有出现几点都在2σ，3σ和中心线同侧，建立极差控制图②在本次抽样观测中，由于只抽取了一个样本，所以用相邻两个样本数据之差的绝对值来代替极差R，RS=|xi-xi+1|，1，2，3...。如下：RS=|xi-xi+1|；i=1，2，3……n+1； 由于 E（R）=d2σx，有 σ=E(RS)/d2=/d2③；所以 d2=3/2.66；带入极差控制图④D3，D4均为与样本量有关的系数。：

没有点出界，过程正常。但是其过程能力指数⑤Cp=(TU-Tl)/，TU,Tl为公差。为0.994，小于正常值1，因此，说明过程中存在着不稳，即有一些小趋势未被探测。

作者对生产线进行检测，发现有以下几个问题：①随着加工时间的增加，砂轮打磨零件所形成的火花会造成工厂新手工人的不适应，导致操纵控制杆的手流汗，眼睛观测度降低，会无意识的加重对于零件的打磨，这会导致大部分加工零件的直径在控制线内略小于规定的标准值；②所在工厂有个不成文的规定此类零件的打磨宜小不宜大。因为零件打磨不够，其直径大于标准值上可通过再加工，将其打磨为合格品，这样有利于节省原材料；③工人具有主观意识性，一方面，当其打磨零件存在一定问题，他会继续保持这种不正确行为，直到意识到这种问题，另一方面，他会在意识到问题时，对其行为进行纠正，并且这种有意思的反思与纠正经常会产生

以上问题的出现可能是同时的，也可能并非同时，同时出现时，可能会互相抵消其趋势的发生，而当某一问题单独出现时，就可能会使过程存在趋势，出现异常。

在日常的生产活动中这种情况几乎处处存在，只是表现严重与否的问题，而在小型的，技术人才匮乏的工厂，现象可能就会普遍一些。当过程发生微小的趋势，由于观测值反应的滞后性而导致不能为SPC所检测。这种情况被一些学者定义为——惯性或信号延迟[1]。

2 容忍度的提出

由上文可知，惯性在SPC中即控制图的观测具有保持原来趋势的状态，会使过程中新趋势的发现滞后。惯性处处存在，关键是看其存在是否对既定的过程造成异常，即在既定的生产精度下使过程发生偏离。也就是说惯性虽无法消除，但其可看作一个适度的量。即多大的惯性可以为SPC所接受，所容忍。惯性越大，其信号延迟越厉害，而惯性越小，其虚发警报的可能性就越大。因此存在一个位置，在虚发警报和信号延迟之间平衡。

虽然在各个领域对于容忍度的定义不大相同，到那我们可以看出容忍度即一种平衡，是既定条件下的一种选择或是次优水平下的一种选择。同时容忍度又是一个适度指标，容忍度过大，说明对于生产者自身的效用压制到较低水平，而容忍度过小，说明对于目标管理尚未达到最优水平。而将容忍度的概念引入SPC，则，容忍度是当过程中存在一定趋势，而白痴当前观测值不发生出界现象所需要的惯性大小。因此用容忍度来衡量惯性大小，对应到生产运作管理中，容忍度越大，说明在一定趋势下过程中的惯性更能保持观测值的不出界，但会增加厂家质量检测和控制的成本，导致成本增高，反之，容忍度越小，惯性越小，其观测值出界也越容易，说明过程存在不稳现象，需要调整。

容忍度的计算需要依靠所依托的控制图的各种数据，不同控制图有不同的计算方法。而本文将选取EWMA控制图作为容忍度计算的载体。EWMA控制图即加权移动平均控制图，其指导思想是基于在加工过程中最近的观测值可以更多反应质量信息的理论，其中新统计变量的权重增大，过去的逐渐减少，能够同时兼顾系统的频域和时域特性。[2]

3 EWM A控制图的建立

在本文中我们只考虑检测过程均值的控制图，我们定义观测值（x1i，x2i，x3i……xni），他们是从正态总体 X 中，以相同的时间间隔取出，每次取n个观测样本。

对每一个样本，我们假定：每一时刻的样本均值X·J

独立同分布（i.i.d）且服从N(μ，σ2)。为在本文中讨论方便我们将观测值进行标准化处理，既 X·i～N(0，1)，休哈特控制图中，CL=0，UCL=L1，LCL=-L1， 当过程均值落在控制线±L1外，（L1》0）被判为出界或失控，EWMA 控制图中，Yi=λX¯·i+(1-λ)Yi-1[3]，Y0=0，0＜λ＜1，λ 为平滑系数，决定以前观测值的权重。在本文中，为测量惯性大小的需要，将选择较小的λ。

E(Yi)=λE(X·i)+(1-λ)E(Yi-1)；Yi=λX·i+(1-λ)Yi-1，∴E(Yi-1)=(1-λ)E(Yi-2)；

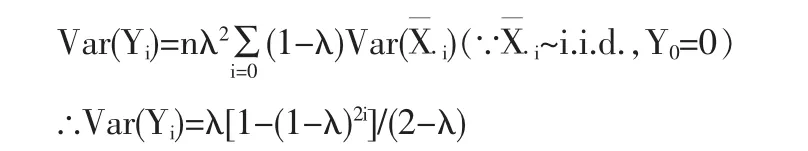
4 EWM A控制图中容忍度的推导

构建统计量——容忍度T，该统计量为下一期观测样本均值偏离目标值却不会使控制图的统计量发出失控信号所能允许的最大程度。此统计量越大表明其惯性越大，即发现这种潜在危险的可能性越小。

（1）出现一个向上趋势而下一统计量不超出控制上限的情况

而当 Yi+1不失控即跑出控制线满足+(1-λ)Yi≤L2

（2）出现一个向下趋势而下一统计量不超出控制下限的情况

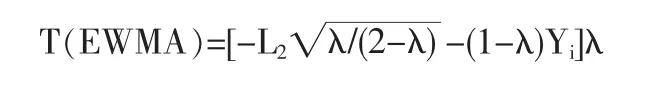
5 EWM A控制图中容忍度数值模拟分析

我们设定ARL=1/0.27即α=0.27因此控制上下线为±3σ，即 L1=L2=3

所以休哈特控制图的上下限为±3，EWMA控制图的上下限为±，（当 λ=0.2 时）且 Yi～N(0，1)

（1）我们产生 1 组 200 个服从 N（0，1）的随机数 X·j，共产生 5000组，计算出（用 EXCEL加载工具宏使用其数据分析功能中产生随机数，并利用其函数功能计算出每组的平均数）

（4）并做出图象如图1。

图中，横坐标表示我们新构建的统计量Yi的取值，由于数据量比较大，并且图比较粗略，我们不能很好的看出Yi在大样本的情况下所服从均值为0，方差为λ(2-λ)的正态分布；纵坐标表示最大容忍度在平滑系数为0.2的时随Yi的变化而变化的不同值。在讨论上限出界和下限出界最大容忍度的大小的实质是一样的，因为如果在稳态的过程中发生向上的趋势，讨论上限出界才有意义，同理，也应该在出现向下趋势的时候，讨论下限出界。

当然在实际情况中，我们并不知道过程发生了何种改变，但是，对域上限出界和下限出界，其容忍度区别在于一个常数，即图中Y轴的截距。为研究方便，本文只选取上限出界的情况进行分析。当我们将一个人为的趋势改变作用于过程中时，随着容忍度的减少，惯性也不断减少，而EWMA控制图中的统计量也不断靠近上界。

图1

6 容忍度的控制图构建

仅仅从容忍度的大小来判断惯性的大小是不够的，因为我们只能从大概的统计量变化的趋势来判断惯性的大小，进而估计潜在的风险大小。因此我们对最大容忍度构件一个控制图，构建过程如下：

∵Var(Yi)=λ/(2-λ)

∴Var[T(EWMA)]=(1-λ)2/λ(2-λ)

所以我们得到T统计量的控制图：

同样的L3的大小也取决于给定ARL的大小。当T跑出上下界时，判为失控。其中心线和上下界大小都取决于λ，所以在操作中应该根据实际情况选取λ的值

由于 Var[T(EWMA)]=(1-λ)2/λ(2-λ)，（0＜λ＜1）对其求导后其导数恒为负，所以T统计量的方差和标准差均随λ的增加而减小 （减小而增大），即控制上下界的距离随λ增加而减小 （减小而增大）。我们通过把不同观测值所对应的EWMA控制图中的容忍度带入容忍度的控制图中，就可以判断其惯性大小是否合理，过程是否处于稳态。

7 结论

采用一般控制图对过程进行监控难免会出现信号延迟的惯性现象，而采用本文中EWMA控制图的惯性及惯性的控制图加以分析，可以将过程中的趋势放大，以此预警，但同时，对于过程的敏感程度增加，也可能会导致虚发警报的产生。在实际的过程监测中，要同时把握信号延迟和虚发警报这两类情况，实际上就是在两类情况中寻造一个平衡点，而作者认为，信号延迟比起虚发警报来，所导致的后果应该更严重。所以，本文中所提出的容忍度及其控制图事实上也是讲二者的平衡点又向虚发警报这类错误进行了小小的迁移。

[1]William H.Woodwall.The Inertial Properties of Quality Control Control Charts[J].Technometrics,2005，47.

[2]Amin.R.W.Wolff.EWMA Control Charts for the Smallest and Largest Observations[J].Journal of Quality Technology，1996，31.

[3]Lucas J.M.EWMA Control Charts:Properties and Enhancement[J].Technometrics，1992，32.