基于实域广义粗糙变量的零售商需求研究

杨 毅，李光金

（1．四川大学 工商管理学院，成都 610064；2．成都纺织高等专科学校，成都 611731）

1 问题的由来

粗糙集与随机集、模糊集有着本质的区别。以一个现实生活中常见的规划问题为例，一个工厂有（x1,x2,…xn）个输入变量，（y1,y2,…ym）个输出变量，我们很容易定义xi或yj是随机变量、或模糊变量，但却不好定义它们是粗糙变量。现有的文献一般不说一个输入（或输出）变量是一个粗糙变量，而是说某个问题可以用粗糙集的方法来处理[1]～[3]。在文献[4]～[6]中，则是简单的将某些参数直接定义为粗糙变量，将它强行构造成粗糙集的结构，形成一大一小两个区间，大区间包含小区间，大区间为粗糙变量的上近似，小区间为粗糙变量的下近似。而文中并未解释这些参数为什么是粗糙变量。本文认为，这种解释只是人为地将此变量做得与粗糙集的结构一样，而没有真正理解粗糙集在解决不确定问题中的意义。当这些粗糙变量的由来语焉不详的时候，相应的粗糙规划模型并不比随机规划或模糊规划更能提供帮助，很难对解决实际问题带来实质的帮助。

例1[5]：

假设共有I个零售商，零售商采用Newsboy模型来订货，生产厂家生产产品需要J种原材料，市场对零售商的需求满足粗糙变量ξ1，ξ2，…，ξI,第i个售货商订货的数量为ai。并假设商品的商场价格固定，生产商根据市场价格制定批发价格，生产厂家接到订单以后根据订单进行生产，产品有一个最迟的交货时间，生产完成后就可以交货。在生产过程中需要储存原材料，原材料j的存储采用Mj循环策略；每Mj天订货，j=1,2,…,J。原材料的运输时间为零，零售商没有卖出的商品，生产商以较低的价格回收，并且假定在储存的过程中，原材料和成品都不会变质。

文献[5]提到，ξ1，ξ2，…，ξI的取值如下：

?

例中的粗糙变量由两个区间数组成，已实现粗糙变量的数学要求，但在现实中，此粗糙变量有什么实际意义呢？它又是如何得到的？此时粗糙规划建立关健在如何理解“市场对零售商的需求满足粗糙变量 ξ1，ξ2，…，ξIi”，而论文中偏偏没有对此进行解释，这个粗糙变量就有了人为构造之嫌。

2 理论背景

2.1 Pawlak粗糙集

首先对粗糙集进行定义。

定义1[7]粗糙集理论中的不确定性和模糊性是一种基于边界的概念，即一个模糊的概念具有模糊的边界，每一个不确定概念由一对称为上近似和下近似的精确概念来表示：设给定知识库K=(U,R),对于每个子集XU和一个等价关系Rind(K),可以根据R的基本集合来划分集合X:

R_(X)=∪{Y∈U/R:Y⊆X}

R-(X)=∪{Y∈U/R:Y∩X≠φ}

BNR(X)=R-(X)-R_(X)

式中，R_(X)和R-(X)分别称为X的R下近似和R上近似，BNR(X)称为X的边界。集合的下近似是包含给定集合中所有基本集的集合,集合的上近似是包含给定集合元素中所有基本集的最小集合。显然,当BNR(X)≠0时,X为粗糙集。

定义2[7]具有相同上下近似集的集合被称为粗糙集，用

2.2 实域粗糙集

DEA模型中的输入变量或输出变量一般为连续变量。为解决经典的粗糙集只能处理离散数据的局限，有必要将粗糙集推广到实数域中。

Pawlak在1999年[8]将粗糙集的思想推广到实数域中。

设 R 是实数集，(a，b)是 R 上的开区间，(a，b)上的实数序列 S={x0,x1,…，xn}，使 a=x0＜x1＜…xn=b，则 A=（R，X）称为由 S生成的逼近空间，S称为离散化序列，每个S都在（a,b）上定义了一个划分：π（S）={{x0},{x0,x1},{x1},{x1,x2},{x2},…{xn-1,xn},{xn}}，相当于定义了一个等价关系，于是对于∀x∈(a,b)，其在S下的下逼近和上逼近可定义为：

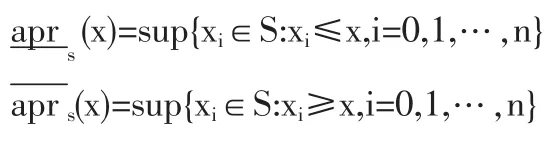
3 本文对实域粗糙变量定义的解释

在实域范围内，粗糙变量的值域有三个可能值，分别对应上近似、下近似和近似精度：

大区间代表上近似，是可能出现的连续实值的最大范围，由实数序列的并构成；

小区间代表下近似，是必然出现的实值范围，由实数序列的交构成；

由于上近似和下近似都是实区间，我们可较方便的定义粗糙变量的粗糙近似精度：

α(x)=|下近似|/|上近似|

以下都以例1中的粗糙变量ξi为例。

3.1 以任意两期的需求量为区间数来构造粗糙变量

假设市场对零售商i的需求为粗糙变量ξi，它由任意两期的需求为实区间[a,c],[b,d]构成，其中a≤b≤c≤d。

从pawlak实域粗糙集定义来看，实域粗糙集的上近似是

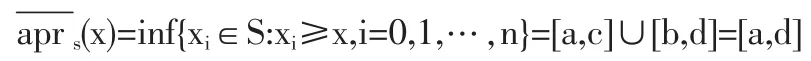
实域粗糙集的下近似是

则ξi=([b,c],[a,d])，实域粗糙集的近似精度是

α(x)=(c-b)/(d-a)

设市场对零售商1的需求为粗糙变量ξ1，它由任意两期的需求为实区间构成，这两个区间的并构成粗糙变量ξ1的上近似，它们的交构成下近似。即ξ1=([200,210],[190,220])。

它的近似精度是

若实际情况为a≤c≤b≤d，即两个实区间交集为空，则实域粗糙集的上近似是

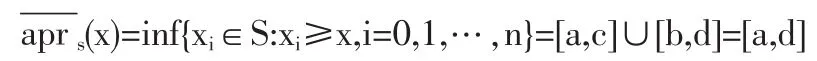
实域粗糙集的下近似是

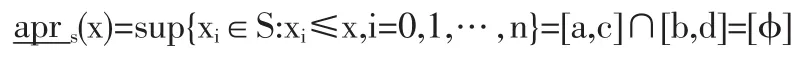
则 ξi=([φ]，[a,d])，仍然满足粗糙集的要求。

设市场对零售商1的需求为粗糙变量ξi，它由任意两期的需求为实区间[190,200],[210,220]构成，这两个区间的并构成粗糙变量ξ1的上近似，它们的交构成下近似。即ξi=([φ]，[190,220])。

3.2 以n期需求量为区间数来构造粗糙变量

假设市场对零售商i的需求为粗糙变量ξi，它由n期的需求为实区间[a1,b1],[a2,b2],…，[an,bn]构成。

则实域粗糙集的上近似是

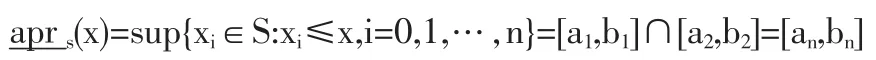
实域粗糙集的下近似是市场对零售商1的需求如下表：

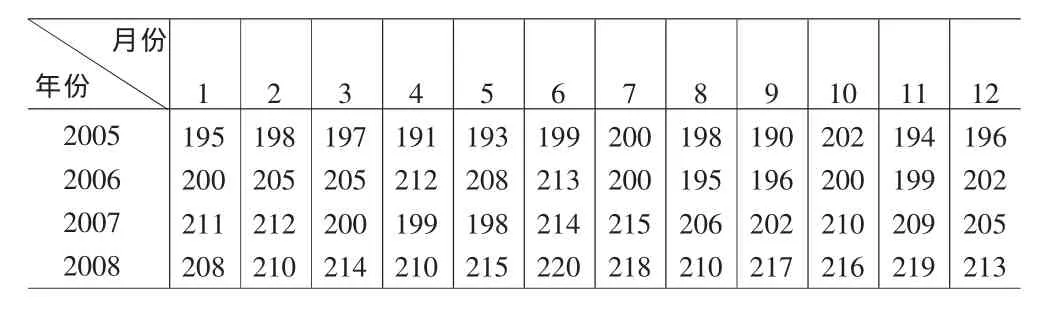
月份年份123456789 2005 2006 2007 2008 195 200 211 208 198 205 212 210 197 205 200 214 191 212 199 210 193 208 198 215 199 213 214 220 200 200 215 218 198 195 206 210 190 196 202 217 10 202 200 210 216 11 194 199 209 219 12 196 202 205 213

可知市场对零售商1的每月需求都是一个区间数，12个月可得12个区间数：

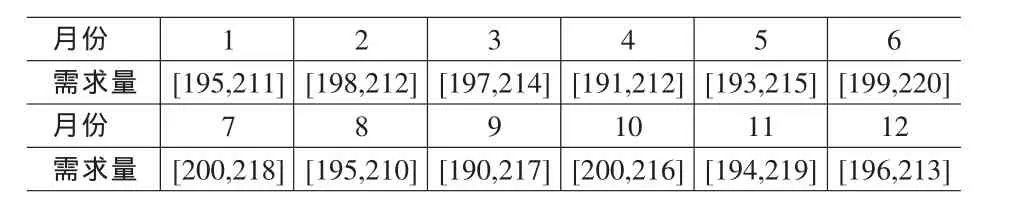
月份需求量月份需求量123456[195,211]7[200,218][198,212]8[195,210][197,214]9[190,217][191,212]10[200,216][193,215]11[194,219][199,220]12[196,213]

从上面的分析可看出，上近似由每月需求量数值的并构成，是需求量的波动范围；而下近似是由每月需求量数值的交构成，是需求量最大可能范围。最大可能范围在波动范围内出现的可能性为0.333。这样，就真正解释了在应用中实域广义粗糙变量的由来和它的意义。

4 粗糙变量的求解

5 结束语

粗糙变量不象随机变量或模糊变量一样在数学规划中得到大量的应用。本文认为现有的文献并未从粗糙集本身的特点去解释粗糙变量的意义，而是简单模仿随机变量或模糊变量，同时在数学上构造一个满足粗糙集形式的变量，得到的结论非常牵强。本文通过对基于实数域的广义粗糙变量的分析，用零售商需求模型对如何得到此粗糙变量给出了一个实例解释。并在此基础上，提出了粗糙变量的求解。实域广义粗糙变量能比区间变量处理更复杂的不确定信息，必然在更多的领域中得到应用。

[1]胡可云,陆玉昌,石纯一.粗糙集理论及其应用进展[J].清华大学学报,2004，（1）.

[2]杨星.粗糙集理论与相关不确定性理论的辨证研究[J].微电子学与计算机,2006，（3）.

[3]漆桂林.粗糙集与模糊集的转化算法分析[J].宜春学院学报,2003，(4).

[4]贾晓秋,刘林忠.粗糙环境下立体运输问题模型与算法[J].兰州交通大学学报(自然科学版),2005,（8）.

[5]刘乐.抽象空间上的粗糙变量及粗糙规划[D].南京理工大学硕士论文.

[6]刘杉,谢辉.基于粗糙理论的高速公路财务评价方法研究[J].统计与信息论坛,2008，（10）.

[7]Pawlak Z．Rough Sets[J].International Journal of Information and Computer Sciences，1982，11(5)．

[8]Pawlak Z．Rough Sets， Rough Function and Rough Calculus[A].Rough-Fuzzy Hybridization：A New Trend in Decision-Making[C]．Singapors：Springer-Verlag，1999．

[9]王緌,徐玖平.一类基于不定性复杂系统的粗糙GMDH模型及实证分析[J].系统工程理论与实践,2004,（7）.