应用于Σ-ΔA/D转换器的数字抽取滤波器的设计

郭来功，欧阳名三，赵泓扬

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

利用超大规模集成电路技术实现高精度的A/D转换器通常采用过采样技术，该技术包括调制器和数字滤波两部分。由于调制器的输出仅仅是对模拟信号的粗略量化，而数字滤波器主要是对调制器的输出进行处理，其处理包括：(1)将基带外的量化噪声进行过滤；(2)由于调制器的输出为输入信号Nyquist率的M倍的数字码流，因此要对其进行M倍的降频，使输出的频率为Nyquist率；(3)将数据码流进行编码，得到与模拟信号对应的数字值。因此数字滤波器是过采样A/D转换器中最大最复杂的器件，同时也决定了A/D转换器面积的大小。

1 抽取滤波器结构分析

从滤波器结构的复杂程度上分析，当采用单级滤波器来实现时，根据FIR滤波器的系数数目正比于滤波器的输入频率fs与过渡带宽Δf的比值的理论[1]，如果用多级滤波器来实现，每一级的fs/Δf都可以得到很大的降低，总的fs/Δf也可以得到降低，同时也减少了滤波器的系数数目，结构变得简单。

从功耗和面积上分析，滤波器的功耗与滤波器的阶数和工作频率成正比，若采用多级实现，阶数和工作频率都将大大降低。一般而言[2]，过采样率在32～128之间时，多级实现的功耗是单级实现功耗的8%～15%。根据以上理论，在实现抽取滤波器时采用多级来实现。本设计中前级调制器的过采样率为32，在抽取滤波时将进行32：1的降频。由于梳状滤波器的阻带很窄，并以 ω=2πk/N为中心周期重复，因此，可以用于多级抽取的第一级滤波器，后级可以采用多个半带滤波器来实现。由于半带滤波器的过渡带过宽，加上梳状滤波器可能会导致通带内幅度下降，故最后一级可以采用一个FIR滤波器进行补偿。抽取滤液器框图如图1所示，x(n)为输入信号按照Nyquist率采样得到的数字系列，y(m)为序列x(n)抽取后得到的新序列。

图1 抽取滤波器框图

2 滤波器设计及仿真

在本设计中，过采样率为32，对多级抽取滤波器来说，主要目的是减少运算量和数据的存储量，这两项都与滤波器的长度有关。长度N是级数和各级抽取率的复杂函数，从N的最小角度出发[3]，选取第一级的梳状滤波器的抽取率为8，后面采用2个半带滤波器分别进行抽取率为2的降频。

由于单级梳状滤波器的传输函数在各区间内只有一个一阶零点，其衰减不足以使ADC实现更高分辨率。这时，最好采用(L+1)级梳状滤波器级联的形式(L为调制器的阶数[4])。本设计中前级调制器阶数为4，所以梳状滤波采用5级串联形式，抽取率M为8。

梳状滤波器后采用两个半带滤波器级联实现4倍抽取，每个半带滤波器抽取率为2，使用凯泽窗法设计。这意味着通带波动 δp与阻带波动 δs相等， 在 ADC为16 bit分辨率的情况下，信噪比 SNR＝98 dB，可以得到两级半带滤波器的阻带波动值为δs=10-AdB/20≈10-100/20=10-5。采用窗函数法的通带波动与阻带波动相等，即通带波动δp=10-5。

2.1 梳状滤波器的设计

梳状滤波器的阶数为5，滤波器的节数等于抽取率M(即 8节)，所以其传递函数为：

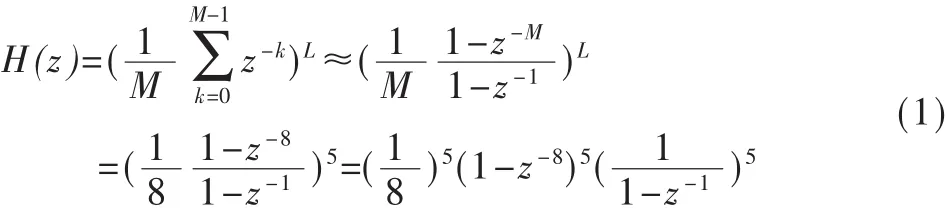
实现梳状滤波器有多种方式，本设计采用图2所示的开关降频方式来实现[5]。因为其差分操作是在较低频率下实现，功耗较低；频率抽取在积分器之后、差分器之前进行，减少了所需要的存储单元。

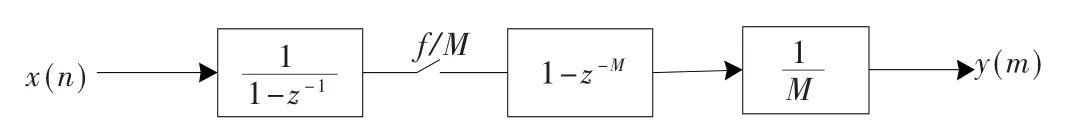
图2 开关降频方式实现梳状滤波器

5阶的梳状滤波器可以采用流水线级联形式来实现，图3为3阶梳状滤波器的结构图。5阶的框图可以以此类推来实现。

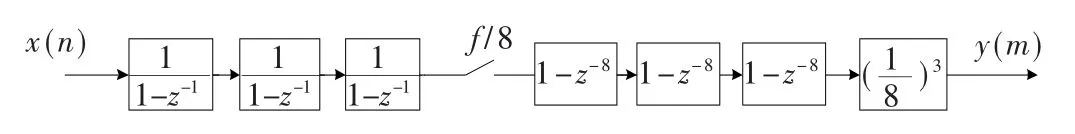
图3 3阶梳状滤波器级联结构图

对于滤波器的字长选择，理论上字长越长越好，但是字长的增加意味着运算量的增大，特别在硬件实现时，将增加电路的复杂度。由滤波器的频率响应可以看出，不计算归一化因子，滤波器的系数全部为正整数。若调制器输出Bi为1 bit码流，则梳状滤波器的字长可以用 式 (2)来 确 定[6]：

梳状滤波器的寄存器字长为16 bit，对滤波器的位数进行截断，最终的输出可以确定为13 bit。

经过梳状滤波器滤波后，输出噪声的频谱密度为：

式中，T为抽样间隔，σe为量化噪声的均方根值，f为数字信号频率。输出信号的噪声功率为：由式(1)得到的梳状滤波器的幅频特性如图4所示。

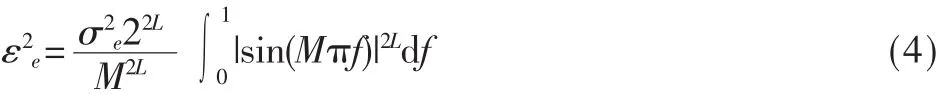
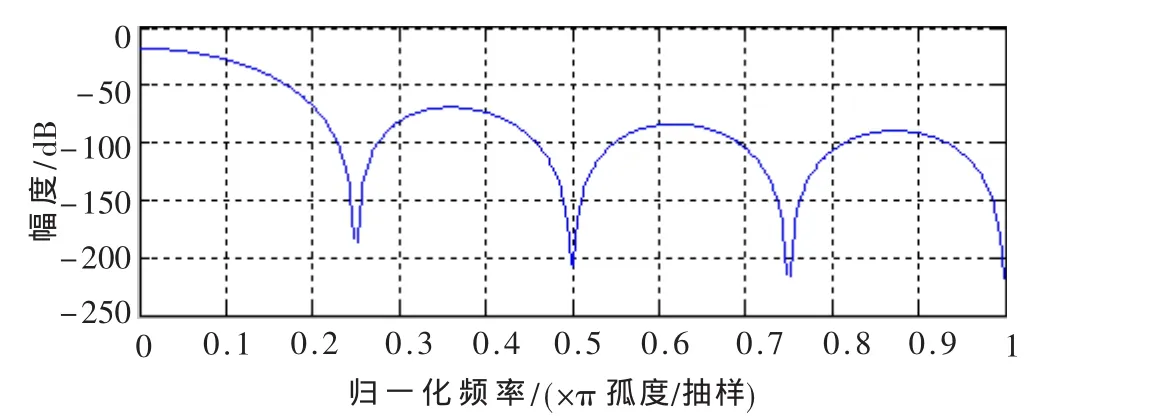
图4 梳状滤波器幅频响应

2.2 半带滤波器的设计及仿真

半带滤波器是一种特殊的FIR低通滤波器，本设计采用多相结构来实现[7]，如图5所示。输入开关把输入奇、偶序列的数据分别送到奇、偶两条支路；输出在两条支路分别输入一个新的数值后才产生一个值，这样可以使采样率减半，而且滤波器一半的系数为零，计算的复杂度又降低近一半，同时系统的冲激响应对称，这就大大降低了实现的复杂程度。

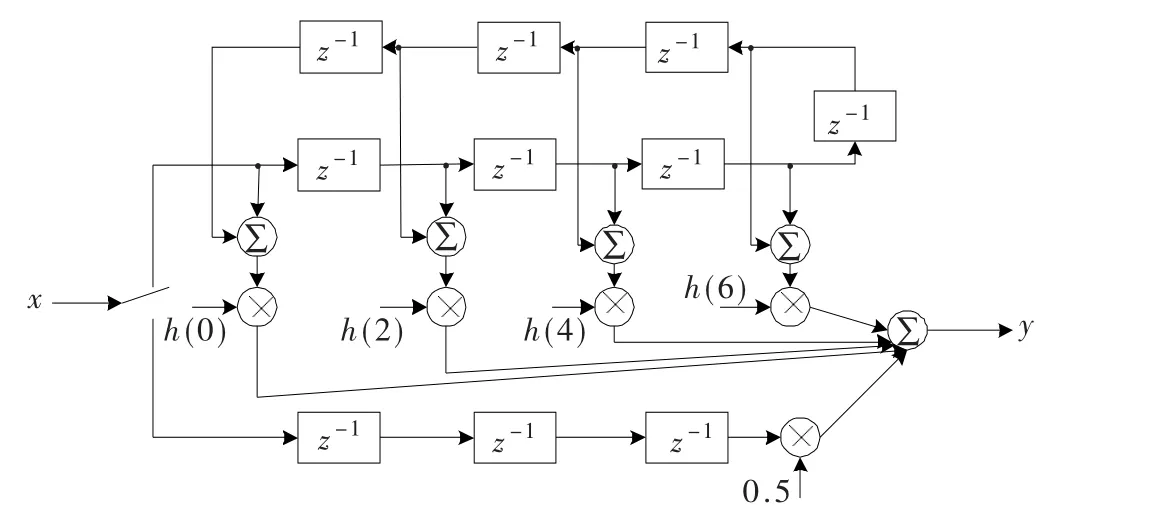
图5 半带滤波器的实现结构

本设计采用窗函数法(凯泽窗法[8])设计。为了得到滤波器所需阶数L，首先要计算过渡带宽 Δf。根据半带滤波器的特性：

式中，ωs、ωp分别为阻带边频和通带边频， 设 ωp＝α×2π，则：

式中，α=fp/fm为通带宽度确定的比例系数，其中，fp是半带滤波器的通带宽度，fm是半带滤波器的输入采样频率。

第一级半带滤波器的通带宽度为ωp=π/8，过渡带宽为Δf=3/4，得到半带滤波器的阶数L：

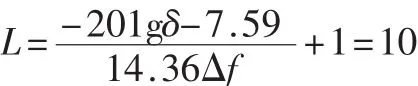
凯泽窗函数参数β可以确定为：

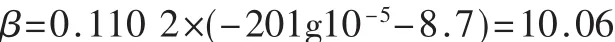
同样地可以设计第二级的半带滤波器。图6给出了第一级、第二级半带滤波器的幅频特性图。

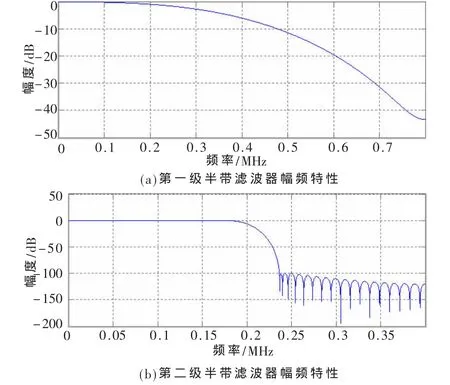
图6 两级半带滤波器幅频特性

两级半带滤波的系数分别如表1、表2所示。

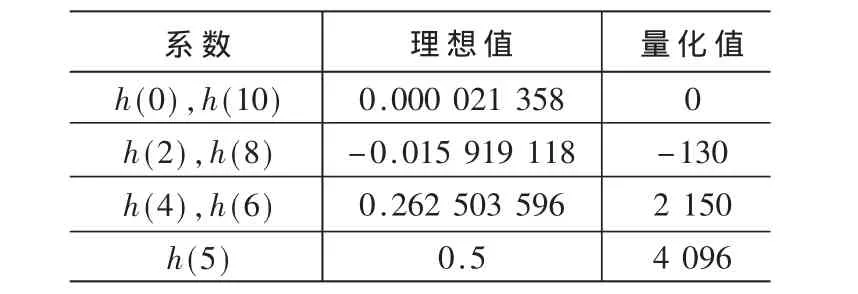
表1 半带滤波器1的系数

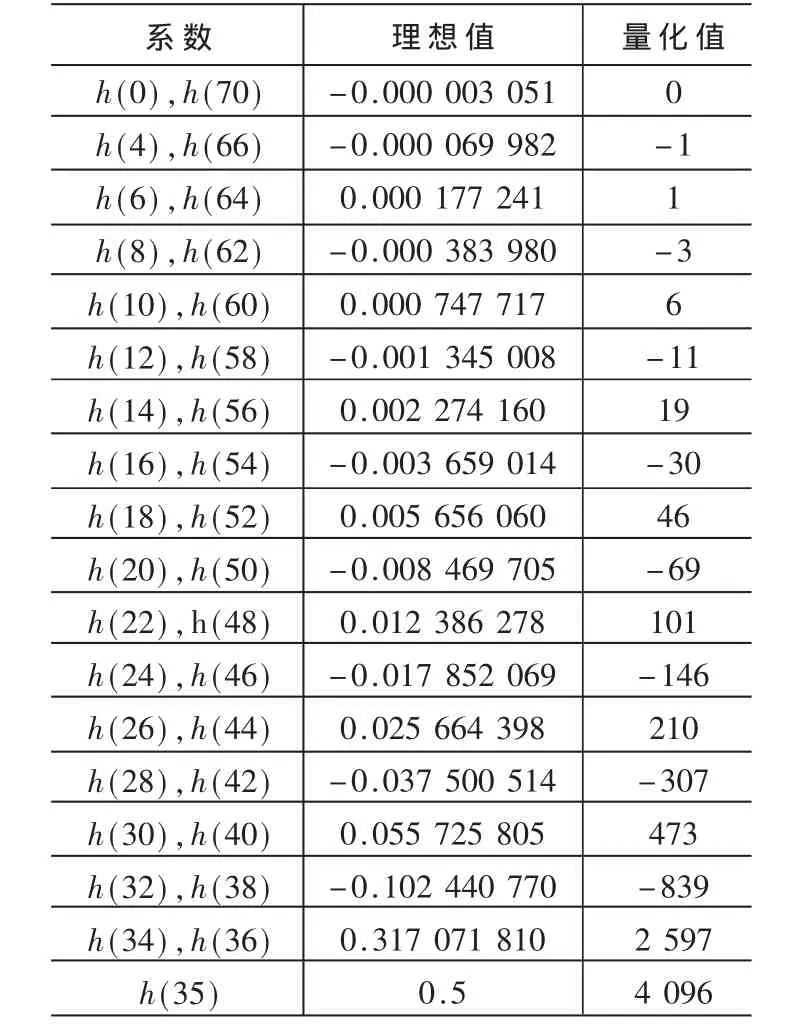
表2 半带滤波器2的系数

采用量化后的系数得到的滤波器的特性会有所变化，图7给出了第二级半带滤波器采用量化系数后幅频特性的变化。从图中可以看出其阻带波动变大，阻带衰减变小。

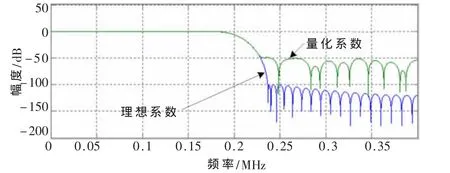
图7 采用量化系数和理想系数半带滤波器的幅频特性的变化

2.3 FIR补偿滤波器

由于梳状滤波器的通带内幅度响应一般有1 dB以上的下降，故在最后一级采用FIR线性相位滤波器来做基带补偿[9]。该补偿器没有抽取率的变化，因此可以不考虑在通带之外的频谱形状，只要不放大带外噪声就可以。设计过程如下：

(1)由性能指标和滤波器类型确定H(k)的模，使其满足|H(k)|=|H(N-k)|和 H(N/2)=0。

(2)根据滤波器的类型及频率采样法的特点确定H(k)的相角 θ(k)，使其 满足 θ(k)=-θ(N-k)和 θ(k)=-(N-1)/2×2π/N×k。

(3)由|H(k)|和 θ(k)构造出 H(k)，再经过逆变换求出冲激响应。

但根据以上步骤，对FIR补偿器进行设计，由于未采用优化手段，因此阶数较大，且效果不很明显。

本文设计的滤波器，采用了开关降频法能有效地减小芯片功耗，多相结构实现的半带滤波器大大减少了数据量，信噪比达98 dB，可以用于16 bit的过采样A/D转换器的后级部分。为减少功耗、降低运算量、提高分辨率等方面的高精度数据采集有重要意义。

[1]刘益成，罗维炳.信号处理与过抽样转换器[M].北京：电子工业出版社，1997.

[2]许波，林争辉.过采样转换器中数字滤波器设计[J].上海交通大学学报，2000(6).

[3]QUIQUEMPOIX V，BELLINI G.Digital decimation filter[P].US， 2004： 6， 233， 788.

[4]郝志刚.一种改进的适用于Sigma-Delta ADC的数字抽取滤波器[J].电子与信息学报，2010(4).

[5]LOSADS R，LYONS R.Reducing CIC filter complexity[J].IEEE Signal Process Magazine， 2006， 23(4)： 124-126.

[6]WAKERLY J F.著.数字设计原理与实践[M].林生，等译.北京：机械工业出版社，2004.

[7]CROCHIERE R E，RABINER L R.Multirate digital signal processing[M].Prentice Hall，1998.

[8]KUO S M，LEE B H著.实时数字信号处理[M].卢伯英译.北京：中国铁道出版社，2005.

[9]楼顺天.基于 Matlab的系统分析与设计[M].西安：西安电子科技大学出版社，2005.