决策树ID3算法研究及其优化

武献宇 ，王建芬 ，谢金龙

(1.湖南现代物流职业技术学院，湖南 长沙 410131；2.长沙医学院，湖南 长沙 410131)

分类是一种非常重要的数据挖掘方法，也是数据挖掘领域中被广泛研究的课题。决策树分类方法是一种重要的分类方法，它是以信息论为基础对数据进行分类的一种数据挖掘方法。决策树生成后成为一个类似流程图的树形结构，其中树的每个内部结点代表一个属性的测试，分枝代表测试结果，叶结点则代表一个类或类的分布，最终可生成一组规则。相对其他数据挖掘方法而言，决策树分类方法因简单、直观、准确率高且应用价值高等优点在数据挖掘及数据分析中得到了广泛应用。

1 决策树分类过程

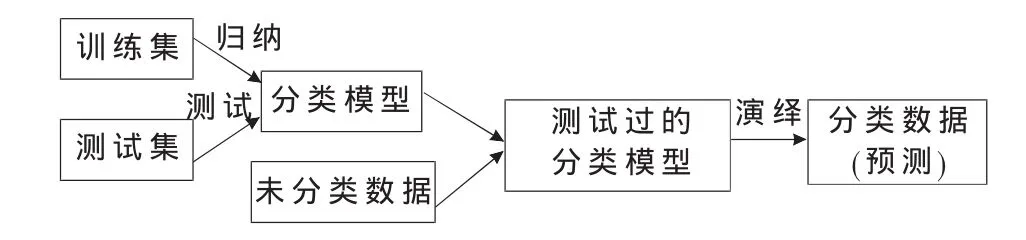
图1 决策树分类过程图

决策树的分类过程也就是决策树分类模型(简称决策树)的生成过程，如图1所示。从图中可知决策树分类的建立过程与用决策树分类模型进行预测的过程实际上是一种归纳-演绎过程。其中，由已分类数据得到决策树分类模型的过程称归纳过程，用决策树分类模型对未分类数据进行分类的过程称为演绎过程。需要强调的是：由训练集得到分类模型必须经过测试集测试达到一定要求才能用于预测。

2 ID3算法

2.1 ID3算法的理论基础

ID3算法的理论依据为：

设 E=F1×F2×…×Fn是 n 维有穷向量空间，Fj是有穷离散符号集，E 中的元素 e=＜V1，V2， …，Vn＞称为例子，其中 Vj∈Fj，j=1，2，…，n。设 PE 和 NE 是 E 的两个例子集，分别叫正例集和反例集。

假设向量空间E中的正例集PE和反例集NE的大小分别为p和n。ID3算法是基于如下两种假设：

(1)向量空间E上的一棵正确决策树对任意例子的分类概率同E中的正反例的概率一致。

(2)一棵决策树对一例子做出正确类别判断所需的信息量为:

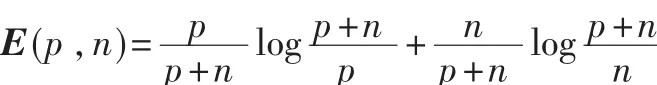
如果以属性A作为决策树的根，A具有V个值{V1，V2，V3，…，Vv}，它们将 E 分成 V 个子集{E1，E2，…，Ev}，假设 Ei中含有 pi个正例和 ni个反例，则子集Ei所需的期望信息是 E(pi，ni)，以属性 A为根的期望熵为：

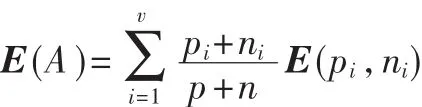
因此，以A为根的信息增益是：

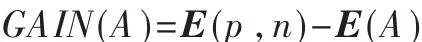
信息增益是不确定性的消除，也就是接收端所获得的信息量。

2.2 ID3算法多值偏向性分析

首先，设A是某训练样本集的一个属性，它的取值为 A1，A2，…，An，创建另外一个新属性 A′，它与属性 A唯一的区别：其中一个已知值 An分解为两个值 A′n和A′n+1，其余值和A中的完全一样，假设原来 n个值已经提供足够的信息使分类正确进行，很明显，则属性A′相对于A没有任何作用。但如果按照Qulnina的标准，属性A′应当优先于属性A选取。

综上所知，把ID3算法分别作用在属性A和属性A′上，如果属性选取标准在属性A′上的取值恒大于在属性A上的取值，则说明该算法在建树过程中具有多值偏向；如果属性选取标准在属性A′上的取值与在属性A上的取值没有确定的大小关系，则说明该决策树算法在建树过程中不具有多值偏向性。

2.3 ID3算法的缺点

(1)ID3算法往往偏向于选择取值较多的属性，而在很多情况下取值较多的属性并不总是最重要的属性，即按照使熵值最小的原则被ID3算法列为应该首先判断的属性在现实情况中却并不一定非常重要。例如:在银行客户分析中，姓名属性取值多，却不能从中得到任何信息。

(2)ID3算法不能处理具有连续值的属性，也不能处理具有缺失数据的属性。

(3)用互信息作为选择属性的标准存在一个假设，即训练子集中的正、反例的比例应与实际问题领域中正、反例的比例一致。一般情况很难保证这两者的比例一致，这样计算训练集的互信息就会存在偏差。

(4)在建造决策树时，每个结点仅含一个属性，是一种单变元的算法，致使生成的决策树结点之间的相关性不够强。虽然在一棵树上连在一起，但联系还是松散的。

(5)ID3算法虽然理论清晰，但计算比较复杂，在学习和训练数据集的过程中机器内存占用率比较大，耗费资源。

决策树ID3算法是一个很有实用价值的示例学习算法，它的基础理论清晰，算法比较简单，学习能力较强，适于处理大规模的学习问题，是数据挖掘和知识发现领域中的一个很好的范例，为后来各学者提出优化算法奠定了理论基础。表1是一个经典的训练集。

表1 天气数据库训练数据集

由ID3算法递归建树得到一棵决策树如图2所示。

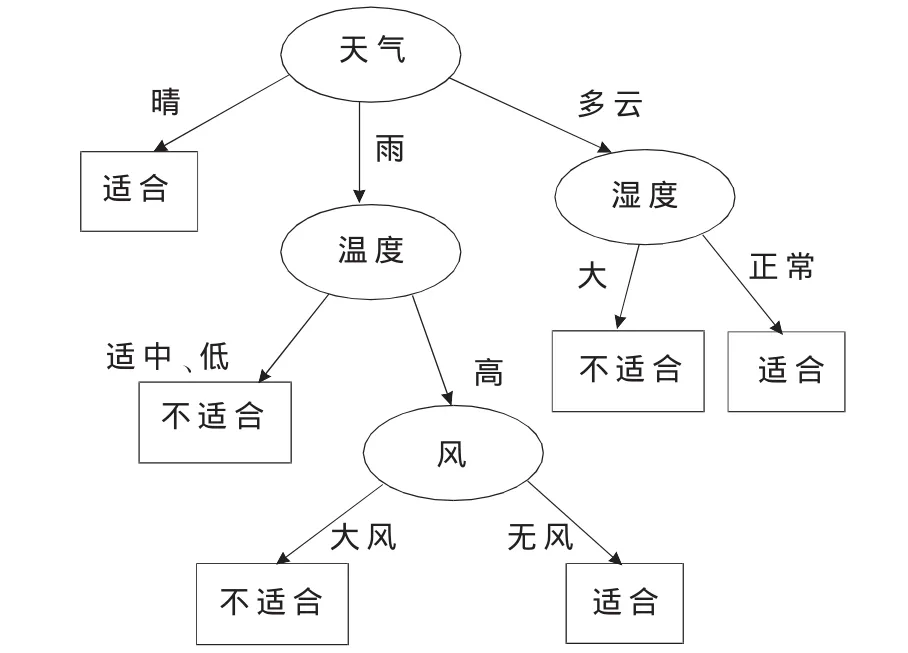
图2 ID3算法所生成的决策树

3 ID3算法优化的探讨

ID3算法在选择分裂属性时，往往偏向于选择取值较多的属性，然而在很多情况下取值较多的属性并不总是最重要的属性，这会造成生成的决策树的预测结果与实际偏离较大，针对这一弊端，本文提出以下改进思路：

(1)引入分支信息熵的概念。对于所有属性，任取属性A，计算A属性的各分支子集的信息熵，在每个分支子集中找出最小信息熵，并计算其和，比较大小，选择其最小值作为待选择的最优属性。

(2)引入属性优先的概念。不同的属性对于分类或决策有着不同的重要程度，这种重要程度可在辅助知识的基础上事先加以假设，给每个属性都赋予一个权值，其大小为(0，1)中的某个值。通过属性优先法，降低非重要属性的标注，提高重要属性的标注。

4 实例分析

仍以表1为例，分别计算其H(A)的值。在此通过反复测试，天气的属性优先权值为0.95，风的属性优先权值为0.35，其余两个的属性优先权值都为0。

(1)确定根结点

选取天气属性作为测试属性，天气为多云时，信息熵为：

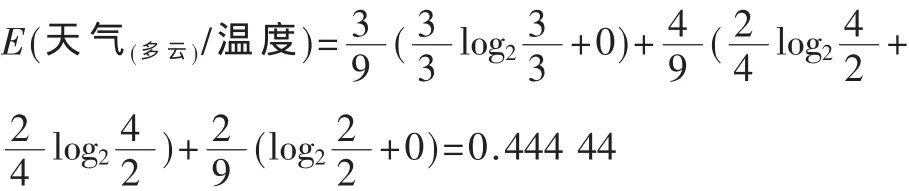
同理 E(天气(多云)/湿度)=0，E(天气(多云)/风)=0.972 77

从上面的计算可知，天气为多云时的最小信息熵为0。

当天气为晴时，由于此时对应的类别全部为适合打高尔夫球，所以信息熵都为0。

当天气为雨时的信息熵为：

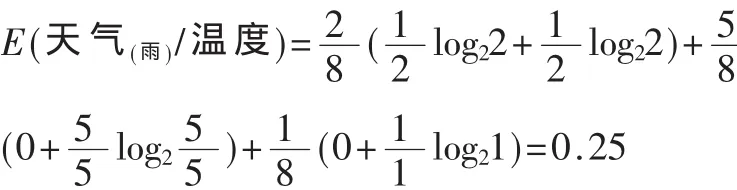
同 理 E(天 气(雨)/湿 度)=0.451 21，E(天 气(雨)/风 )=0.344 36

从上面的计算可知，天气为雨时的最小信息熵为0.25。

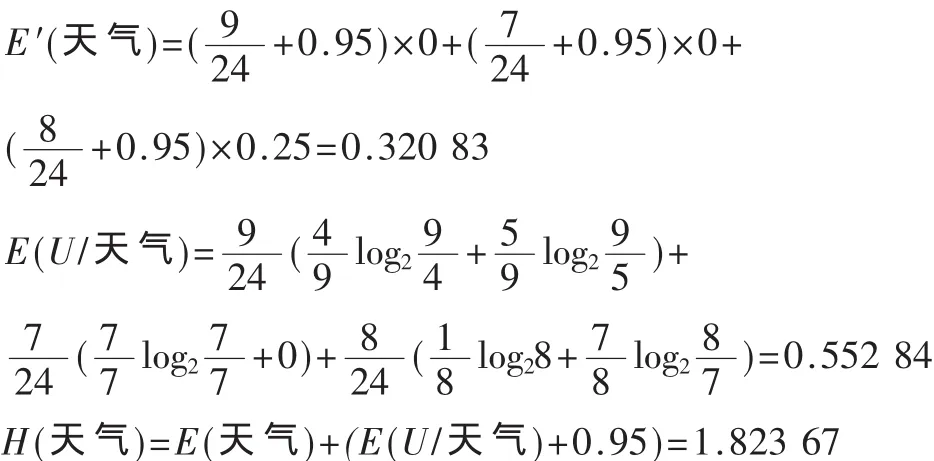
同 理 H(温 度)=1.083 83，H(湿 度)=1.068 7，H(风)=2.775 54

根据算法步骤(6)，选择值H(A)为最小的作为候选属性，所以此时应选择湿度作为根结点。在24个训练集中对湿度的2个取值进行分枝，2个分枝对应2个子集，分别为：

F1={1，2，3，4，5，6，7，13，14，21，22，24}(湿度为高对应)

F2={8，9，10，11，12，15，16，17，18，19，20，23}(湿度为正常对应)

(2)确定分支结点

计算F1分支子集：

H(温度)=0.908 05，H(天气)=0.95，H(风)=1.554 56

选择H(A)值为最小的作为候选属性，所以此时应选择温度作为湿度为大的下一级结点。在湿度为大的12个训练集中对温度的3个取值进行分枝，3个分枝对应3个子集，由于温度为低的子集不存在，所以此时也只有2个子集，分别为：

F11={1，2，3，4，5}(湿度为大且温度为高对应)

F12={6，7，13，14，21，22，24}(湿度为大且温度为适中对应)

同理，对于F2分支子集：

H(温度)=0.863 71，H(天气)=1.250 8，H(风)=1.554 6

选择H(A)值最小的作为候选属性，所以此时应选择温度作为湿度为正常的下一级结点。在湿度为正常的12个训练集中对温度的3个取值进行分枝，3个分枝对应3个子集，分别为：

F21={8，10，23}(湿度为正常且温度为高对应)

F22={17，18，19，20}(湿度为正常且温度为适中对应)

F23={9，11，12，15，16}(湿度为正常且温度为低对应)

继续对 F11，F12，F21，F22，F23等分支子集采用此优化算法递归建树，经过合并和简化后得到的决策树如图3所示。

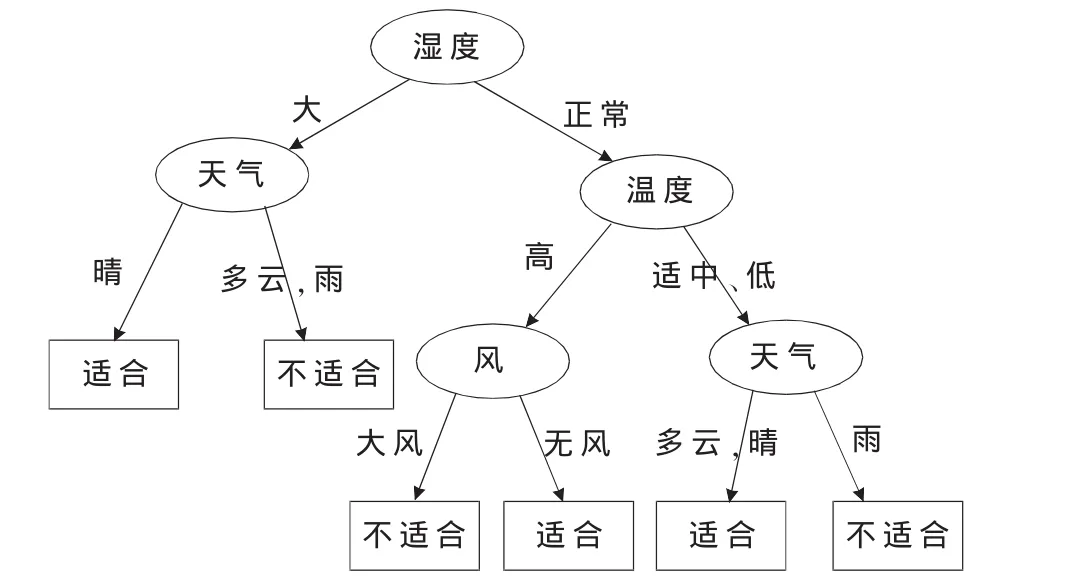
图3 优化算法所生成的决策树

通过比较ID3算法和本文所提出的组合优化算法所生成的决策树可知，组合优化算法的改进为：

(1)从本实例所生成的决策树的形态来看，改进后的算法生成的是一棵二叉树，而ID3算法生成的是多叉树，简化了决策问题处理的复杂度。

(2)引入了分支信息熵和属性优先的概念，用条件熵、分支信息熵与属性优先三者相结合来选择分裂属性。从本实例来看，根结点选择湿度而未选择属性值最多的天气，所以本优化算法确实能克服传统ID3算法的多值偏向性。

[1]安淑芝.数据仓库与数据挖掘[M].北京：清华大学出版社，2005：104-107.

[2]史忠植.知识发现[M].北京：清华大学出版社，2002：23-37.

[3]徐洁磐.数据仓库与决策支持系统[M].北京：科学出版社，2005：77-86.

[4]路红梅.基于决策树的经典算法综述[J].宿州学院学报，2007(4)：91-95.

[5]韩慧.数据挖掘中决策树算法的最新进展[J].计算机应用研究，2004(12)：5-8.

[6]KANTARDZIC M.Data mining concepts， models， methods，and algorithms[M].北京：清华大学出版社，2003：120-136.

[7]OLARU C，WEHENKEL L.A complete fuzzy decision tree technique[J].Fuzzy Sets and Systems， 2003，138(2)：221-254.

[8]AITKENHEAD M J.Aco-evolving decision tree classification method[J].Expert System with Application， 2008(34)：18-25.

[9]Norio Takeoka.Subjective probability over a subjective decision tree[J].Journal of Economic Theory，2007(136):536-571.