小生境遗传模糊PID控制在皮带秤中的应用

赵国强，张 鹏，孙红艳

(辽宁工程技术大学 电气控制与工程学院，辽宁 葫芦岛 125105)

配料皮带秤广泛应用于物流、煤矿、冶金、水泥等行业物料配比和称重。在配比中保持流量的恒定才能达到专业要求的配料比。通过称重传感器测得物料重量，由测速传感器测得皮带速度，并通过乘法处理得到瞬时流量。与设定值进行比较，从而控制电机速度来控制流量。由于配料皮带秤流量控制系统的非线性、滞后性以及数学模型的难以建立，所以采用模糊PID控制方法。而传统模糊PID定常控制，造成控制速度缓慢、收敛效率低。由于现场环境的变化和系统参数的变化，采用自适应模糊控制，融合改进的小生境遗传算法，可以更好地实时在线优化参数，克服了寻优缓慢和早熟收敛的缺点，使得进化速度加快，有效提高了优化能力，控制速度和效率都得到改善。

1 模糊PID控制

工业现场中，被控对象随着负荷的变化或干扰因素造成参数发生改变，并影响控制过程中各种信号量及评价指标不易定量表示，采用模糊自适应PID控制，在线辨识对象的特征参数，实时改变控制策略，通过模糊原理把相关参数模糊化，运用模糊推理进行模糊决策，共同实现PID参数的最佳调整。模糊PID控制[1]结构如图1所示。

图1 模糊PID控制结构图

PID模糊自适应是找出 3个 PID参数 kp、ki、kd与 e、ec之间的模糊关系。通过不断检测e、ec来实时调整这3个参数。

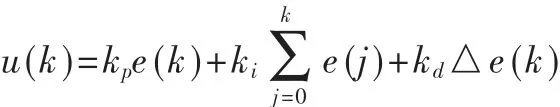
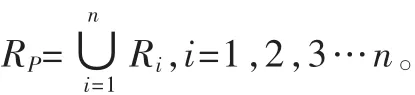
在模糊PID控制中引入遗传算法，通过选择、交叉、变异，得到全局最优解，将PID参数进一步优化。

2 遗传算法

2.1 基本遗传算法的简介

基本遗传算法[3]只使用选择算子、交叉算子和变异算子这3种基本遗传算子。其构成要素有：染色体编码方法、个体适应度评价、遗传算子、基本遗传算法的运行参数。其中，基本遗传算法使用3种遗传算子：选择运算使用比例选择算子；交叉运算使用单点交叉算子；变异运算使用基本位变异算子或均匀变异算子。

在用遗传算法求解具体问题时，经常是只能找到个别的几个最优解，甚至往往得到的是局部最优解，但有时希望优化算法能够找出问题的所有最优解，包括局部最优解和全局最优解，而基本遗传算法对此无能为力。既然为遗传算法模拟对象的生物都有其特定的生存环境，那么借鉴此概念，可以让遗传算法中的个体在一个特定的生存环境中进化，即在遗传算法中引入小生境技术，从而解决这类问题，以找出更多的最优解。

2.2 小生境技术

生物学中，小生境(Niche)[4]是指特定环境下的一种生存环境。生物在其进化过程中，一般总是与自己相同的物种生活在一起，共同繁衍后代，它们也都是在某一特定的地理区域中生存。小生境技术就是将每一代遗传个体分成若干类，每个类中选出若干适应度较大的个体作为一个类的优秀代表组成一个种群，再在种群中以及不同的种群间通过杂交、变异产生新一代个体群。可以更好地保持物种的多样性，使优良算子得到更好地利用，提高群体的整体搜索性和收敛效率，有利于最优解的产生。

3 改进的小生境遗传算法的优化原理

遗传算法的一般步骤如下[5]：

(1)确定决策的变量及约束条件；

(2)建立优化模型；

(3)确定可行解染色体的编码以及解码方法；

(4)确定个体适应度函数；

(5)设计遗传算子；

(6)确定有关运行参数。

传统遗传算法参数固定，交叉概率和变异概率随着遗传代数增加不发生变化，当种群中染色体差异较大时，应该增加交叉概率而相应地减少变异概率，以加快收敛速度；差异较小时，则反之，防止过早的进入局部最优。本文采用改进的小生境遗传算法，其中主要对遗传算子进行了改进，采用了改进的自适应交叉、变异概率来实时调整交叉、变异算子，加快寻优速度和提高全局优化能力。

3.1 全局变量的设定

种群数目M、最大遗传代数MAXGEN、常数等。

3.2 染色体编码

PID 控制参数 kp、ki、kd以及 e、ec 是寻优的参数，为了满足多维、高精度的要求，采用浮点编码方法，就是用某一范围内的一个浮点数来表示个体的每个基因值，个体的编码长度取决于决策变量的个数。

3.3 初始种群及小生境子群体的产生

运用小生境技术将每一代遗传个体分成若干类，每个类中选出若干适应度较大的个体作为一个类的优秀代表组成一个种群，再在种群中以及不同的种群间通过杂交、变异产生新一代个体群。初始群体先按经验选取一组参数，然后在这组参数的周围进行设计，大大减小了初始寻优的盲目性，节约计算量。

3.4 确定个体适应度函数

衡量一个控制系统的指标有3个方面：稳定性、准确性、快速性。 从寻优参数 kp、ki、kd以及 e和 ec可以看出稳定性与准确性。从上升时间可以看出系统的快速性。上升时间越短，控制得越快。设计的适应度函数必须要满足参数间很好的联系，因此性能指标函数为[6]：

w1，w2为权值，tu为上升时间。适应度函数f=1/J。

3.5 遗传算子的构成及改进

针对传统的遗传算法算子参数固定，容易造成早熟现象和局部最优的缺点，本文采用自适应遗传算法算子在线调整参数，使得寻优速度加快、全局寻优能力加强。另外将小生境技术引入自适应遗传算法，通过阈值实时控制子群规模，使得搜索能力和优化能力得到更大的提高。基本遗传算子包括：选择算子、交叉算子、变异算子。

3.5.1 选择算子的改进

本文改进选择2种选择算子，在整个群体中希望最好的个体要尽可能保存到下一代，采用最优保存策略，适应度高的个体不参加交叉和变异运算，用它来替换掉本代群体中经过交叉、变异等遗传操作后产生的适应度最低的个体。通过小生境技术将整个群体划分成若干个小生境，采用(μ+λ)选择机制，是进化算法选择机制中选择压最高的一种。当在种群中进行随机配对的交叉操作时，(μ+λ)选择机制能产生最快的局部收敛速度。(μ+λ)选择策略是指在μ个父代个体和由这μ个个体交叉产生的λ个子个体中选择μ个最佳个体。通过2种选择算子，使群体间适应度差异变小，适应度高的个体遗传到下一代的概率增加。

3.5.2 交叉概率与变异概率的改进

4 改进的小生境遗传模糊控制在电子皮带秤中的应用

图2 传统遗传算法进化过程

图3 改进的小生境遗传进化过程

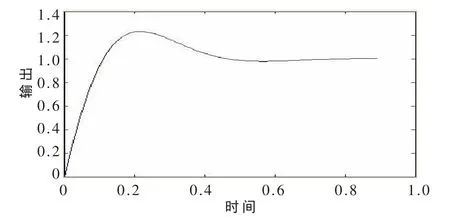
图4 传统的遗传PID控制响应时间图

图5 改进的小生境遗传模糊控制响应时间图

本文采用小生境遗传算法，并且改进了交叉、变异概率公式，自适应调节了交叉、变异算子，改善了传统遗传算法的早熟现象和局部收敛僵局、以及后期收敛速度慢的缺点，经仿真表明收敛效率提高、速度加快，得到更优的全局最优解。将改进的小生境遗传算法结合模糊PID控制理论应用于电子皮带秤中，对调速电机速度进行控制，进而调节物料的流量，经仿真表明达到满意的结果。

[1]刘曙光，魏俊民.模糊控制技术[M].北京：中国纺织出版社，2001.

[2]陶永华.新型 PID控制及其应用[M].北京：机械工业出版社，2002.

[3]GOLDBERG D E.Genetic algorithms in search，optimization and machine learning[M].Addison-Wesley， 1989.

[4]周明，孙树栋.遗传算法原理及应用[M].北京：国防工业出版社，2000.

[5]郭嗣综，陈刚.信息科学中的软计算方法[M].沈阳：东北大学出版社，2001.

[6]YUAN Xiao Hui， CAO Ling Xia， LIANG Zheng.Adaptive genetic algorithm with the criterion of premature convergence[J].Journal of Southeast University[J].2003，19(1)：40-43.

[7]李士勇.模糊控制.神经控制和智能控制[M].哈尔滨：哈尔滨工业出版社，1996.

[8]SRINVAS M，PATNAIK L M.Adaptive probabili-ties of crossover and mutation in genetic algorithms[C].In：IEEE Trans on Systems， Man and Cybernetics， 1994：24(4).

[9]刘金琨.先进 PID控制 MATLAB仿真[M].北京：电子工业出版社，2004.